组合数学 完整版

一、组合数学介绍

1、组合数学用于解决2种问题

A、某种结构的存在性

B、某种结构的数量

二、乘法法则

定义

假设一个任务，可以被分解成两个任务，完成任务1有n1种方式。完成任务一之后，完成任务二有n2种方式。那么完成总任务的方式n1*n2种。该定理可以推广到分解为多个任务。

例题

1、有四个字母，分别ABCD，有两个数，他们分别要选四个数，问一共有几种选法

这道题我们可以这样解：

设两个数分别是1和2，1可以选A，2可以选ABCD如下图

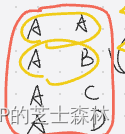
1还可以选择B，那2可以选ABCD如下图

以此类推所以一共有 种

1. 又四个字母，分别ABCD，有两个数（1和2），他们分别要选四个数，但是2要比1选的字母小（顺序靠后），问一共有几种选法

这道题我们可以这样解：

1选则了A，那2就要选BCD，如下图

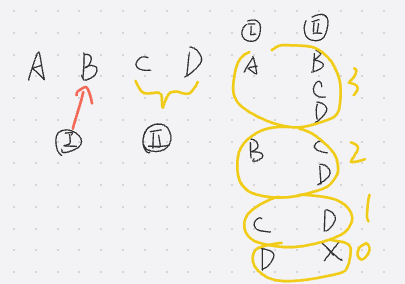
根据上图，所以得出结果为

三、加法法则

定义

设事件 A 有 m 种产生方式， 事件 B 有n 种产生方式，则当 A 与 B 产生的方式不重叠时，“事件 A 或 B 之一” 有m+n 种产生方式。事件 A1有 p1种产生方式， 事件 A2 有p2种产生方式……事件 Ak 有 pk种产生的方式，则当其中任何两个事件产生的方式都不重叠时，“事件 A1 或A2或… Ak” 有 p1+p2+…+pk种产生的方式。如下图

例题

这个题我们可以这样解：

密码为6位，7位，8位，所以这是三种不同的类别，而题目又说密码的内容包括大写字母和数字，所以，每个数位都有36种选择，则密码是6位的一共就有种，7位的有种，8位有种，因为这是三种不同的分类，所以要加起来一共就是种可能性。

易错题

这个题不是运用加法法则，而是乘法法则，因为这是一整串密码，不是分开始的，因此这道题的答案是种可能

四、 减法法则（容斥原理）

定义

集合：若干个元素组成的无序的聚集（包括0，0个元素代表的是空集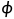）若干个元素指的是集合里面元素的个数，它可以是3个，10个，100个，也就是个，集合包括N(自然数集）、R（实数集，实数集指有理数集和无理数集）、Z（整数集），或者是集合里面还有集合，如下图

这个集合的元素个数是2，而不是4。

在集合中，不能出现相同的元素，如{1，1，1，2}这样的集合是不合法的。但是像{1，1，2}和{1，2，1}这两个集合是相同的，也就是说在集合内，只要元素相同，这个集合就是一样的。

集合的运算

1. 交集（∩）

定义

两个集合的交集：两个集合中相同的元素组成的集合

2. 并集（∪）

定义

两个集合的并集：由在两个集合中其中一个或两个里面出现的元素组成的集合

A和B的并集：存在于A中元素或存在与B中的元素组成的集合

3. 模（| |）

定义

集合的模：集合中元素的个数

4. 公式总结

五、鸽巢原理

A、狭义鸽巢原理

定义：如果有K+1个或者更多的物品放到K个盒子里。

B、广义鸽巢原理

定义：N个物品放到M个盒子里，一定有一个盒子物品数量>=(N/M)(向上取整）

见鸽巢原理

六、组合数学题目

1. 题目

（1）N个物品分成不同的K组（要求每组不能为空）

视频讲解