组合数学学习笔记

最新推荐文章于 2023-03-16 22:40:05 发布

eazo

最新推荐文章于 2023-03-16 22:40:05 发布

阅读量1k

点赞数 1

分类专栏：组合数学

组合数学专栏收录该内容

5 篇文章 0 订阅

订阅专栏

排列组合基础

加法原理：S = S1 ∪S2 ∪···∪Sm, Si ∩ Sj = ∅ 每种方案
|S| = |S1|+|S2|+···+|Sm|

乘法原理：S = P ×Q ⇒|S| = |P|×|Q| 每个步骤

例如从甲地到乙地有两条路可走，从乙到丙地有三条路可走，又从甲地不经乙地直达丙地有三条路可走，问从甲地到丙地的不同走法有几种？
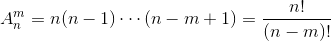
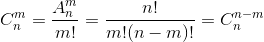
在这里插入图片描述
长度为 n 的排列数 n! = 1·2···n
n 个人中选出 k 个排成一队有序的方案数
P(n , k) = n · (n - 1) ··· (n - k + 1) = n! / (n - k )!
n 个人中选出 k 个组成一组的方案数
C(n , k) = n · (n - 1) ··· (n - k + 1) = n! / (n – k)! / k! = C(n ,n-k) (0<= k <= n)
n个人分入k个班，每个班至少一个人的方案数 C(n-1,k-1) （隔板法）
n个人分成k个班，第 i 个班恰好 ai 个人的方案数（乘法原理）
C(n,a1) · C(n-a1,a2) ··· C(ak-1+ak,ak-1) · C(ak , ak) = n! / (a1! · a2! ··· ak!)

在这里插入图片描述

Lucas 定理

对于非负整数n,m 和质数 p 有
C(n , m) = ||C(ni , mi) (mod p)
其中 ni 和 mi 分别为 n 和 m 的p进制表示的系数
若 n<m 则认为 C(n , m) = 0

Lucas 证明

费马小定理 x^(p-1) ≡ 1 ( mod p )
（1+x）^p ≡ （1+x^p）（mod p）
（1+x）ⁿ（mod p）=（1+x）^（n/p*p） *（1+x）^(n % p）^（mod p）
（1+x）ⁿ（mod p）= （1+x^p）^（n/p） * （1+x）^（n%p）（mod p）
二项式展开

Lucas 代码实现

方法一

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N=1e5+10;
const int mod=1e9+7;
int fac[N],fnv[N];
ll C(int x,int y)
{
    if(x<y) return 0;
    return 1ll*fac[x]*fnv[y]%mod*fnv[x-y]%mod;
}
ll quickmod(ll x,ll y)
{
    ll ans=1;
    for(;y;y>>=1)
    {
        if(y&1) ans=ans*x%mod;
        x=x*x%mod;
    }
    return ans;
}
int main()
{
    fac[0]=1;
    for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;
    fnv[N-1]=quickmod(fac[N-1],mod-2);
    for(int i=N-2;i>=0;i--) fnv[i]=1ll*fnv[i+1]*(i+1)%mod;
    cout<<C(5,3)<<endl;
    return 0;
}

方法二

#include <iostream>
#include <cstdio>
using namespace std;
typedef long long ll;
const int N=1e5+10;
const int mod=1e9+7;
int fac[N],fnv[N],inv[N];
ll C(int x,int y)
{
    if(x<y) return 0;
    return 1ll*fac[x]*fnv[y]%mod*fnv[x-y]%mod;
}
ll lucas(int n,int m)
{
    if(n<m) return 0;
    if(n<mod && m<mod) return C(n,m);
    return lucas(n/mod,m/mod)*C(n%mod,m%mod)%mod;
}
int main()
{
    fac[0]=1;
    for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;
    inv[1]=1;
    for(int i=2;i<N;i++) inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
    fnv[0]=1;
    for(int i=1;i<N;i++) fnv[i]=1ll*inv[i]*fnv[i-1]%mod;
    cout<<lucas(5,3)<<endl;
    return 0;
}

鸽巢定理（抽屉原理）与Ramsey定理

第一抽屉原理：

1.把多于n+1个的物体放到n个抽屉里，则至少有一个抽屉里的东西不少于两件。

2.把多余mn+1（n!=0）个的物体放到n个抽屉里，则至少有一个抽屉里有不少于（m+1）的物体。

3.把无穷多件物体放入n个抽屉，则至少有一个抽屉里有无穷个物体。

第二抽屉原理：

把（mn-1）个物体放入n个抽屉里，其中必有一个抽屉中至多有（m-1）个物体
（例如，将3*5-1=14个物体放入5个抽屉中，则必定有一个抽屉中的物体数少于等于3-1=2）

最差原则：

即考虑所有可能情况中，最不利于某件事情发生的情况。

例如，有300人到招聘会求职，其中软件设计有100人，市场营销有80人，财务管理有7人，人力资源管理有50人。那么至少有多少人找到工作才能保证一定有70人找的工作专业相同呢？

此时我们考虑的最差情况为：软件设计、市场营销和财务管理各录取69人，人力资源管理的50人全部录取，则此时再录取1人就能保证有70人找到的工作专业相同。

因此至少需要69*3+50+1=258人

例：

如果 n + 1 个鸽手分别说它在前 n 天比赛的某一天要鸽，那么至少有一天包含两个及更多的鸽手要鸽。

如果 n 个鸽手分别说它在前 n 天比赛的某一天要鸽，且每一天至少有一个鸽手要鸽，那么每一天恰好有一个鸽手要鸽。

1.从 1,2,··· ,2n 中选出 n + 1 个整数，一定存在一个数比另一个数大 1。
2.从 1,2,··· ,2n 中选出 n + 1 个整数，一定存在一个数是另一个数的因子。
3.在边长为 n 的等边三角形内选出 5 个点，一定存在一个点到另一个点距离不超过 n/2。

Ramsey 定理：

Ramsey定理

定义 Kn 表示 n 个点的完全图，对于给定的 n 和 m，存在一个最小的正整数 p 使得将 Kp 的边分别染上红色或蓝色后，一定存在一个 Kn 子图是红色或者一个 Km 子图是红色，并且对于更大的任意 p 都成立，这样的 p 记作 r(n,m)。

在这里插入图片描述
对于任意 6 个人，要么有 3 个人两两认识，要么有 3 个人两两不认识。考虑第一个人至少认识或不认识的那 3 个人是否认识

目前 ICPC 中只需要了解 r(1,m) = 1, r(2,m) = m, r(3,3) = 6, r(4,4) = 18。

例题

CCPC 2016 Changchun G Instability
给定一个 n 点 m 边的无向图 (n ≤ 50)，问有多少点集满足要么存在三个点两两相连，要么存在三个点两两不相连

思路：
根据Ramsey 定理，可得r(3,3)=6 ，所以6元及以上集合必然有三元完全子图。只需暴力跑一遍5元集以下即可

代码实现

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=105;
const int mod=1e9+7;
int fac[N],fnv[N];
int n,m;
int rec[10];
bool groud[N][N];
ll ans;
ll C(int x,int y)
{
    if(x<y) return 0;
    return 1ll*fac[x]*fnv[y]%mod*fnv[x-y]%mod;
}
ll quickmod(ll x,ll y)
{
    ll ans=1;
    for(;y;y>>=1)
    {
        if(y&1) ans=ans*x%mod;
        x=x*x%mod;
    }
    return ans;
}
void getf()
{
    fac[0]=1;
    for(int i=1;i<N;i++) fac[i]=1ll*fac[i-1]*i%mod;
    fnv[N-1]=quickmod(fac[N-1],mod-2);
    for(int i=N-2;i>=0;i--) fnv[i]=1ll*fnv[i+1]*(i+1)%mod;
}
void dfs(int x,int y)
{
    if(x==6) return;
    for(int i=y+1;i<=n;i++)
    {
        rec[x]=i;
        if(x>=3)
        {
            bool flag=false;
            for(int p1=1;p1<x-1;p1++)
            {
                for(int p2=p1+1;p2<x;p2++)
                {
                    for(int p3=p2+1;p3<=x;p3++)
                    {
                        if(groud[rec[p1]][rec[p2]] && groud[rec[p2]][rec[p3]]&& groud[rec[p3]][rec[p1]])
                        {
                            ans++;
                            flag=true;
                            break;
                        }
                        else if(!groud[rec[p1]][rec[p2]] && !groud[rec[p2]][rec[p3]]&& !groud[rec[p3]][rec[p1]])
                        {
                            ans++;
                            flag=true;
                            break;
                        }
                    }
                    if(flag) break;
                }
                if(flag) break;
            }
        }
        dfs(x+1,i);
    }
}
int main()
{
    getf();
    int T;
    scanf("%d",&T);
    for(int no=1;no<=T;no++)
    {
        scanf("%d%d",&n,&m);
        memset(groud,false,sizeof(groud));
        int x,y;
        for(int i=0;i<m;i++)
        {
            scanf("%d%d",&x,&y);
            groud[x][y]=groud[y][x]=true;
        }
        ans=quickmod(2,n);
        for(ll i=0;i<=5;i++)
        {
            ans=(ans-C(n,i)+mod)%mod;
        }
        dfs(1,0);
        printf("Case #%d: %lld\n",no,ans);
    }
    return 0;
}

CCPC 2017 Online C Friend-Graph
如果一个队伍里有至少三个人两两认识或者至少三个人两两不认识，则这个队伍是不好的队伍。
给定一个有 n (n ≤ 3000) 个人的队伍以及相互认识关系，判断是否这个队伍不好

思路：同上

代码:

#include <iostream>
#include <cstdio>
#include <cstring>
using namespace std;
typedef long long ll;
const int N=3005;
bool member[N][N];
int n;
bool flag;
void dfs()
{
    for(int i=1;i<n-1;i++)
    {
        for(int j=i+1;j<n;j++)
        {
            for(int k=j+1;k<=n;k++)
            {
                if(member[i][j]&&member[i][k]&&member[j][k])
                {
                    flag=true;
                    break;
                }
                else if(!member[i][j]&&!member[i][k]&&!member[j][k])
                {
                    flag=true;
                    break;
                }
            }
            if(flag) break;
        }
        if(flag) break;
    }
}
int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
      flag=false;
      scanf("%d",&n);
      for(int i=1;i<n;i++)
      {
          for(int k=i+1;k<=n;k++)
          {
              int temp;
              scanf("%d",&temp);
              member[i][k]=member[k][i]=temp;
          }
      }
      if(n>5) printf("Bad Team!\n");
      else
      {
          dfs();
          if(flag) printf("Bad Team!\n");
          else printf("Great Team!\n");
      }
    }
    return 0;
}

容斥原理

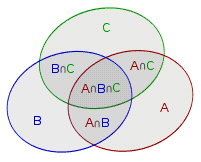
在这里插入图片描述
容斥原理是一种重要的组合数学方法，可以让你求解任意大小的集合，或者计算复合事件的概率。要计算几个集合并集的大小，我们要先将所有单个集合的大小计算出来，然后减去所有两个集合相交的部分，再加回所有三个集合相交的部分，再减去所有四个集合相交的部分，依此类推，一直计算到所有集合相交的部分。

在这里插入图片描述

卡特兰数

卡特兰数
卡特兰数是一种经典的组合数，经常出现在各种计算中，其前几项为 :

1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012,
742900, 2674440, 9694845, 35357670, 129644790, 477638700,
1767263190, 6564120420, 24466267020, 91482563640,
343059613650, 1289904147324, 4861946401452, …

公式 h(n) = h(0) * h(n-1)+h1h(n-2)+ …+h(n-1)h(0)
一般式 h(n) = C(2n,n)/(n+1)
另类递推公式：C(n)=C(n-1)((4*n-2)/(n+1));

推导考虑减掉不符合要求的01序列，建立对应关系

应用

长度为2*n的0 1序列，要求0的个数与1的个数相同，并且满足在任意位置，序列的前缀中0的个数不多于1的个数。

括号匹配

进出栈顺序

在圆上选择2n个点,将这些点成对连接起来，使得所得到的n条线段不相交的方法数

给定N个节点，能构成多少种形状不同的二叉树

第一类斯特林

表示将 n 个不同元素构成m个圆排列的数目
公式 s(n , m) = s(n-1 , m-1) + n*s(n-1 , m)
考虑第n个元素放哪
例题有n个仓库，每个仓库有两把钥匙，共2n把钥匙。同时又有n位官员。问如何放置钥匙使得所有官员都能够打开所有仓库？
将官员分成m组，每组能打开且只能打开本组的仓库

第二类斯特林数

表示将n个不同的元素拆分成m个集合的方案数
公式 s(n , m) = s(n-1 , m-1) + m*s(n-1 , m)
同理考虑第n个元素放哪

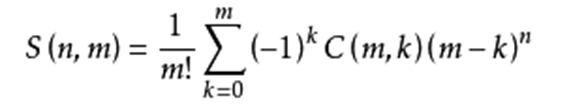
在这里插入图片描述
容斥原理

例题

n个不同的球，放入m个无区别的盒子，不允许盒子为空。
解=s(n,m)

n个不同的球，放入m个有区别的盒子，不允许盒子为空。
解=s(n,m)*m!

n个不同的球，放入m个无区别的盒子，允许盒子为空。
解=设k为空盒子的个数，进行枚举(k=0…m)
累加s(n,m-k)

n个不同的球，放入m个有区别的盒子，允许盒子为空。

二项式反演等众多反演
生成函数与图计数
Burnside引理与polya定理

eazo

关注

1
点赞
踩
7

收藏

觉得还不错? 一键收藏
0
评论
组合数学学习笔记

排列组合基础加法原理：S = S1 ∪S2 ∪···∪Sm, Si ∩ Sj = ∅ 每种方案|S| = |S1|+|S2|+···+|Sm|乘法原理：S = P ×Q ⇒|S| = |P|×|Q| 每个步骤例如从甲地到乙地有两条路可走，从乙到丙地有三条路可走，又从甲地不经乙地直达丙地有三条路可走，问从甲地到丙地的不同走法有几种？长度为 n 的排列数 n! = 1·2···nn...
复制链接

扫一扫