分治法就是吧一个大问题分成几个结构相同的子问题,再把子问题分解成更小的子问题.......
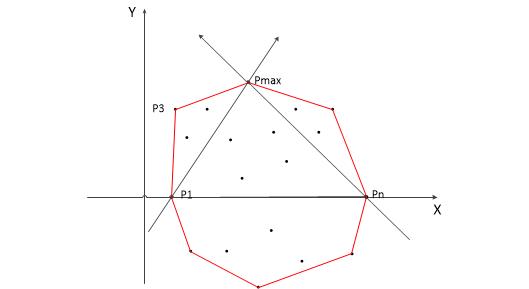
分治法解决凸包问题的大体思路就是,取横坐标最小的点p0和横坐标最大pn的点(这两个点一点在凸包上,这个仔细想想能想明白)然把这两个点连成一条直线,直线上面的半个凸包叫上凸包,直线下面的半个凸包叫下凸包,分别在上凸包和下凸包找出距离直线最大的点pmax,链接p1pmax和pnpmax如下图,又可以把上下两个凸包分解成更小的上凸包和下凸包,为什么说是更小的上凸包和下凸包,我们看下图,如果我们把p1pn这条线段看成是一条有向线段,那么下凸包在它的右方,上凸包在它的左方,以上凸包为例,连接p1pmax之后再找下一个pmax的时候我们肯定是要在p1pmax这条有向线段的左方进行查找,因此我们可以将p1pmax这条线段的左方看成一个更小的上凸包,同理,连接pnpmax我们要找到下一个pmax肯定要在pnpmax的右方查找,这就和下凸包的查找方式一样了,我们可以将它看成一个下凸包。
关于怎么判断点在直线的左方还是右方,假设有p1,p2,p3,三个点则有:
如果该式的值大于0,p3在p1p2形成直线的左侧,小于0在右侧,等于0在直线上。
现在我们思路有了接下来开始看代码吧
//这是三个点的叉乘(判断第三个点在直线的左方还是右方)
double multi(node p1, node p2, node p3)
{
return p1.x*p2.y+p3.x*p1.y+p2.x*p3.y-p3.x*p2.y-p2.x*p1.y-p1.x*p3.y;
}
/*
求p3点到p1p2直线的距离
*/
double dist(node p1, node p2, node p3)
{
return abs((p2.y-p1.y)*p3.x+(p1.x-p2.x)*p3.y+(p1.y-p2.y)*p1.x+(p2.x-p1.x)*p1.y)/sqrt(pow(p2.y-p1.y,2)+pow(p1.x-p2.x,2));
}/*
按x升序重载排序规则,如果x相同按照y升序
*/
bool cmp(node a, node b)
{
if(abs(a.x-b.x) <= eps)
return a.y < b.y;
return a.x < b.x;
}
/*
按照横坐标升序排序之后,下标为0的点和下标为n-1的点连线将凸包分成上下两个凸包
*/
void convex_hull(int n)
{
sort(p,p+n,cmp);
dhull(0,n-1);
uhull(0,n-1);
}
/*
求解下凸包,分界线为下标为x的点指向下标为y的点
*/
void dhull(int x, int y)
{
int i, j, l, r;
double dis = -1;
j = -1;
if(x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for(i = l + 1;i < r;i++)///无论是上凸包还是下凸包所要找的最远点的横坐标的最小值肯定不会小于p[l].x的最小值,最大值肯定不会大于p[r].x,而我们的点是按照横坐标升序的所以只需遍历(l,r)
{
if(multi(p[x],p[y],p[i]) <= 0)///下凸包所要找的最远点在p[x]p[y]这条有向线段的右侧( multi < 0),如果和p[x]p[y]共线且p[x]p[y]是凸包的一条边,那么肯定也在凸包边上,因为p[x]p[y]这条线段上的任意一点都在凸包上,所以要加=
{
if(dist(p[x],p[y],p[i]) > dis)///判断距离直线的距离
{
dis = dist(p[x],p[y],p[i]);
j = i;
}
}
}
if(j == -1)///未找到最远点那么这两个点是在凸包上直接相连的两个点
{
s[m++] = p[x];
return;
}
int uh, dh;
/*
关于怎么判断是上凸包还是下凸包我看他们的博客的代码都很乱不知道写的啥,按照我自己的思路就是p[x]p[y]是当前半个凸包的分界线,如果p[y]在p[x]p[j]的
右方,p[j]为pmax,那么下一个pmax肯定在p[x]p[j]的左方,p[y]p[j]的右方。
否则pmax在p[x]p[j]的右方,p[y]p[j]的左方。
这样就能直接判断哪个是上凸包,哪个是下凸包,想不明白的可以自己画个图看看
*/
if(multi(p[x],p[j],p[y]) < 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh,j);
uhull(uh,j);
}
/*
求解上凸包和求解下凸包的基本思路是一样的,差别就在于一个在左边找点,一个在右边找点,区分下一个上下凸包的时候也有点不同
*/
void uhull(int x, int y)
{
int i, j, l, r;
double dis = -1;
j = -1;
if(x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for(i = l + 1;i < r;i++)
{
if(multi(p[x],p[y],p[i]) >= 0)
{
if(dist(p[x],p[y],p[i]) > dis)
{
dis = dist(p[x],p[y],p[i]);
j = i;
}
}
}
if(j == -1)
{
s[m++] = p[y];
return;
}
int uh, dh;
/*
为什么下凸包这里没有加等于号这里要加等于号
看下面的图片吧
*/
if(multi(p[x],p[j],p[y]) <= 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh,j);
uhull(uh,j);
}
假设左图为上凸包上的边,右图为下凸包上的边
先看左图
p[x]p[y]左面已经没有点了,所以p[x]p[y]肯定是凸包上的两个点,但是有一个点p[j]与p[x]p[y]共线,如果题目让你找出凸包上的所有点,那么p[j]这个点是不能舍弃的,看图能看出来p[x]p[j]这个边是要归在上凸包里面的,如果归在下凸包就错了,但是再看右边那个p[x]p[j]是要归在下一个小凸包的下凸包里的,所以,在分下一个上下凸包的时候一个有“=”一个没有,是因为上下凸包,对于共线的这种情况分类不同。
分治法解决凸包问题的思路和代码都讲完了,那么接下来找个题练练手吧
题意:有n个点,现在要你用最少的材料修一个墙将n个点围起来,围墙距离每个点的距离不得小于l
求出围墙的最小周长
思路:如果直接围起来消耗最小肯定是一个凸包,但是有一个最小距离l,只要求出凸包的周长再加上以l为半径圆的周长就是围墙的最小周长,输出四舍五入其实printf它自动就是四舍五入的,如果交g++用%f,c++用%lf,poj就是这么坑...
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#define PI acos(-1.0)
#define eps 1e-9
using namespace std;
struct node
{
double x, y;
};
node p[1100], s[1100];
int m;
double multi(node p1, node p2, node p3);
bool cmp(node a, node b);
double dist(node p1, node p2, node p3);
double distd(node a, node b);
void convex_hull(int n);
void uhull(int x, int y);
void dhull(int x, int y);
int main()
{
int n, i;
double d;
m = 0;
cin>>n>>d;
for(i = 0;i < n;i++)
cin>>p[i].x>>p[i].y;
convex_hull(n);
double sum = 0;
//cout<<endl<<endl;
for(i = 0;i < m;i++)
{
//cout<<s[i].x<<','<<s[i].y<<endl;
sum += distd(s[i],s[(i+1)%m]);
}
printf("%.0lf\n",sum + 2 * PI * d);
return 0;
}
double dist(node p1, node p2, node p3)
{
return abs((p2.y-p1.y)*p3.x+(p1.x-p2.x)*p3.y+(p1.y-p2.y)*p1.x+(p2.x-p1.x)*p1.y)/sqrt(pow(p2.y-p1.y,2)+pow(p1.x-p2.x,2));
}
double multi(node p1, node p2, node p3)
{
return p1.x*p2.y+p3.x*p1.y+p2.x*p3.y-p3.x*p2.y-p2.x*p1.y-p1.x*p3.y;
}
bool cmp(node a, node b)
{
if(abs(a.x-b.x) <= eps)
return a.y < b.y;
return a.x < b.x;
}
double distd(node a, node b)
{
return sqrt(pow(a.x-b.x,2) + pow(a.y - b.y,2));
}
void convex_hull(int n)
{
sort(p,p+n,cmp);
dhull(0,n-1);
uhull(0,n-1);
}
void dhull(int x, int y)
{
int i, j, l, r;
double dis = -1;
j = -1;
if(x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for(i = l + 1;i < r;i++)
{
if(multi(p[x],p[y],p[i]) <= 0)
{
if(dist(p[x],p[y],p[i]) > dis)
{
dis = dist(p[x],p[y],p[i]);
j = i;
}
}
}
if(j == -1)
{
s[m++] = p[x];
return;
}
int uh, dh;
if(multi(p[x],p[j],p[y]) < 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh,j);
uhull(uh,j);
}
void uhull(int x, int y)
{
int i, j, l, r;
double dis = -1;
j = -1;
if(x <= y)
{
l = x;
r = y;
}
else
{
l = y;
r = x;
}
for(i = l + 1;i < r;i++)
{
if(multi(p[x],p[y],p[i]) >= 0)
{
if(dist(p[x],p[y],p[i]) > dis)
{
dis = dist(p[x],p[y],p[i]);
j = i;
}
}
}
if(j == -1)
{
s[m++] = p[y];
return;
}
int uh, dh;
if(multi(p[x],p[j],p[y]) <= 0)
{
uh = x;
dh = y;
}
else
{
uh = y;
dh = x;
}
dhull(dh,j);
uhull(uh,j);
}
最后在附上用Graham扫描法做这道题的代码
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <cmath>
#include <algorithm>
#define inf 0x3f3f3f3f
#define pi acos(-1.0)
#define eps 1e-9
using namespace std;
struct node
{
double x, y;
};
node p[1100];
node s[1100];
node minp;
int top;
bool equal(double x)
{
return abs(x-0) <= eps;
}
double multi(node p1, node p2, node p3)
{
return p1.x*p2.y+p3.x*p1.y+p2.x*p3.y-p3.x*p2.y-p2.x*p1.y-p1.x*p3.y;
}
double distence(node a, node b)
{
return sqrt((a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y));
}
bool cmp(node a, node b)
{
if(equal(multi(minp,a,b)))
return distence(minp,a) - distence(minp,b) < 0;
return multi(minp,a,b) > 0;
}
void convex_hull(int n)
{
sort(p,p+n,cmp);
s[0] = p[0];
s[1] = p[1];
top = 1;
for(int i = 2; i < n; i++)
{
while(multi(s[top-1],s[top],p[i]) < 0)
top--;
s[++top] = p[i];
}
}
int main()
{
int n, i;
double d, sum;
while(cin>>n>>d)
{
top = 0;
sum = 0;
minp.x = inf;
minp.y = inf;
for(i = 0; i < n; i++)
{
cin>>p[i].x>>p[i].y;
if(p[i].y < minp.y || (p[i].y == minp.y && p[i].x < minp.x))
{
minp.x = p[i].x;
minp.y = p[i].y;
}
}
convex_hull(n);
top++;
for(i = 1; i <= top; i++)
{
sum += distence(s[i%top],s[(i+1)%top]);
}
sum += 2.0*pi*d;
printf("%.0lf\n",sum);
}
return 0;
}
所以那种方法更简单心里还没点b-tree么?





















 3378
3378

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








