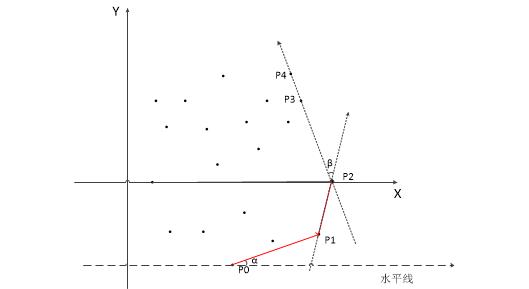
思路:
1.先找到纵坐标最小点p0入栈,遍历剩下的点,找到与水平方向夹角最小的点p1入栈
2.遍历所有点找到与栈顶两个点连线夹角最小的点pn入栈,重复该过程,直道找不出下一个pn
3.栈里的所有点就是凸包上的点
关于怎么找最小角这一步我感觉完全可以替换成每次先把未入栈的一个点入栈,然后遍历剩下所有点,如果某点在栈顶两点连线的右方,用该点顶替栈顶点,每次遍历完所有的点,标记一下栈顶的点,如果栈顶点被标记过,舍弃栈顶元素,剩下的点就是凸包上的所有点。
该式大于零第三个点在前两个点的左方,否则在右方。
以poj1113 Wall为例看一下代码
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <algorithm>
#define inf 0x3f3f3f3f
#define PI acos(-1.0)
#define eps 1e-9
using namespace std;
struct node
{
double x, y;
};
node p[1100];
int s[1100];
int vis[1100];
int top;
double multi(node p1, node p2, node p3)
{
return p1.x * p2.y + p3.x * p1.y + p2.x * p3.y - p3.x * p2.y - p2.x * p1.y - p1.x * p3.y;
}
double dist(node a, node b)
{
return sqrt(pow(a.x-b.x,2) + pow(a.y-b.y,2));
}
void jarvis(int n)
{
node minp;
int i, m;
top = 0;
minp.x = inf;
minp.y = inf;
for(i = 0;i < n;i++)
{
if(p[i].y < minp.y || (p[i].y == minp.y && p[i].x < minp.x))
{
minp = p[i];
m = i;
}
}
s[top++] = m;
vis[m] = 1;
m = top;
int flag = 1;
while(flag)
{
flag = 0;
for(i = 0;i < n;i++)
{
if(top <= m)
{
if(vis[i])
continue;
s[top++] = i;
flag = 1;
continue;
}
if(multi(p[s[top-2]],p[s[top-1]],p[i]) < 0 || (abs(multi(p[s[top-2]],p[s[top-1]],p[i]) == 0) && dist(p[s[top-2]],p[i]) < dist(p[s[top-2]],p[s[top-1]]) && !vis[i]))
{
s[top-1] = i;
flag = 1;
}
}
if(vis[s[top-1]])
break;
vis[s[top-1]] = 1;
m = top;
}
}
int main()
{
int n, i;
double d, sum = 0;
cin>>n>>d;
for(i = 0;i < n;i++)
cin>>p[i].x>>p[i].y;
jarvis(n);
for(i = 0;i < top;i++)
{
sum += dist(p[s[i]],p[s[(i+1)%top]]);
}
printf("%.0lf\n",sum + 2.0 * PI * d);
return 0;
}
























 3952
3952

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








