HMM介绍

Introduction Often we are interested in finding patterns which appear over a space of time. These patterns occur in many areas; the pattern of commands someone uses in instructing a computer, sequences of words in sentences, the sequence of phonemes in spoken words - any area where a sequence of events occurs could produce useful patterns. Consider the simple example of someone trying to deduce the weather from a piece of seaweed - folklore tells us that `soggy' seaweed means wet weather, while `dry' seaweed means sun. If it is in an intermediate state (`damp'), then we cannot be sure. However, the state of the weather is not restricted to the state of the seaweed, so we may say on the basis of an examination that the weather is probably raining or sunny. A second useful clue would be the state of the weather on the preceding day (or, at least, its probable state) - by combining knowledge about what happened yesterday with the observed seaweed state, we might come to a better forecast for today. This is typical of the type of system we will consider in this tutorial. First we will introduce systems which generate probabalistic patterns in time, such as the weather fluctuating between sunny and rainy. We then look at systems where what we wish to predict is not what we observe - the underlying system is hidden. In the above example, the observed sequence would be the seaweed and the hidden system would be the actual weather. We then look at some problems that can be solved once the system has been modeled. For the above example, we may want to know What the weather was for a week given each day's seaweed observation. Given a sequence of seaweed observations, is it winter or summer? Intuitively, if the seaweed has been dry for a while it may be summer, if it has been soggy for a while it might be winter.

Generating Patterns

Deterministic

Non-Deterministic

Summary

---

Section 1 - Page 1

DeterministicPatterns

Consider a set of traffic lights; the sequence of lights isred - red/amber - green - amber - red.The sequence can be pictured as a state machine, where the different states ofthe traffic lights follow each other.

e.g.

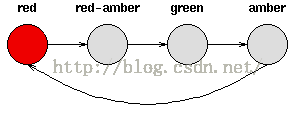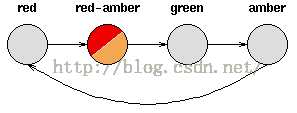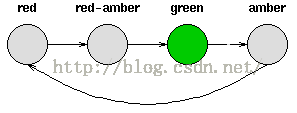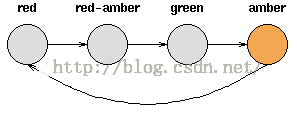
Notice that each state is dependent solely on the previous state,so if the lights are green, an amber light will always follow - that is, thesystem is deterministic. Deterministic systems are relatively easy tounderstand and analyse, once the transitions are fully known.

Patterns generated by a hidden process Limitations of a Markov Process Hidden Markov Models Summary Section 1 - Page 1  1 2   When a Markov process may not be powerful enough In some cases the patterns that we wish to find are not described sufficiently by a Markov process. Returning to the weather example, a hermit may perhaps not have access to direct weather observations, but does have a piece of seaweed. Folklore tells us that the state of the seaweed is probabalistically related to the state of the weather - the weather and seaweed states are closely linked. In this case we have two sets of states, the observable states (the state of the seaweed) and the hidden states (the state of the weather). We wish to devise an algorithm for the hermit to forecast weather from the seaweed and the Markov assumption without actually ever seeing the weather. A more realistic problem is that of recognising speech; the sound that we hear is the product of the vocal chords, size of throat, position of tongue and several other things. Each of these factors interact to produce the sound of a word, and the sounds that a speech recognition system detects are the changing sound generated from the internal physical changes in the person speaking.

Some speech recognition devices work by considering the internal speech production to be a sequence of hidden states, and the resulting sound to be a sequence of observable states generated by the speech process that at best approximates the true (hidden) states. In both examples it is important to note that the number of states in the hidden process and the number of observable states may be different. In a three state weather system (sunny, cloudy, rainy) it may be possible to observe four grades of seaweed dampness (dry, dryish, damp,soggy); pure speech may be described by (say) 80 phonemes, while a physical speech system may generate a number of distinguishable sounds that is either more or less than 80. In such cases the observed sequence of states is probabalistically related to the hidden process. We model such processes using a hidden Markov model where there is an underlying hidden Markov process changing over time, and a set of observable states which are related somehow to the hidden states.

Hidden Markov Models Definition Usages Summary Section 1 - Page 1   Definition of a hidden Markov model A hidden Markov model (HMM) is a triple (,A,B). the vector of the initial state probabilities; the state transition matrix; the confusion matrix; Each probability in the state transition matrix and in the confusion matrix is time independent - that is, the matrices do not change in time as the system evolves. In practice, this is one of the most unrealistic assumptions of Markov models about real processes.

 

 

HMMs - Summary

---

Section 1 - Page 1 
1 2

Summary

Frequently, patterns do not appear in isolation but as part of aseries in time - this progression can sometimes be used to assist in theirrecognition. Assumptions are usually made about the time based process - acommon assumption is that the process's state is dependent only on thepreceding N states - then we have an order N Markov model. The simplest case isN=1.

Various examples exists where the process states (patterns) arenot directly observable, but are indirectly, and probabalistically, observableas another set of patterns - we can then define a hidden Markov model - thesemodels have proved to be of great value in many current areas of research,notably speech recognition.

Such models of real processes pose three problems that areamenable to immediate attack; these are :

• Evaluation : with what probability does a given model generate a given sequence of observations. The forward algorithm solves this problem efficiently.

• Decoding : what sequence of hidden (underlying) states most probably generated a given sequence of observations. The Viterbi algorithm solves this problem efficiently.
• Learning : what model most probably underlies a given sample of observation sequences - that is, what are the parameters of such a model. This problem may be solved by using the forward-backward algorithm.

HMMs have proved to be of great value in analysing real systems; theirusual drawback is the over-simplification associated with the Markov assumption- that a state is dependent only on predecessors, and that this dependence istime independent.

A full expositionon HMMs may be found in:

L R Rabiner and B H Juang, `An introduction to HMMs',iEEE ASSP Magazine, 3, 4-16.

http://www.comp.leeds.ac.uk/roger/HiddenMarkovModels/html_dev/main.html