前言
- 虽然我们在编程语言中可以直接使用+-/,但是对某些要求不能用/的情况下,我们有必要了解一下计算机是怎样完成乘除法的。
- 首先,我们要明确一下计算机所能完成的最基本操作是:+(-)和左移右移。虽然ISA中一般都有MUL类指令,但是这些经过译码之后最终的元操作还是加法和移位指令。
乘法实现
- 我们知道在计算机中只有0和1,于是,就有了二进制计数,比如5 = 101. 抽象的说,任何一个数均可以表示为如下式子:
所以其他数乘以X,就变成了如下式子:
这就是计算机做乘法的原理。因为对于计算机而言,左移一位代表乘以2,右移一位代表除以2。所以,对于a乘以x而言,只是将a左移x为1的位并累加即可。
举例说明:5*3
- 3=0011(不用分解,计算机就是这么存储的)
- 3的第0位1,5左移0位仍为0;
- 3的第一位为1,5左移1位为5*2 = 10
- 然后将其累加,得到最后结果15.
代码如下:
//没有考虑传入数太大,导致溢出的情况。只做简单说明
int getBits(int num){
int numLen = 0;
while(num){
numLen++;
num = num>>1;
}
return numLen;
}
int getIndexBit(int num,int pos){//获取从右到左的第pos位置的值1/0
int index = 1<<pos;
if((num&index)>>pos)
return 1;
else
return 0;
}
int getBit(int num,int pos){//获取从右到左的第pos位置的值1/0
pos = pos-1;
return getIndexBit(num,pos);
}
int multi(int multi1,int multi2){
bool minus = false;
if(multi2<0){
minus = true;
multi2 = -multi2;
}
int length = getBits(multi2);
int index = 0;
int base = multi1;
int sum = 0;
while(index<length){
int val = getBit(multi2,index+1);
if(val)
sum+=(base<<index);
index++;
}
if(minus)
return -sum;
return sum;
}除法实现
除法实现起来要比乘法难一点,因此,让我们首先从人的角度来计算一下除法的实现。
人类计算除法
当我们在计算51/3=17,抛开9*9乘法表。
- 从被除数的最高位5开始,从0-9选一个数,使得5-i*3>=0且使5-(i+1)*3<0。我们选择了1. 余数为2.
- 将余数*10+1=21,继续从0-9中选一个数,使得21-3*i>=0且使5-(i+1)*3<0,我们选择了7.
- 由此,我们找到了答案17。
计算机计算除法
计算机计算除法的过程与人类计算的过程很类似,只是选择范围变成了0或1.
还以51/3为例说明(51:110011;3:11)
- 从第一位开始为1,小于11,结果位置0;余数为1
- 从第二位开始,余数*2+1=11,等于11,结果位置1,余数为0;
- 从第三、四位开始,余数*2+0=0<011,结果位置0,余数为0
- 从第5位开始,余数*2+1=1<11,结果置0,余数为1
- 从第6位开始,余数*2+1=11=11,结果置1,余数为0.
此时将结果位相连,恰好是10001(17)
代码请参见:已通过leetcode-29题测试








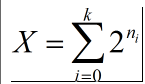
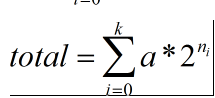
















 2996
2996

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








