2n皇后问题

题目：

思路：

首先在棋盘里把黑皇后放好，然后再放白皇后。
程序需要3个功能：
		1.初始化棋盘
		2.确定皇后的位置
		3.判断皇后能否在这个位置上

三个功能写三个方法：
初始化就在main里面

n:题目要求的皇后个数
b[][]:模拟棋盘
chess:目前是放黑皇后还是白皇后（黑皇后是chess=2，白皇后是chess=3）
判断皇后能否在这个位置上:

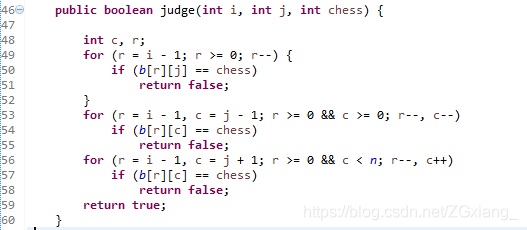
		i,j 为二维数组棋盘的下标；chess是当前是放黑还是白皇后

49~52行：判断列是否有重复，只需要找当前的位置往上找是否有重复就行了。因为我之后的递归条件导致了我不需要判断行是否冲突。

53~55行:判断主对角线是否冲突（即以当前坐标为中心的左上位置）因为本行下面的位置我还没有放皇后，所以只需要考虑本行以上的皇后是否冲突。

56~58行:判断副对角线是否冲突（即以当前坐标为中心的右上位置）

比较复杂难懂的回溯核心来了

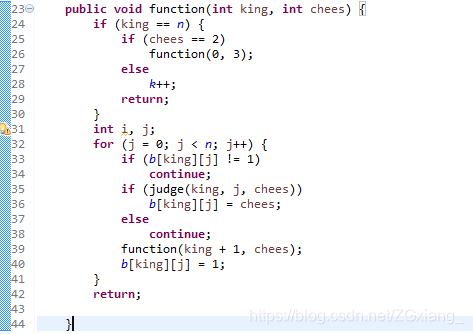
	king:皇后个数，也可以理解为行,因为一行只能放一个皇后.
	k:计数，即有多少种摆法.
	32~41行:找每一行的皇后.
			33行的if是判断当前位置能否放棋子.
			35行就是把当前的位置传过去判断本行该列能否放皇后
			39行递归，本行找好了就递归找下一行的皇后。
			40行如果递归一直找，找到后面几行发现找不到了，说明之前皇后位置找错了
			（不是说皇后有冲突，举个例子 假设第一个皇后放到b[0][0]，
			第二行皇后就可以放b[1][2],b[1][3].....但是可能这个位置不是它真正的位置，
			就把找错的位置置为1，然后接着之前的循环继续找。这就是回溯）
			
	24行:	递归的出口，当king为n说明找完了，24行的if就是判断当前是否找完黑皇后，
			如果找完了，然后重新从第0行开始找白皇后，白皇后找完k++；

完整代码：

在这里插入代码片

import java.util.Scanner;

public class Main {
	static int n, k = 0;
	static int b[][];
	static int chess;

	public static void main(String[] args) {
		Scanner input = new Scanner(System.in);
		int j, i;
		n = input.nextInt();
		b = new int[n][n];
		for (i = 0; i < n; i++)
			for (j = 0; j < n; j++)
				b[i][j] = input.nextInt();
		Main m = new Main();
		m.function(0, 2);
		System.out.println(k);
	}

	public void function(int king, int chees) {
		if (king == n) {
			if (chees == 2)
				function(0, 3);
			else
				k++;
			return;
		}
		int i, j;
		for (j = 0; j < n; j++) {
			if (b[king][j] != 1)
				continue;
			if (judge(king, j, chees))
				b[king][j] = chees;
			else
				continue;
			function(king + 1, chees);
			b[king][j] = 1;
		}
		return;

	}

	public boolean judge(int i, int j, int chess) {

		int c, r;
		for (r = i - 1; r >= 0; r--) {
			if (b[r][j] == chess)
				return false;
		}
		for (r = i - 1, c = j - 1; r >= 0 && c >= 0; r--, c--)
			if (b[r][c] == chess)
				return false;
		for (r = i - 1, c = j + 1; r >= 0 && c < n; r--, c++)
			if (b[r][c] == chess)
				return false;
		return true;
	}
}