BLiTZ（Bayesian Layers in Torch Zoo）blitz-bayesian-pytorch 是一个基于PyTorch的库，它允许用户创建贝叶斯神经网络层,bnn

BLiTZ（Bayesian Layers in Torch Zoo）是一个基于PyTorch的库，它允许用户创建贝叶斯神经网络层。这个库的设计目标是简化在神经网络中引入不确定性的过程，使得用户可以轻松地收集模型的复杂性成本，而不会干扰层与层之间的交互。BLiTZ提供了核心的权重采样器类，用户可以通过这些类扩展并改进库，以便在更广泛的层中引入不确定性。

A simple and extensible library to create Bayesian Neural Network Layers on PyTorch without trouble and with full integration with nn.Module and nn.Sequential.

copied from cf-staging / blitz-bayesian-pytorch

github.com/piEsposito/blitz-bayesian-deep-learning

•  License: GPL-3.0-only
•  Home: GitHub - piEsposito/blitz-bayesian-deep-learning: A simple and extensible library to create Bayesian Neural Network layers on PyTorch.
•  3905 total downloads
•  Last upload: 2 years and 4 months ago

blitz-bayesian-pytorch · PyPI

 pypi.org/project/blitz-bayesian-pytorch/，

注意包名 是blitz-bayesian-pytorch/ 不是 blitz

安装BLiTZ可以通过pip命令：
```
pip install blitz-bayesian-pytorch
```
或者通过conda：
```
conda install -c conda-forge blitz-bayesian-pytorch
```
也可以通过git克隆并本地安装：
```
conda create -n blitz python=3.6
conda activate blitz
git clone https://github.com/piEsposito/blitz-bayesian-deep-learning.git
cd blitz-bayesian-deep-learning
pip install .
```

Successfully installed blitz-bayesian-pytorch-0.2.8
 

BLiTZ提供了贝叶斯层、权重和先验分布采样器以及与PyTorch集成的实用工具。它还可以用于回归问题，以收集数据点的置信区间，而不仅仅是一个点预测值。例如，可以创建一个贝叶斯神经网络回归器，用于预测波士顿房价数据集，尝试为房价预测创建75%的置信区间。

使用BLiTZ的训练循环与传统的PyTorch训练循环不同之处在于，它通过`sample_elbo`方法对损失进行采样。以下是一个简单的训练循环示例：
```python
import torch
import torch.nn as nn
import torch.optim as optim
from blitz.modules import BayesianLinear
from blitz.utils import variational_estimator

@variational_estimator
class BayesianNetwork(nn.Module):
    def __init__(self):
        super().__init__()
        self.layer1 = BayesianLinear(1, 10)
        self.layer2 = BayesianLinear(10, 1)

    def forward(self, x):
        x = torch.relu(self.layer1(x))
        x = self.layer2(x)
        return x

model = BayesianNetwork()
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

for epoch in range(100):
    optimizer.zero_grad()
    x = torch.randn(32, 1)
    y_pred = model(x)
    loss = model.sample_elbo(inputs=x, labels=y_pred, criterion=criterion, sample_nbr=3)
    loss.backward()
    optimizer.step()
```

BLiTZ可以应用于金融风险评估、医疗诊断和自动驾驶等领域，以引入不确定性并提高模型的鲁棒性和可靠性。使用BLiTZ时，应注意超参数调整、模型评估和复杂性成本收集等最佳实践。

更多详细信息和文档，可以参考BLiTZ的官方文档和GitHub仓库。

==========================================================

Pypi.ory 里面的介绍

BLiTZ是一个简单且可扩展的库，用于创建贝叶斯神经网络层(基于神经网络论文中的权重不确定性)上PyTorch。通过使用BLiTZ层和utils，您可以以一种简单的方式添加不确定性并收集模型的复杂性成本，而不会影响层之间的交互，就像您使用标准PyTorch一样。

通过使用我们的核心权重采样器类，您可以扩展和改进这个库，以将不确定性添加到更大范围的层中，就像您将以一种与PyTorch良好集成的方式那样。也欢迎拉请求。

我们的目标是让人们能够通过关注他们的想法而不是硬编码部分来应用贝叶斯深度学习。

索引

• 安装
• 证明文件
• 回归的一个简单例子
  • 导入必要的模块
  • 加载和缩放数据
  • 创建我们的变分回归类
  • 定义置信区间评估函数
  • 创建回归变量并加载数据
  • 我们的主要培训和评估循环
• 简而言之，贝叶斯深度学习
  • 首先，确定性NN层线性变换
  • 贝叶斯层的用途
  • 贝叶斯层上的加权抽样
  • 优化我们的可训练重量是可能的
  • 这也是事实，有复杂的成本函数微分沿其变量
  • 为了获得第n个样本的整个成本函数
  • 一些笔记和总结
• 引用
• 参考

安装

要安装BLiTZ，您可以使用pip命令:

pip install blitz-bayesian-pytorch

或者，通过conda:

conda install -c conda-forge blitz-bayesian-pytorch

您也可以git-clone它并在本地pip-install它:

conda create -n blitz python=3.6
conda activate blitz
git clone https://github.com/piEsposito/blitz-bayesian-deep-learning.git
cd blitz-bayesian-deep-learning
pip install .

证明文件

我们的层、重量(和先前分布)取样器和工具的文件:

• 贝叶斯层
• 重量和先验分布取样器
• Utils(便于与PyTorch集成)
• 损耗

回归的一个简单例子

(自己跑一跑就能看出来这个例子在您的机器上)。

我们现在将看到贝叶斯深度学习如何用于回归，以便在我们的数据点上收集置信区间，而不是一个潜在的连续值预测。为你的预测收集一个置信区间可能比低误差估计更有用。

我坚持我的论点，事实上，有了好/高概率置信区间，在某些情况下，你可以做出比非常接近的估计更可靠的决定:例如，如果你试图从一项交易操作中获利，有了好的置信区间可以让你知道，至少，操作将进行的价值将低于(或高于)某个确定的x。

知道一个值是否肯定(或很有可能)在一个确定的区间上，比非常接近的估计更能帮助人们做出明智的决定，如果低于或高于某个极限值，可能会导致交易损失。重点是，有时候，知道是否会有利润，可能比衡量利润更有用。

为了证明这一点，我们将为Boston-house-data toy数据集创建一个贝叶斯神经网络回归器，试图为我们试图预测其价格的房屋创建置信区间(CI)。我们将执行一些缩放，CI大约为75%。有趣的是，约90%的预测顺式低于上限或高于下限。

导入必要的模块

尽管从已知的模块，我们将从闪电战variational_estimatordecorator，它帮助我们处理模块上的Bayesian线性层，保持它与Torch的其余部分完全集成，当然，BayesianLinear，这是我们的层的特点是重量不确定性。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import numpy as np

from blitz.modules import BayesianLinear
from blitz.utils import variational_estimator

from sklearn.datasets import load_boston
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split

加载和缩放数据

这并不是什么新鲜事，我们正在导入和标准化数据来帮助训练。

X, y = load_boston(return_X_y=True)
X = StandardScaler().fit_transform(X)
y = StandardScaler().fit_transform(np.expand_dims(y, -1))

X_train, X_test, y_train, y_test = train_test_split(X,
                                                    y,
                                                    test_size=.25,
                                                    random_state=42)


X_train, y_train = torch.tensor(X_train).float(), torch.tensor(y_train).float()
X_test, y_test = torch.tensor(X_test).float(), torch.tensor(y_test).float()

创建我们的变分回归类

我们可以用从nn中调用来创建我们的类。模块，就像我们对任何火炬网络所做的那样。我们的decorator介绍了处理贝叶斯特征的方法，如计算贝叶斯层的复杂性成本和进行许多前馈(对每个层采样不同的权重)以采样我们的损失。

@variational_estimator
class BayesianRegressor(nn.Module):
    def __init__(self, input_dim, output_dim):
        super().__init__()
        #self.linear = nn.Linear(input_dim, output_dim)
        self.blinear1 = BayesianLinear(input_dim, 512)
        self.blinear2 = BayesianLinear(512, output_dim)
        
    def forward(self, x):
        x_ = self.blinear1(x)
        x_ = F.relu(x_)
        return self.blinear2(x_)

定义置信区间评估函数

该函数确实为我们试图对标签值进行采样的批次上的每个预测创建了一个置信区间。然后，我们可以通过寻找有多少预测分布实际上包含了数据点的正确标签来衡量我们预测的准确性。

def evaluate_regression(regressor,
                        X,
                        y,
                        samples = 100,
                        std_multiplier = 2):
    preds = [regressor(X) for i in range(samples)]
    preds = torch.stack(preds)
    means = preds.mean(axis=0)
    stds = preds.std(axis=0)
    ci_upper = means + (std_multiplier * stds)
    ci_lower = means - (std_multiplier * stds)
    ic_acc = (ci_lower <= y) * (ci_upper >= y)
    ic_acc = ic_acc.float().mean()
    return ic_acc, (ci_upper >= y).float().mean(), (ci_lower <= y).float().mean()

创建回归变量并加载数据

注意这里我们创建了我们的BayesianRegressor就像我们对待其他神经网络一样。

regressor = BayesianRegressor(13, 1)
optimizer = optim.Adam(regressor.parameters(), lr=0.01)
criterion = torch.nn.MSELoss()

ds_train = torch.utils.data.TensorDataset(X_train, y_train)
dataloader_train = torch.utils.data.DataLoader(ds_train, batch_size=16, shuffle=True)

ds_test = torch.utils.data.TensorDataset(X_test, y_test)
dataloader_test = torch.utils.data.DataLoader(ds_test, batch_size=16, shuffle=True)

我们的主要培训和评估循环

我们做了一个训练循环，它与普通torch训练的唯一不同之处是它的sample_elbo方法对其损耗进行了采样。所有其他的事情都可以正常完成，因为我们使用BLiTZ的目的是让你轻松地用不同的贝叶斯神经网络迭代数据。

这是我们非常简单的训练循环:

iteration = 0
for epoch in range(100):
    for i, (datapoints, labels) in enumerate(dataloader_train):
        optimizer.zero_grad()
        
        loss = regressor.sample_elbo(inputs=datapoints,
                           labels=labels,
                           criterion=criterion,
                           sample_nbr=3)
        loss.backward()
        optimizer.step()
        
        iteration += 1
        if iteration%100==0:
            ic_acc, under_ci_upper, over_ci_lower = evaluate_regression(regressor,
                                                                        X_test,
                                                                        y_test,
                                                                        samples=25,
                                                                        std_multiplier=3)
            
            print("CI acc: {:.2f}, CI upper acc: {:.2f}, CI lower acc: {:.2f}".format(ic_acc, under_ci_upper, over_ci_lower))
            print("Loss: {:.4f}".format(loss))

简而言之，贝叶斯深度学习

快速解释不确定性是如何在贝叶斯神经网络中引入的，以及我们如何对其损失建模，以便客观地提高其预测的可信度，并在不丢失的情况下减少方差。

首先，确定性NN层线性变换

正如我们所知，在确定性(非贝叶斯)神经网络层上，可训练参数直接对应于前一个(或输入，如果是这种情况)的线性变换上使用的权重。它对应于以下等式:

(Z对应于层I的激活输出)

贝叶斯层的用途

贝叶斯层试图通过从由每个前馈操作的可训练变量参数化的分布中采样来引入其权重的不确定性。

这使得我们不仅可以优化模型的性能指标，还可以收集特定数据点上网络预测的不确定性(通过多次采样并测量离差)，并有目的地尽可能多地减少预测上网络的方差，从而可以知道如果我们尝试根据特定数据点的函数对标签进行建模，我们还有多少不确定性。

贝叶斯层上的加权抽样

为此，在每个前馈操作中，我们用以下等式对线性变换的参数进行采样(其中ρ参数化标准偏差和μ参数化样本线性变换参数的平均值) :

对于重量:

其中采样的W对应于在第n个样本的第I层的线性变换中使用的权重。

对于偏见:

其中采样的b对应于在第n个样本的第I层的线性变换中使用的偏差。

优化我们的可训练重量是可能的

即使我们的权重和偏差有一个随机乘数，也可以通过给定一些采样权重的可微分函数和可训练参数(在我们的例子中是损失)，对两者的导数求和来优化权重和偏差:

1. 让

   

2. 让

   

3. 让

   

4. 让

   

   相对于它的变量可微

因此:

1. 

和

1. 

这也是事实，有复杂的成本函数微分沿其变量

众所周知，交叉熵损失(和MSE)是可微的。因此，如果我们证明存在可微分的复杂性成本函数，我们可以将它留给我们的框架，在优化步骤中求导数并计算梯度。

在前馈操作上，通过每个贝叶斯层计算复杂性成本(具有预定义的层-更简单的先验分布及其经验分布)。每一层的复杂度成本之和加起来就是损失。

如中所提议的神经网络论文中的权重不确定性，我们可以通过获取库尔贝克-莱布勒散度从它到一个简单得多的分布，并且通过作一些近似，我们将可以相对于它的变量来区分这个函数(这个分布):

1. 让

   

   是手动设置的低熵分布pdf，其将被假设为权重的“先验”分布

2. 让

   

   在给定参数的情况下，是样本权重的后验经验分布pdf。

因此，对于W采样矩阵上的每个标量:

1. 

假设n非常大，我们可以近似得出:

1. 

因此:

1. 

由于Q分布的期望(均值)最终只是通过缩放值，我们可以将其从等式中去掉(因为没有框架跟踪)。第n个样本的复杂性成本为:

1. 

它相对于所有的参数都是可微的。

要获得第n个样本的整个成本函数:

1. 假设一个性能(适合数据)函数是:

   

因此，第n个权重样本的总成本函数为:

1. 

我们可以通过蒙特卡洛采样(前馈网络X次，取全损耗的平均值)来估计真实的全成本函数，然后使用我们的估计值反向传播。它适用于每个反向投影的少量实验，甚至适用于单一实验。

一些笔记和总结

我们来到了贝叶斯深度学习的核心教程。通过了解这里正在做的事情，您可以如您所愿地实现您的bnn模型。

也许你可以通过对每个样本做一个优化步骤来进行优化，或者使用这种蒙特卡罗方法来收集一些损失，取其平均值，然后进行优化。该你了。

仅供参考:我们的贝叶斯层和实用工具有助于计算每个前馈操作的复杂性成本，所以不要太在意。

参考资料:

• 查尔斯·布伦德尔、朱利安·科尔内比斯、科雷·卡武克库奥卢和金奎大·威斯特拉。神经网络中的权重不确定性。arXiv预印本arXiv:1505.05424，2015。

-=================================================================

下面的实例  ，来源  zhuanlan.zhihu.com/p/137185084 

 https://zhuanlan.zhihu.com/p/137185084

Pytorch贝叶斯深度学习库BLiTZ实现LSTM模型预测时序数据并绘制置信区间

文将主要讲述如何使用BLiTZ（PyTorch贝叶斯深度学习库）来建立贝叶斯LSTM模型，以及如何在其上使用序列数据进行训练与推理。

在本文中，我们将解释贝叶斯长期短期记忆模型（LSTM）是如何工作的，然后通过一个Kaggle数据集进行股票置信区间的预测。

贝叶斯LSTM层

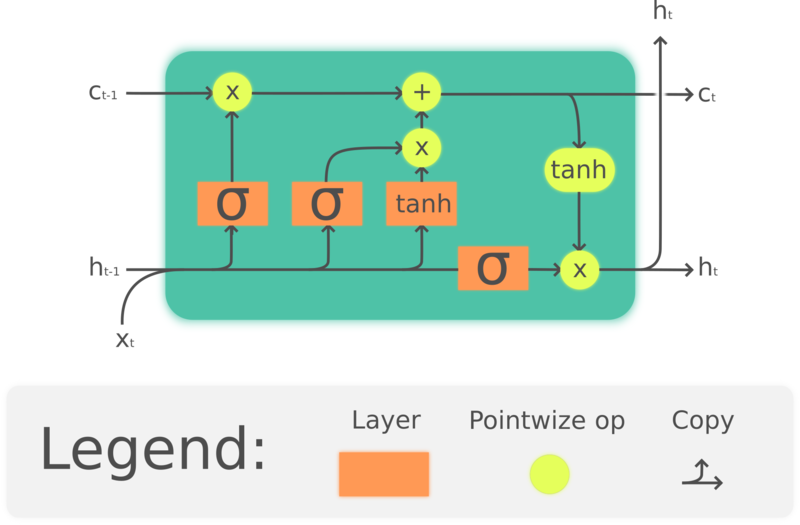
众所周知，LSTM结构旨在解决使用标准的循环神经网络（RNN）处理长序列数据时发生的信息消失问题。

在数学上，LSTM结构的描述如下：

我们知道，贝叶斯神经网络的核心思想是，相比设定一个确定的权重，我们可以通过一个概率密度分布来对权重进行采样，然后优化分布参数。

利用这一点，就有可能衡量我们所做的预测的置信度和不确定性，这些数据与预测本身一样，都是非常有用的数据。

从数学上讲，我们只需要在上面的方程中增加一些额外的步骤，也即权值和偏置的采样，这发生在前向传播之前。

这表示在第i次在模型第N层上权重的采样。

这表示在第i次在模型第N层上偏置的采样。

当然，我们的可训练参数是和，用来表示不同的权重分布。 BLiTZ具有内置的BayesianLSTM层，可以为您完成所有这些艰苦的工作，因此您只需要关注您的网络结构设计与网络的训练/测试。

现在我们看一个例子。

第一步，先导入库

除了导入深度学习中最常用的库外，我们还需要从blitz.modules中导入BayesianLSTM，并从blitz.utils导入variational_estimator，后者是一个用于变量训练与复杂度计算的装饰器。

我们还要导入collections.deque来执行时间序列数据的预处理。

import pandas as pd
import numpy as np

import torch
import torch.nn as nn
import torch.optim as optim
import torch.nn.functional as F

from blitz.modules import BayesianLSTM
from blitz.utils import variational_estimator

from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

import matplotlib.pyplot as plt
%matplotlib inline

from collections import deque

数据预处理

现在，我们将创建并预处理数据集以将其输入到网络。 我们将从Kaggle数据集中导入Amazon股票定价，获取其“收盘价”数据并将其标准化。

我们的数据集将由标准化股票价格的时间戳组成，并且具有一个形如(batch_size，sequence_length，observation_length)的shape。

下面我们导入数据并对其预处理：

#importing the dataset
amazon="data/AMZN_2006-01-01_to_2018-01-01.csv"
ibm="data/IBM_2006-01-01_to_2018-01-01.csv"
df = pd.read_csv(ibm)

#scaling and selecting data
close_prices = df["Close"]
scaler = StandardScaler()

close_prices_arr = np.array(close_prices).reshape(-1, 1)
close_prices = scaler.fit_transform(close_prices_arr)

close_prices_unscaled = df["Close"]

我们还必须创建一个函数来按照时间戳转换我们的股价历史记录。 为此，我们将使用最大长度等于我们正在使用的时间戳大小的双端队列，我们将每个数据点添加到双端队列，然后将其副本附加到主时间戳列表：

def create_timestamps_ds(series,
timestep_size=window_size):
time_stamps = []
labels = []
aux_deque = deque(maxlen=timestep_size)

#starting the timestep deque
for i in range(timestep_size):
aux_deque.append(0)

#feed the timestamps list
for i in range(len(series)-1):
aux_deque.append(series[i])
time_stamps.append(list(aux_deque))

#feed the labels lsit
for i in range(len(series)-1):
labels.append(series[i + 1])

assert len(time_stamps) == len(labels), "Something went wrong"

#torch-tensoring it
features = torch.tensor(time_stamps[timestep_size:]).float()
labels = torch.tensor(labels[timestep_size:]).float()

return features, labels

创建神经网络类

我们的网络类接收variantal_estimator装饰器，该装饰器可简化对贝叶斯神经网络损失的采样。我们的网络具有一个贝叶斯LSTM层，参数设置为in_features = 1以及out_features = 10，后跟一个nn.Linear(10, 1)，该层输出股票的标准化价格。

@variational_estimator
class NN(nn.Module):
def __init__(self):
super(NN, self).__init__()
self.lstm_1 = BayesianLSTM(1, 10)
self.linear = nn.Linear(10, 1)

def forward(self, x):
x_, _ = self.lstm_1(x)

#gathering only the latent end-of-sequence for the linear layer
x_ = x_[:, -1, :]
x_ = self.linear(x_)
return x_

如您所见，该网络可以正常工作，唯一的不同点是BayesianLSTM层和variantal_estimator装饰器，但其行为与一般的Torch对象相同。

完成后，我们可以创建我们的神经网络对象，分割数据集并进入训练循环：

创建对象

我们现在可以创建损失函数、神经网络、优化器和dataloader。请注意，我们不是随机分割数据集，因为我们将使用最后一批时间戳来计算模型。由于我们的数据集很小，我们不会对训练集创建dataloader。

Xs, ys = create_timestamps_ds(close_prices)
X_train, X_test, y_train, y_test = train_test_split(Xs,
ys,
test_size=.25,
random_state=42,
shuffle=False)



ds = torch.utils.data.TensorDataset(X_train, y_train)
dataloader_train = torch.utils.data.DataLoader(ds, batch_size=8, shuffle=True)

net = NN()

criterion = nn.MSELoss()
optimizer = optim.Adam(net.parameters(), lr=0.001)

我们将使用MSE损失函数和学习率为0.001的Adam优化器

训练循环

对于训练循环，我们将使用添加了variational_estimator的sample_elbo方法。 它对X个样本的损失进行平均，并帮助我们轻松地用蒙特卡洛估计来计算损失。

为了使网络正常工作，网络forward方法的输出必须与传入损失函数对象的标签的形状一致。

iteration = 0
for epoch in range(10):
for i, (datapoints, labels) in enumerate(dataloader_train):
optimizer.zero_grad()

loss = net.sample_elbo(inputs=datapoints,
labels=labels,
criterion=criterion,
sample_nbr=3)
loss.backward()
optimizer.step()

iteration += 1
if iteration%250==0:
preds_test = net(X_test)[:,0].unsqueeze(1)
loss_test = criterion(preds_test, y_test)
print("Iteration: {} Val-loss: {:.4f}".format(str(iteration), loss_test))

评估模型并计算置信区间

我们将首先创建一个具有要绘制的真实数据的dataframe：

original = close_prices_unscaled[1:][window_size:]

df_pred = pd.DataFrame(original)
df_pred["Date"] = df.Date
df["Date"] = pd.to_datetime(df_pred["Date"])
df_pred = df_pred.reset_index()

要预测置信区间，我们必须创建一个函数来预测同一数据X次，然后收集其均值和标准差。 同时，在查询真实数据之前，我们必须设置将尝试预测的窗口大小。

让我们看一下预测函数的代码：

def pred_stock_future(X_test,
future_length,
sample_nbr=10):

#sorry for that, window_size is a global variable, and so are X_train and Xs
global window_size
global X_train
global Xs
global scaler

#creating auxiliar variables for future prediction
preds_test = []
test_begin = X_test[0:1, :, :]
test_deque = deque(test_begin[0,:,0].tolist(), maxlen=window_size)

idx_pred = np.arange(len(X_train), len(Xs))

#predict it and append to list
for i in range(len(X_test)):
#print(i)
as_net_input = torch.tensor(test_deque).unsqueeze(0).unsqueeze(2)
pred = [net(as_net_input).cpu().item() for i in range(sample_nbr)]


test_deque.append(torch.tensor(pred).mean().cpu().item())
preds_test.append(pred)

if i % future_length == 0:
#our inptus become the i index of our X_test
#That tweak just helps us with shape issues
test_begin = X_test[i:i+1, :, :]
test_deque = deque(test_begin[0,:,0].tolist(), maxlen=window_size)

#preds_test = np.array(preds_test).reshape(-1, 1)
#preds_test_unscaled = scaler.inverse_transform(preds_test)

return idx_pred, preds_test

我们要将置信区间保存下来，确定我们置信区间的宽度。

def get_confidence_intervals(preds_test, ci_multiplier):
global scaler

preds_test = torch.tensor(preds_test)

pred_mean = preds_test.mean(1)
pred_std = preds_test.std(1).detach().cpu().numpy()

pred_std = torch.tensor((pred_std))

upper_bound = pred_mean + (pred_std * ci_multiplier)
lower_bound = pred_mean - (pred_std * ci_multiplier)
#gather unscaled confidence intervals

pred_mean_final = pred_mean.unsqueeze(1).detach().cpu().numpy()
pred_mean_unscaled = scaler.inverse_transform(pred_mean_final)

upper_bound_unscaled = upper_bound.unsqueeze(1).detach().cpu().numpy()
upper_bound_unscaled = scaler.inverse_transform(upper_bound_unscaled)

lower_bound_unscaled = lower_bound.unsqueeze(1).detach().cpu().numpy()
lower_bound_unscaled = scaler.inverse_transform(lower_bound_unscaled)

return pred_mean_unscaled, upper_bound_unscaled, lower_bound_unscaled

由于我们使用的样本数量很少，因此用一个很高的标准差对其进行了补偿。 我们的网络将尝试预测7天，然后将参考数据：

future_length=7
sample_nbr=4
ci_multiplier=10
idx_pred, preds_test = pred_stock_future(X_test, future_length, sample_nbr)
pred_mean_unscaled, upper_bound_unscaled, lower_bound_unscaled = get_confidence_intervals(preds_test,
ci_multiplier)

我们可以通过查看实际值是否低于上限并高于下限来检查置信区间。 设置好参数后，您应该拥有95％的置信区间，如下所示：

y = np.array(df.Close[-750:]).reshape(-1, 1)
under_upper = upper_bound_unscaled > y
over_lower = lower_bound_unscaled < y
total = (under_upper == over_lower)

print("{} our predictions are in our confidence interval".format(np.mean(total)))

检查输出图形

现在，我们将把预测结果绘制为可视化图形来检查我们的网络是否运行的很顺利，我们将在置信区间内绘制真实值与预测值。

params = {"ytick.color" : "w",
"xtick.color" : "w",
"axes.labelcolor" : "w",
"axes.edgecolor" : "w"}
plt.rcParams.update(params)

plt.title("IBM Stock prices", color="white")

plt.plot(df_pred.index,
df_pred.Close,
color='black',
label="Real")

plt.plot(idx_pred,
pred_mean_unscaled,
label="Prediction for {} days, than consult".format(future_length),
color="red")

plt.fill_between(x=idx_pred,
y1=upper_bound_unscaled[:,0],
y2=lower_bound_unscaled[:,0],
facecolor='green',
label="Confidence interval",
alpha=0.5)

plt.legend()

最后，我们放大一下着重看看预测部分。

params = {"ytick.color" : "w",
"xtick.color" : "w",
"axes.labelcolor" : "w",
"axes.edgecolor" : "w"}
plt.rcParams.update(params)

plt.title("IBM Stock prices", color="white")


plt.fill_between(x=idx_pred,
y1=upper_bound_unscaled[:,0],
y2=lower_bound_unscaled[:,0],
facecolor='green',
label="Confidence interval",
alpha=0.75)

plt.plot(idx_pred,
df_pred.Close[-len(pred_mean_unscaled):],
label="Real",
alpha=1,
color='black',
linewidth=0.5)

plt.plot(idx_pred,
pred_mean_unscaled,
label="Prediction for {} days, than consult".format(future_length),
color="red",
alpha=0.5)

plt.legend()