ACM常用算法

1）递推求解：首先，确认：能否容易的得到简单情况的解；然后，假设：规模为N-1的情况已经得到解决；最后，重点分析：当规模扩大到N时，如何枚举出所有的情况，并且要确保对于每一种子情况都能用已经得到的数据解决。

例题1 在一个平面上有一个圆和n条直线，这些直线中每一条在圆内同其他直线相交，假设没有3条直线相交于一点，试问这些直线将圆分成多少区域。

分析 F(1)=2;F(n) = F(n-1)+n;化简后为F(n) = n(n+1)/2 +1;

例题2 平面上有n条折线，问这些折线最多能将平面分割成多少块?

分析 把折线当作两天直线相交然后再减去交集延伸部分。F = 2n ( 2n + 1 ) / 2 + 1 - 2n; 

 

2）贪心算法：在对问题求解时，总是作出在当前看来是最好的选择。也就是说，不从整体上加以考虑，它所作出的仅仅是在某种意义上的局部最优解（是否是全局最优，需要证明）。贪心算法的基本步骤包括1、从问题的某个初始解出发。2、采用循环语句，当可以向求解目标前进一步时，就根据局部最优策略，得到一个部分解，缩小问题的范围或规模。3、将所有部分解综合起来，得到问题的最终解。

例题1 已知N个事件的发生时刻和结束时刻（见下表，表中事件已按结束时刻升序排序）。一些在时间上没有重叠的事件，可以构成一个事件序列，如事件
{2，8，10}。事件序列包含的事件数目，称为该事件序列的长度。请编程找出一个最长的事件序列。

分析 不妨用Begin[i]和End[i]表示事件i的开始时刻和结束时刻。则原题的要求就是找一个最长的序列a1<a2<…<an，满足：Begin[a1]<End[a1]<=…<= Begin[an]<End[an]；可以证明，如果在可能的事件a1<a2<…<an中选取在时间上不重叠的最长序列，那么一定存在一个包含a1（结束最早）的最长序列。

 

 

3）动态规划：如果各个子问题不是独立的，不同的子问题的个数只是多项式量级，如果我们能够保存已经解决的子问题的答案，而在需要的时候再找出已求得的答案，这样就可以避免大量的重复计算。由此而来的基本思路是——用一个表记录所有已解决的子问题的答案，不管该问题以后是否被用到，只要它被计算过，就将其结果填入表中。

例题1 有形如下图所示的数塔，从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的值最大。

 

分析 从顶点出发时到底向左走还是向右走应取决于是从左走能取到最大值还是从右走能取到最大值，只要左右两道路径上的最大值求出来了才能作出决策。同样，下一层的走向又要取决于再下一层上的最大值是否已经求出才能决策。这样一层一层推下去，直到倒数第二层时就非常明了。如数字2，只要选择它下面较大值的结点19前进就可以了。所以实际求解时，可从底层开始，层层递进，最后得到最大值。

例题2 最长公共子序列问题：
Sample Input

abcfbc abfcab

programming contest

abcd mnp
Sample Output

4

  2 

0

分析

由于f(i,j)只和f(i-1,j-1), f(i-1,j)和f(i,j-1)有关, 而在计算f(i,j)时, 只要选择一个合适的顺序, 就可以保证这三项都已经计算出来了, 这样就可以计算出f(i,j). 这样一直推到f(len(a),len(b))就得到所要求的解了。

4）母函数：

x2项的系数a1a2+a1a3+...+an-1an中所有的项包括n个元素a1，a2， …an中取两个组合的全体；同理：x3项系数包含了从n个元素a1，a2， …an中取3个元素组合的全体；以此类推。

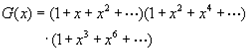
对于序列a0，a1，a2，…构造一函数：

称函数G(x)是序列a0，a1，a2，…的母函数。

例题1 若有1克、2克、3克、4克的砝码各一 枚，能称出哪几种重量？各有几种可能方案？

分析 如何解决这个问题呢？考虑构造母函数。如果用x的指数表示称出的重量，则：1个1克的砝码可以用函数1+x表示，1个2克的砝码可以用函数1+x2表示，1个3克的砝码可以用函数1+x3表示，1个4克的砝码可以用函数1+x4表示。
(1+x)(1+x2)(1+x3)(1+x4)
=(1+x+x2+x3)(1+x3+x4+x7)
=1+x+x2+2x3+2x4+2x5+2x6+2x7+x8+x9+x10
从上面的函数知道：可称出从1克到10克，系数便是方案数。例如右端有2x5 项，即称出5克的方案有2：5=3+2=4+1；同样，6=1+2+3=4+2；10=1+2+3+4。故称出6克的方案有2，称出10克的方案有1。

例题2 求用1分、2分、3分的邮票贴出不同数值的方案数?

分析 因邮票允许重复，故母函数为：

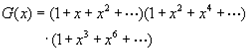
以展开后的x4为例，其系数为4，即4拆分成1、2、3之和的拆分数为4；即 ：4=1+1+1+1=1+1+2=1+3=2+2