实验三 两种群竞争模型的稳定性分析

实验题目 数值模拟分析两种群的稳定性
实验目的 会编程求常微分方程组的数值解，辅助分析竞争模型的稳定性
实验学时 2
实验软件 Matlab
原理方法 M文件的编写，常微分方程数值解的求解，不同参数、初值情况下解的对比分析。
实验内容 数值解辅助分析常微分方程组。
实验步骤 1. 建立两种群竞争模型

function model()
% 设置初始值    
    X1_0 = 1;   
    X2_0 = 2;  
    y0 = [X1_0, X2_0]; 
    % 时间范围
    tspan = [0, 50]; 
    % 解微分方程
    [x, y] = ode45(@ode, tspan, y0);  
    
    plot(x, y),grid;  % 绘制曲线
    legend('x1(t)', 'x2(t)');  % 图例
    xlabel('时间');  % X轴标签
    
    ylabel('数量');  % Y轴标签
    
    title('竞争模型');  % 图标题
    saveas(gcf, '竞争模型.png');
    pause;
    plot(y(:,1), y(:,2), 'LineWidth', 2), grid  % 作相轨线
    
    title('相轨线');  % 图标题
    saveas(gcf, '相轨线.png');
end

function dydt = ode(x, y)
    % 获取状态变量 
    x1 = y(1);  
    x2 = y(2); 
    % 设置参数值
    r1 = 1;  
    r2 = 1;  
    N1 = 100;  
    N2 = 100; 
    xita1 = 0.8;  
    xita2 = 0.7; 
    % 建立微分方程
    X1t = r1 * x1 * (1 - x1 / N1 - xita1 * x2 / N2);  
    X2t = r2 * x2 * (1 - xita2 * x1 / N1 - x2 / N2);  
    dydt = [X1t; X2t];  % 返回微分方程组结果
end

2.计算不同参数情况下的方程数值解并作图，对比分析平衡点的稳定条件。
r1 = 1; r2 = 1;
N1 = 100; N2 = 100;
xita1 = 0.5; xita2 = 2;

最后数值稳定在x1=100,x2=0上， 即物种甲达到最大值， 物种乙灭绝。

r1 = 0.3; r2 = 0.3;
N1 = 100; N2 = 100;
xita1 = 0.5; xita2 = 2;

仍然为甲达到数量极限而乙灭绝，不同的是，由于自然增长率变小，变化速度减缓了。

r1=1;r2=1;
N1=10000;N2=100 ;
xita1 = 0.5; xita2 = 2;

由于一开始甲物种的数量相对较少，所以乙物种得以快速增长，数量一度达到90以上，但最终仍然灭绝。因此物种容量的改变并不能影响最终谁会灭绝。

X1_0=10;X2_0=100;
r1 = 1; r2 = 1;
N1 = 100; N2 = 100;
xita1 = 0.5; xita2 = 2;


乙物种的初始数量大使其灭绝时间稍稍延后，但它灭绝的趋势不变。

r1 = 1; r2 = 1;
N1 = 100; N2 = 100;
xita1 = 1.5; xita2 = 0.7;


最后甲物种灭绝，乙物种存活并达到数量极限

r1 = 1; r2 = 1;
N1 = 100; N2 = 100;
xita1 = 0.8; xita2 = 0.7;


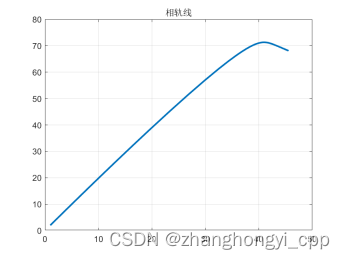
两物种共存，最终数量稳定。

3总结平衡点稳定性条件
从2图中可知，无论怎样改变r1、r2、N1、N2，都改变不了最后甲物种存活并达到数量最大且乙物种灭绝的结果。而改变xita后，甲乙物种的关系出现了明显的改变，xita1 = 0.5;、xita2 = 2，甲物种存活，乙物种灭绝；xita1 = 0.5;、xita2 = 2;，甲物种灭绝，乙物种存活；xita1 = 0.8; xita2 = 0.7;两物种共存。所以，
r1、r2改变只会改变达到平衡点的时间，物种容量和初始数量的改变也只会改变达到平衡点的时间，而xita会改变到达平衡点之后的物种间关系。