灰度图像的sobel边缘检测算法

之前上一篇文章写了如何将图片进行灰度化处理，这篇文章参考CB的文章简单的介绍一下如何进行sobel边缘化处理。

边缘 ： 周围像素灰度急剧变化的那些像素的集合，它是图像最基本的特征

公式 ： 

　　　　

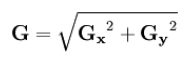
这里Gx和Gy分别代表横向及纵向边缘检测的图像灰度值，该点灰度值大小为G，式子里A代表经过灰度

处理的原始图像，最终计算出来的结果和设定的阈值进行比较如果大于阈值显示一个颜色，否则就显示其他

颜色即可。

 

 

 

采用流水线的方法：

　　1、移位，A是一个3X3的矩阵，需要不断的刷新，我用的是9个寄存器，每一个时钟就刷新一次。

　　2、计算Gx 和Gy，矩阵相乘展开以后就是几个数据相乘，因为矩阵因子里面有负数，所以需要

　　　　　　　　　　比较大小，把正值给保留下来。

　　3、求平方和

　　4、利用altera自带的IP核，实现开根号处理。

　　5、跟阈值进行比较

/*-----------------------------------------------------------------------

Date                :        2017-XX-XX
Description            :        Design for .

-----------------------------------------------------------------------*/

module sobel
(
    //global clock
    input                    clk,            //system clock
    input                    rst_n,             //sync reset
    
    //gray interface
    input            [7:0]    gray,
    
    //sobel    interface
    output            [10:0]    sobel_data
    
); 


//--------------------------------
//Funtion :  变量声明

reg            [7:0]        matrix_p11 , matrix_p12 , matrix_p13;
reg            [7:0]        matrix_p21 , matrix_p22 , matrix_p23;
reg            [7:0]        matrix_p31 , matrix_p32 , matrix_p33;

reg            [9:0]        gx_temp1;
reg            [9:0]        gx_temp2;
reg            [9:0]        gx_data;

reg            [9:0]        gy_temp1;
reg            [9:0]        gy_temp2;
reg            [9:0]        gy_data;             

reg            [20:0]        gxy_square;
//--------------------------------
//Funtion :  移位

always @(posedge clk or negedge rst_n)
begin
    if(!rst_n)
    begin
        matrix_p11 <= 1'd0;
        matrix_p12 <= 1'd0;
        matrix_p13 <= 1'd0;
        matrix_p21 <= 1'd0;
        matrix_p22 <= 1'd0;
        matrix_p23 <= 1'd0;
        matrix_p31 <= 1'd0;
        matrix_p32 <= 1'd0;
        matrix_p33 <= 1'd0;        
    end
    else
    begin
        matrix_p11 <= gray;
        matrix_p12 <= matrix_p11;
        matrix_p13 <= matrix_p12;
        matrix_p21 <= matrix_p13;
        matrix_p22 <= matrix_p21;
        matrix_p23 <= matrix_p22;
        matrix_p31 <= matrix_p23;
        matrix_p32 <= matrix_p31;
        matrix_p33 <= matrix_p32;    
    end
end


//--------------------------------
//Funtion :  计算Gx Gy

always @(posedge clk or negedge rst_n)
begin
    if(!rst_n)
    begin
        gx_temp1 <= 1'd0;
        gx_temp2 <= 1'd0;
        gx_data     <= 1'd0;
    end
    else
    begin
        gx_temp1 <= matrix_p31 + (matrix_p32 << 1) + matrix_p33;
        gx_temp2 <= matrix_p11 + (matrix_p12 << 1) + matrix_p13;
        gx_data  <= (gx_temp1 >= gx_temp2) ? gx_temp1 - gx_temp2 : gx_temp2 - gx_temp1;
    end
end

always @(posedge clk or negedge rst_n)
begin
    if(!rst_n)
    begin
        gy_temp1 <= 1'd0;
        gy_temp2 <= 1'd0;
        gy_data     <= 1'd0;
    end
    else
    begin
        gy_temp1 <= matrix_p11 + (matrix_p21 << 1) + matrix_p31;
        gy_temp2 <= matrix_p13 + (matrix_p23 << 1) + matrix_p33;
        gy_data  <= (gy_temp1 >= gy_temp2) ? gy_temp1 - gy_temp2 : gy_temp2 - gy_temp1;
    end
end

//--------------------------------
//Funtion :  gx^2 + gy^2

always @(posedge clk or negedge rst_n)
begin
    if(!rst_n)
        gxy_square <= 1'd0;
    else
        gxy_square <= gx_data * gx_data + gy_data * gy_data;
end


//--------------------------------
//Funtion :  sqrt

sqrt_sobel sqrt_inst(
    .radical(gxy_square),
    .q(sobel_data),
    //remainder
    );






endmodule