线性规划(LP)问题的Matlab求解

华毓

已于 2022-09-29 18:13:56 修改

阅读量1.6w

点赞数 24

分类专栏： MATLAB完整学习过程优化问题

于 2022-09-23 01:38:35 首次发布

本文链接：https://blog.csdn.net/zhangkaikai36/article/details/126997190

版权

MATLAB完整学习过程同时被 2 个专栏收录

46 篇文章 86 订阅

订阅专栏

优化问题

4 篇文章 1 订阅

订阅专栏

Matlab求解线性问题LP（Liner programming）标准型

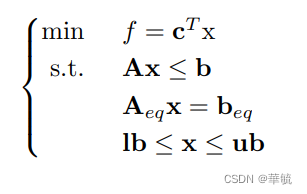
在这里插入图片描述
上述模型为用Matlab求解线性问题的标准型
1、模型由一个极小化的目标函数f，以及需要满足的约束条件构成。约束条件分为等式约束、不等式约束和边界约束。
2、假设决策变量x为n维的，且线性规划问题有m1个不等式约束，m2个等式约束。那么：c、x、lb和ub均为n维列向量，b为m1维列向量，beq为m2维列向量，A为m1×n维矩阵，Aeq为m2×n维矩阵。
ps：（关于c和x，因为矩阵相乘必须是前一个矩阵的列数等于后一个矩阵的行数，而向量都是用列向量来定义的。因而c和x必须是同维的列向量，向量C经过转置后变成n维的行向量，此时便可与n维列向量的x相乘了。）
（lb、ub与x一样也是n维的列向量，向量x大于等于向量xb，小于等于向量ub的意思是，拿向量x中的每个元素与向量lb和ub中的各个元素来做对比的）比如：

输出的结果为逻辑值。
（至于A、Aeq。如果有m1个不等式约束，那么A一定是一个m1行×n列的矩阵，因为矩阵相乘要求前一个矩阵的列等于后一个矩阵的行。比如说共有m1=4个不等式约束分别为ma、mb、mc和md，那么A的行数一定是m1=4，如下图）

 %ma、mb、mc、md为四个不等式约束，x为1行3列的向量
 ma=[1 2 3]; mb=[2 3 4]; mc=[3 4 5];md=[4 5 6]; x=[2;2;2]; 
 %分别将4个不等式约束与x相乘
 ba=ma*x  %表示1x1+2x2+3x3即第一个约束
 bb=mb*x  %表示2x1+3x2+4x3即第二个约束
 bc=mc*x  %表示3x1+4x2+5x3即第三个约束
 bd=md*x  %表示4x1+5x2+6x3即第四个约束
 %A为这四个约束集合一起组成的矩阵
 A=[ma;mb;mc;md]
 AX=m1*x

运行结果如下：
在这里插入图片描述
b为m1维列向量，A为m1×n维矩阵
Aeq与beq也是同理。

Matlab求解线性规划问题所要做的变换

在用Matlab求解线性问题标准型

1、MATLAB标准型是对目标函数求极小，如果遇到是对目标函数求极大的问题，在使用MATLAB求解时，需要在函数前面加一个负号转化为对目标函数求极小的问题；

2、MATLAB标准型中的不等式约束形式为“≤”，如果在线性规划问题中出现“≥”形式的不等式约束，则我们需要在两边乘以(-1)使其转化为MATLAB中的“≤”形式；

3、如果在线性规划问题中出现了“<”或者“>”的约束形式，则我们需要通过添加松弛变量使得不等式约束变为等式约束；
如果原有线性规划问题的约束条件为不等式，则可增加一个或减去一个非负变量，使约束条件变为等式，增加或减去的这个非负变量称为松弛变量。
4、之后，我们只需要将所有的约束（包括不等式约束和等式约束）转化为矩阵形式的即可。

Matlab求解线性规划

直接先来看一个简单的例子：
在这里插入图片描述
1、原问题为对目标函数求极大，故添加负号使变为：min f=-4x1+2x2-x3
2、原问题中存在“≥”的约束条件，故添加负号使其变为8x1-2x2+2x3≤-8
3、将约束整理为矩阵形式：

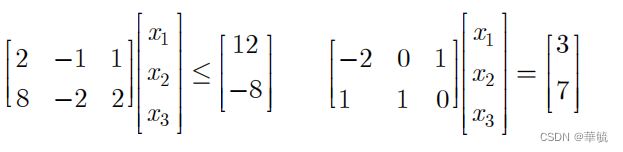
（将矩阵作以运算可以看出是：2x1-x2+x3≤12；8x1-2x2+2x3≤-8；-2x1+x3＝3；x1＋x2＝3。也就是上面的等式约束和不等式约束）

用Matlab表达为：

f=[-4; 2; -1]; %将目标函数转化为求极小
A=[2 -1 1; 8 -2 2]; b=[12; -8]; %不等式约束系数矩阵
Aeq=[-2 0 1; 1 1 0];beq=[3; 7]; %等式约束系数矩阵
lb=[0; 0; 0];ub=[Inf; Inf; Inf] %对设计变量的边界约束,上界和下界
x=linprog(f,A,b,Aeq,beq,lb,ub)

运行结果如下：
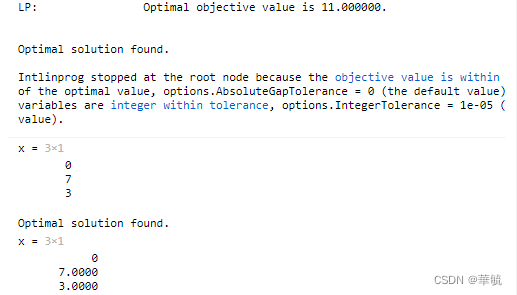
在这里插入图片描述

LP函数调用格式

MATLAB优化工具箱中求解线性规划问题的命令为linprog，其函数调用方法
有多种形式如下所示：

x = linprog(f,A,b)  %目标函数和不等式约束
x = linprog(f,A,b,Aeq,beq)  %目标函数、不等式约束和等式约束
x = linprog(f,A,b,Aeq,beq,lb,ub)  %目标函数、不等式约束、等式约束和边界约束
x = linprog(f,A,b,Aeq,beq,lb,ub,x0)  %目标函数、不等式约束、等式约束、边界约束和算法求解的初始点也就是迭代的初始点
x = linprog(c,A,b,Aeq,beq,lb,ub,x0,options)  %目标函数、不等式约束、等式约束、边界约束和算法求解的初始点也就是迭代的初始点、options是求解时用户提供的控制参量
x = linprog(problem)
[x,fval] = linprog(...)  %改变输出参数为两个，一个是x一个是f value，代表目标函数在x点处的目标函数值.
[x,fval,exitflag] = linprog(...)  %输出参数有三个
[x,fval,exitflag,output] = linprog(...)  %输出参数有四个
[x,fval,exitflag,output,lambda] = linprog(...)  %输出参数有五个

LP的输入参数

MATLAB工具箱中的linprog函数在求解线性规划问题时，提供的参数为：模
型参数、初始解参数和算法控制参数。

模型参数：x、f、A、b、Aeq、beq、ub、lb。决策变量、目标函数、不等式约束、等式约束和边界约束

x0为线性规划问题的初始解，该设置仅在中型规模算法中有效，而在默认的大型规模算法和单纯形算法中，MATLAB将忽略一切初始解。

options为包含算法控制参数的结构变量，我们可以通过optimset命令对这些具体的控制参数进行设置，例如下述格式options = optimset(‘param1’,value1,‘param2’,value2,…)
该命令格式创建一组控制参数结构变量options，将参数的具体值赋给单引号之间的参数，任何未被指定的参数将被赋值为[]，参数值为[]的具体的含义是将该组控制参数传递给优化函数时将使用MATLAB提供的默认值
在线性规划问题中可以用到的设置参数如下表所示：
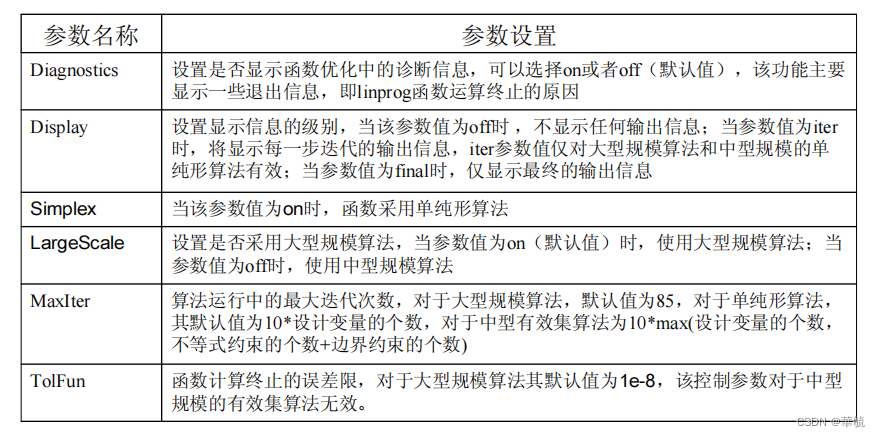
在这里插入图片描述

LP输入参数命令示例

1、x = linprog(f,A,b)
在这里插入图片描述
2、x = linprog(c,A,b,Aeq,beq)

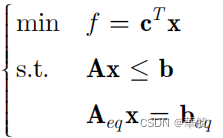
即该函数调用格式解决的是既含有线性等式约束，又含有线性不等式约束的线性规划问
题，如果在线性规划问题中无线性不等式约束，则可以设A=[]以及b=[]

3、x = linprog(c,A,b,Aeq,beq,lb,ub)
在这里插入图片描述
即在线性规划问题的求解过程中进一步考虑了对设计变量的约束，其中lb和ub均是和设
计变量维数相同的列向量，如果对设计变量没有上界约束，可以设置ub(i) = Inf，如果
没有下界约束则可以设置lb(i) = -Inf，和(2)类似，如果问题中没有等式约束，则可以设
Aeq=[]以及beq=[]

4、x = linprog(c,A,b,Aeq,beq,lb,ub,x0)
在前面调用方法的基础上设置线性规划问题求解的初始解为x0，该参数仅在使用有效集
算法时生效，否则当使用默认的内点算法时，将忽略任何初始点，即参数无效。

5、 x = linprog(c,A,b,Aeq,beq,lb,ub,x0,options)
用options指定的优化参数进行最小化。可以使用optimset来设置这些参数

LP的输出参数

linprog函数返回的输出参数有x、fval、exitflag、lambda和output。

1、输出参数x为线性规划问题的最优解
2、输出参数fval为线性规划问题在最优解x处的函数值
3、输出参数exitflag返回的是优化函数计算终止时的状态指示，说明算法终止的原因，其取值和其代表的具体原因如表所示：
在这里插入图片描述
4、输出参数output是一个返回优化过程中相关信息的结构变量，其属性如表所示：

5、输出参数lambda是返回线性规划问题最优解x处的拉格朗日乘子的一个结构变量,其总维数等于约束条件的个数，其非零分量对应于起作用的约束条件，其属性如表所示：
在这里插入图片描述

LP的输出参数的调用

1、[x,fval] = linprog(…)
在优化计算结束之时返回线性规划问题在解x处的目标函数值fval

2、 [x,fval,exitflag] = linprog(…)
在优化计算结束之时返回exitflag值，描述函数计算的退出条件。

3、 [x,fval,exitflag,output] = linprog(…)
在优化计算结束之时返回返回结构变量output

4、 [x,fval,exitflag,output,lambda] = linprog(…)
在优化计算结束之时返回线性规划问题最优解x处的拉格朗日乘子lambda

用Matlab求解线性规划的例子

如：
在这里插入图片描述

f=[-1;-1]; %目标函数，为转化为极小，故取目标函数中设计变量的相反数
A=[1 -2;1 2]; %线性不等式约束
b=[4;8];
lb=[0;0]; %设计变量的边界约束，由于无上界，故设置ub=[Inf;Inf];
ub=[Inf;Inf];
[x,fval]=linprog(f,A,b,[],[],lb,ub)

**加粗样式**
在这里插入图片描述

f=[-4;-3]; %目标函数，为转化为极小，故取目标函数中设计变量的相反数
A=[3 4;3 3;4 2]; %线性不等式约束
b=[12;10;8];
lb=[0;0]; %设计变量的边界约束，由于无上界，故设置ub=[Inf;Inf]
ub=[Inf;Inf];
[x,fval,exitflag]=linprog(f,A,b,[],[],lb,ub) %输出最优解x，在最优解x处的目标函数值f value，函数运行终止的状态指示变量

在这里插入图片描述

f=[-1;-3;1]; %目标函数，为转化为极小，故取目标函数中设计变量的相反数
Aeq=[1 1 2;-1 2 1]; %线性等式约束
beq=[4;4];
lb=[0;0;0]; %设计变量的边界约束，由于无上界，故设置ub=[Inf;Inf;Inf]
ub=[Inf;Inf;Inf];
[x,fval,exitflag,output]=linprog(f,[],[],Aeq,beq,lb,ub)%输出最优解x，在最优解x处的目标函数值f value，函数运行终止的状态指示变量,输出信息

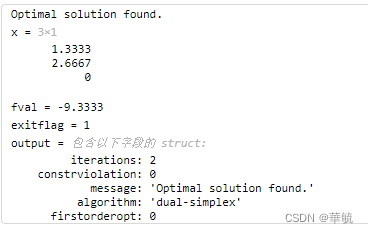
在这里插入图片描述
exitflag=1表示问题首先到了解x处
output里的参数可以对照上面的表

在这里插入图片描述

f=[-3;1;1]; %目标函数，为转化为极小，故取目标函数中设计变量的相反数
A=[1 -2 1;4 -1 -2]; %线性不等式约束
b=[11;-3];
Aeq=[-2 0 1]; %线性等式约束
beq=[1];
lb=[0;0;0]; %设计变量的边界约束，由于无上界，故设置ub=[Inf;Inf;Inf]
ub=[Inf;Inf;Inf];
[x,fval,exitflag,output,lambda]=linprog(f,A,b,Aeq,beq,lb,ub) %输出最优解x，在最优解x处的目标函数值f value，函数运行终止的状态指示变量，输出信息，线性规划问题最优解x处的拉格朗日乘子的一个结构变量