Sunday算法详解

一：背景

Sunday算法是Daniel M.Sunday于1990年提出的字符串模式匹配。其效率在匹配随机的字符串时比其他匹配算法还要更快。Sunday算法的实现可比KMP，BM的实现容易太多。

二：分析

假设我们有如下字符串：
A = "LESSONS TEARNED IN SOFTWARE TE";
B = "SOFTWARE";
Sunday算法的大致原理是：
先从左到右逐个字符比较，以我们的字符串为例：
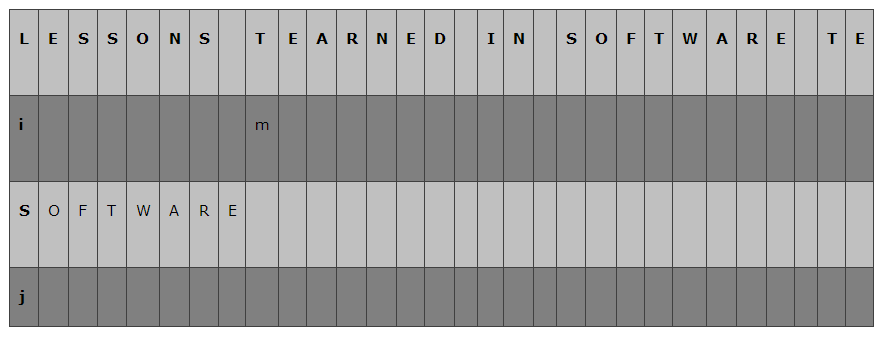
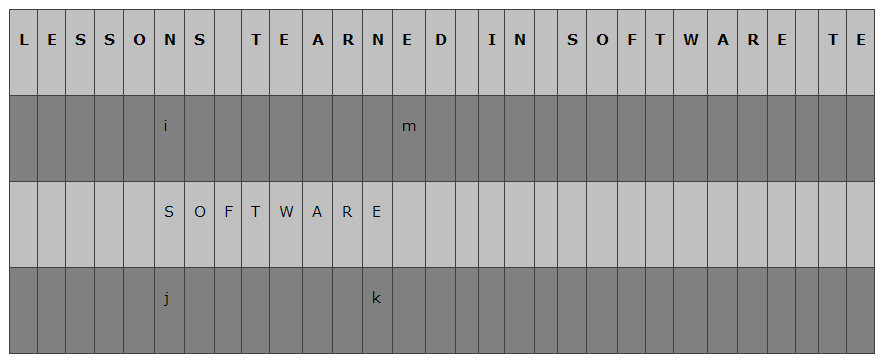
开始的时候，我们让i = 0, 指向A的第一个字符; j = 0 指向B的第一个字符，分别为"L"和"S"，不等；这个时候，Sunday算法要求，找到位于A字串中位于B字符串后面的第一个字符，即下图中 m所指向的字符"T"，在模式字符串B中从后向前查找是否存在"T"，

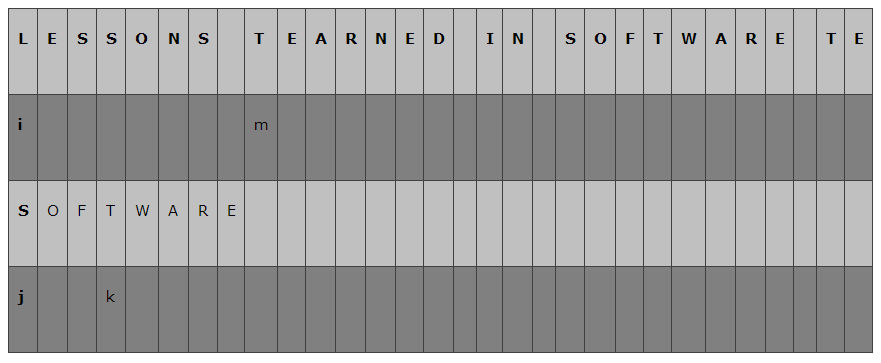
可以看到下图中k指向的字符与m指向的字符相等，

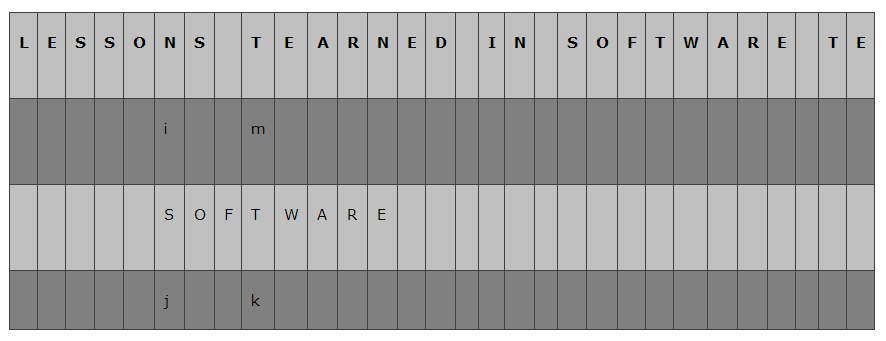
这时就将相等的字符对齐，让j再次指向B字符串的头一个字符，相应地，将i指向主串对应的字符N，

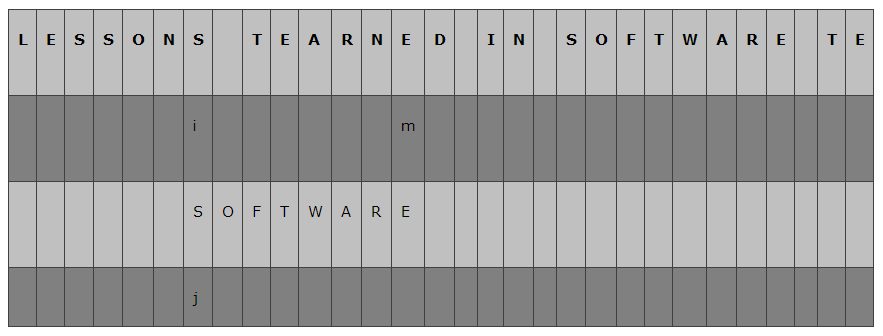
再次比较A[i]和B[j]，不等，这时再次寻找主串中在模式串后面的那个字符，

我们看到，模式串的最后一个字符与m指向的主串字符相等，因此再次移动子串，

这时，主串i对应的字符是S，j对应的子串字符也是S，i++, j++，

现在再次不等，m指向字符"D"，

三：完整代码

[cpp] view plain copy print ?

1. #define _CRT_SECURE_NO_DEPRECATE     
2. #define _CRT_SECURE_CPP_OVERLOAD_STANDARD_NAMES 1    
3.   
4. #include<iostream>   
5. #include<string>  
6.   
7. using namespace std;  
8.   
9. int _next[256];  
10. string dest;  
11. string pattern;  
12.   
13. /* 
14. 因为i位置处的字符可能在pattern中多处出现（如下图所示），而我们需要的是最右边的位置，这样就需要每次循环判断了，非常麻烦，性能差。这里有个小技巧，就是使用字符作为下标而不是位置数字作为下标。这样只需要遍历一遍即可，这貌似是空间换时间的做法，但如果是纯8位字符也只需要256个空间大小，而且对于大模式，可能本身长度就超过了256，所以这样做是值得的（这也是为什么数据越大，BM/Sunday算法越高效的原因之一）。 
15. */  
16. void GetNext()  
17. {  
18.     int len = pattern.size();//get the length  
19.   
20.     for (int i = 0; i < 256; i++)  
21.         _next[i] = -1;  
22.   
23.     for (int i = 0; i < len; i++)  
24.         _next[pattern[i]] = i;  
25. }  
26.   
27. int SundaySearch()  
28. {  
29.     GetNext();  
30.   
31.     int destLen = dest.size();  
32.     int patternLen = pattern.size();  
33.   
34.     if (destLen == 0) return -1;  
35.   
36.     for (int i = 0; i <= destLen - patternLen;)  
37.     {  
38.         int j = i;//dest[j]  
39.         int k = 0;//pattern[k]  
40.   
41.         for (; k<patternLen&&j < destLen&&dest[j] == pattern[k]; j++, k++)  
42.             ;//do nothing  
43.   
44.         if (k == patternLen)//great! find it!  
45.             return i;  
46.         else  
47.         {  
48.             if (i + patternLen < destLen)  
49.                 i += (patternLen - _next[dest[i + patternLen]]);  
50.             else  
51.                 return -1;  
52.         }  
53.     }  
54.   
55.     return -1;  
56. }  
57.   
58. int main()  
59. {  
60.     dest = "This is a wonderful city";  
61.       
62.     //case one(successful locating)  
63.     pattern = "wo";  
64.     int result = SundaySearch();  
65.     if (result == -1)  
66.         cout << "sorry,you do not find it!\n";  
67.     else  
68.         cout << "you find it at " << result << endl;  
69.   
70.     //case two(unsuccessful locating)  
71.     pattern = "wwe";  
72.     result = SundaySearch();  
73.     if (result == -1)  
74.         cout << "sorry,you do not find it!\n";  
75.     else  
76.         cout << "you find it at" << result << endl;  
77.   
78.     return 0;  
79. }  

测试：