二叉树的遍历 C++模板+封装

最新推荐文章于 2024-09-19 00:41:25 发布
最新推荐文章于 2024-09-19 00:41:25 发布
阅读量1.9k 收藏 9
点赞数 2
分类专栏： 数据结构与算法分析 文章标签： 二叉树 C++ 遍历 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/zhangxiao93/article/details/52734630
版权

二叉树的遍历主要是前序、中序和后序遍历（还有层序遍历，参见：层序遍历）

（一）递归形式

这三种遍历访问顺序分别为：

前序：根->左子树->右子树
中序：左子树->根->右子树
后序：左子树->右子树->根

递归的形式来写非常简单，伪代码如下：

//前序遍历
void PreOrder(TreeNode *root)
{
    if (root == NULL)
        return;
    Visit root->val;
    PreOrder(root->left);
    PreOrder(root->right);
}

//中序遍历
void InOrder(TreeNode *root)
{
    if (root == NULL)
        return;
    InOrder(root->left);
    Visit root->val;
    InOrder(root->right);
}

//后序遍历
void PostOrder(TreeNode *root)
{
    if (root == NULL)
        return;
    PostOrder(root->left);
    PostOrder(root->right);
    Visit root->val;
}

（二）非递归形式

非递归形式主要利用栈来实现各种顺序遍历时节点的访问顺序。

2.1非递归先序遍历

1.对于节点P，只要左子树不为空，就一直向左访问，并将访问的节点压栈。
2.当左子树为空时，另P指向栈顶元素的右节点并弹栈，执行步骤1。

void PreOrderNonRescursion(TreeNode *root)//伪代码
{
    NodeType *p=root;
    stack<NodeType*>s;
    while(NULL!=p || !s.empty())
    {
        while(NULL!=p)
        {
            s.push(p);
            visit p->val;
            p=p->left;
        }
        if(!s.empty())
        {
            p=s.top();
            s.pop();
            p=p->right;
        }
    }
}

2.2非递归中序遍历

与先序遍历类似。
1.对于节点P，只要左子树不为空，就一直向左压栈（但不访问）
2.当左子树为空时，访问栈顶元素，并另P指向栈顶元素的右子树，弹栈，执行步骤1。

template <typename T>
void InOrderNonRescursion(TreeNode*root)//伪代码
{
    NodeType *p=root;
    stack<NodeType*>s;
    while(NULL!=p || !s.empty())
    {
        while(NULL!=p)
        {
            s.push(p);
            p=p->left;
        }
        if(!s.empty())
        {
            p=s.top();
            visit p->val
            s.pop();
            p=p->right;
        }
    }
}

2.3非递归后序遍历

这个就相对复杂了。要保证在访问当前节点Cur之前，
1.要么Cur不存在左右孩子，即左右子树为NULL。
2.要么Cur的左右孩子已经被访问过了，Pre节点不为NULL且为Cur节点的左右孩子之一。

否则，如果不满足上述条件，说明当前Cur节点的左右孩子还没有被访问，那么为了保证先左子树在右子树的访问顺序，我们要先将右子树压栈，再将左子树压栈（如果不为空的话。）

结合上述条件有：

void Tree<T>::PostOrderNonRescursion(NodeType*root)//伪代码
{
    NodeType *pre=NULL;
    //NodeType *cur=root;
    NodeType *cur;
    stack<NodeType*>s;
    s.push(root);
    while( !s.empty())
    {
        cur=s.top();
        if( ((cur->left==NULL)&&(cur->right==NULL))|| //左右子树为空
            (pre!=NULL&&(pre==cur->left||pre==cur->right)) )//或者左右子树已被访问
        {
            //visit cur
            s.pop();
            pre=cur;
        }
        else
        {
            if(cur->right!=NULL)
                s.push(cur->right);
            if(cur->left !=NULL)
                s.push(cur->left);
        }
    }
}

（三）二叉树的封装

假期无聊。想了想，就把上述三种遍历递归和非递归形式用模板封装了下。

3.1数据结构

//TreeNode.h

#ifndef __TREENODE_H__
#define __TREENODE_H__
#include "Tree.h"
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
template <typename T> class Tree;
template <typename T>
class TreeNode
{
    friend class Tree<T>;
    private:
        T val;
    public:
        TreeNode<T>*left;
        TreeNode<T>*right;

        TreeNode():val(0),left(NULL),right(NULL){}
        TreeNode(T x):val(x),left(NULL),right(NULL){}
};
#endif

3.2二叉树的封装

#ifndef __TREE_H__
#define __TREE_H__
#include "TreeNode.h"
using namespace std;

template <typename T> class TreeNode;


template  <typename T>
class Tree
{

    typedef TreeNode<T> NodeType;
    private:
        NodeType *root;
        void PreOrder_(NodeType *,vector<T>&);
        void InOrder_(NodeType *,vector<T>&);
        void PostOrder_(NodeType *,vector<T>&);
        void PreOrderNonRescursion_(NodeType *,vector<T>&);
        void InOrderNonRescursion_(NodeType *,vector<T>&);
        void PostOrderNonRescursion_(NodeType *,vector<T>&);
        void DestroyAllNode_(NodeType *);
    public:
        Tree(NodeType * r){root=r;}
        ~Tree();
        void PreOrder(vector<T>&);
        void InOrder(vector<T>&);
        void PostOrder(vector<T>&);
        void PreOrderNonRescursion(vector<T>&);
        void InOrderNonRescursion(vector<T>&);
        void PostOrderNonRescursion(vector<T>&);

};

//constructor and destructor//
template <typename T>
void Tree<T>::DestroyAllNode_(NodeType*root)
{
    if(root==NULL)
        return ;
    DestroyAllNode_(root->left);
    DestroyAllNode_(root->right);
    delete root;
    root=NULL;
    return ;
}

template <typename T>
Tree<T>::~Tree()
{
    DestroyAllNode_(root);
}
/PreOrder Traversal//
template <typename T>
void Tree<T>::PreOrder_(NodeType*root,vector<T>&res)
{
    if(root==NULL)
    {
        return;
    }
    res.push_back(root->val);
    PreOrder_(root->left,res);
    PreOrder_(root->right,res);
}

template <typename T>
void Tree<T>::PreOrder(vector<T>&res)
{
    PreOrder_(root,res);
}

template <typename T>
void Tree<T>::PreOrderNonRescursion_(NodeType*root,vector<T>&res)
{
    NodeType *p=root;
    stack<NodeType*>s;
    while(NULL!=p || !s.empty())
    {
        while(NULL!=p)
        {
            s.push(p);
            res.push_back(p->val);
            p=p->left;
        }
        if(!s.empty())
        {
            p=s.top();
            s.pop();
            p=p->right;
        }
    }
}
template <typename T>
void Tree<T>::PreOrderNonRescursion(vector<T>&res)
{
    PreOrderNonRescursion_(root,res);
}

//InOrder Traversal///
template <typename T>
void Tree<T>::InOrder_(NodeType*root,vector<T>&res)
{
    if(root==NULL)
    {
        return;
    }
    InOrder_(root->left,res);
    res.push_back(root->val);
    InOrder_(root->right,res);
}

template <typename T>
void Tree<T>::InOrder(vector<T>&res)
{
    InOrder_(root,res);
}

template <typename T>
void Tree<T>::InOrderNonRescursion_(NodeType*root,vector<T>&res)
{
    NodeType *p=root;
    stack<NodeType*>s;
    while(NULL!=p || !s.empty())
    {
        while(NULL!=p)
        {
            s.push(p);
            p=p->left;
        }
        if(!s.empty())
        {
            p=s.top();
            res.push_back(p->val);
            s.pop();
            p=p->right;
        }
    }
}
template <typename T>
void Tree<T>::InOrderNonRescursion(vector<T>&res)
{
    InOrderNonRescursion_(root,res);
}

/PostOrder Traversal
template <typename T>
void Tree<T>::PostOrder_(NodeType*root,vector<T>&res)
{
    if(root==NULL)
    {
        return;
    }
    PostOrder_(root->left,res);
    PostOrder_(root->right,res);
    res.push_back(root->val);
}

template <typename T>
void Tree<T>::PostOrder(vector<T>&res)
{
    PostOrder_(root,res);
}

template <typename T>
void Tree<T>::PostOrderNonRescursion_(NodeType*root,vector<T>&res)
{
    NodeType *pre=NULL;
    //NodeType *cur=root;
    NodeType *cur;
    stack<NodeType*>s;
    s.push(root);
    while( !s.empty())
    {
        cur=s.top();
        if( ((cur->left==NULL)&&(cur->right==NULL))||
            (pre!=NULL&&(pre==cur->left||pre==cur->right)) )
        {
            res.push_back(cur->val);
            s.pop();
            pre=cur;
        }
        else
        {
            if(cur->right!=NULL)
            s.push(cur->right);
            if(cur->left !=NULL)
            s.push(cur->left);
        }
    }
}
template <typename T>
void Tree<T>::PostOrderNonRescursion(vector<T>&res)
{
    PostOrderNonRescursion_(root,res);
}

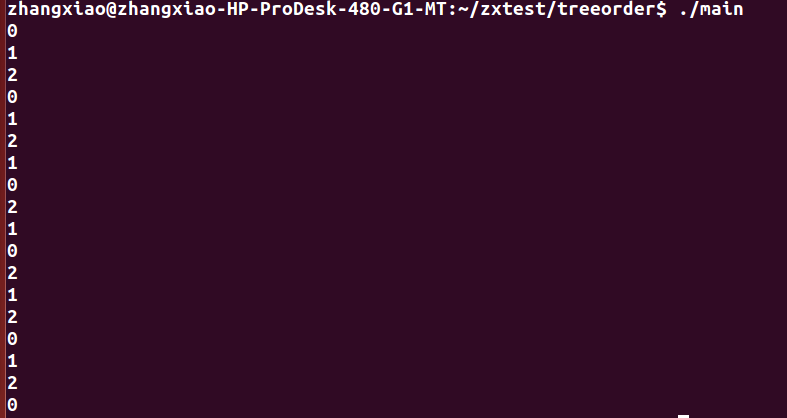
#endif

3.3测试

//main.cpp

#include "Tree.h"
int main()
{
    TreeNode<int> *root=new TreeNode<int>(0);
    root->left=new TreeNode<int>(1);
    root->right=new TreeNode<int>(2);

    Tree<int> t(root);

    vector<int>res;
    t.PreOrder(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }

    res.clear();
    t.PreOrderNonRescursion(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }

    res.clear();
    t.InOrder(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }

    res.clear();
    t.InOrderNonRescursion(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }

    res.clear();
    t.PostOrder(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }

    res.clear();
    t.PostOrderNonRescursion(res);
    for(int i=0;i<res.size();i++)
    {
        cout << res[i];
        cout <<endl;
    }


    return 0;
}

这里写图片描述

（四）参考

1.http://www.cnblogs.com/dolphin0520/archive/2011/08/25/2153720.html

mfc c++ 二叉树图形界面 遍历
11-17
在MFC中，你可以利用C++的面向对象特性，为每种遍历方式创建一个成员函数，或者封装成一个通用的遍历函数，通过参数指定遍历类型。同时，为了实现图形界面的动态更新，你可能需要使用消息队列和事件驱动编程，当用户...
C++二叉树及遍历方式
qq_49209946的博客
03-16 1310
PS：前中后序的递归版本代码非常的简单，所以如果有能力的情况下，最好还是学会迭代版本，其原理是利用了栈结构的先入后出的原则，实现了前中后序遍历，而层序遍历则利用了队列的先入先出原则实现，这个需要特别的注意一下，上面的代码可以直接当做模板。其中层序遍历最好理解，就是将二叉树从根节点向下，一层一层遍历出来，遍历出来的结果就是一个二维数组，一维长度就是数的高度，二维长度就是每层的节点的个数。（有一个很好记的方法，就是记根节点的位置，在前就是前序，在中就是中序，在后就是后续，因为左右的相对顺序是不会变的）
C++ 二叉树模板
fulianzhou的专栏
06-23 897
#include "stdafx.h" #include using namespace std; /* 结构体结点 */ template struct TNode{ TNode* lchild; TNode* rchild; T data; TNode(TNode* ptr = NULL){ lchild = rchild = ptr; } TNode(T item, TNod
二叉树的遍历【C++】
最新发布
xaiobai123的博客
09-19 522
对于二叉树系列的题，必须要会二叉树。什么序是指处理根节点在哪个位置，比如前序是指处理节点顺序：根左右。接下来要说明的是：选用实现还是实现，一般来说递归法和迭代法可以相互转化。常常使用栈或者队列来实现。
二叉树类模板-C++实现
m0_55464171的博客
05-18 2080
二叉树是一种重要的数据结构，本文将用C++实现二叉树及其一些基本操作：遍历，插入，删除，查找…… 1）定义二叉树的模板类，并声明一些方法 template<class T> class tree { private: struct TreeNode; //树的结点 typedef TreeNode*NodePtr; static T out_of_range; //防止迭代器越界的静态变量 protected: NodePtr _root; //根结点 public: class
C++实现的二叉树模板及其应用实例
weixin_42898801的博客
05-10 210
用c++语言实现了二叉树模板类， 并用Qt新建控制台工程，演示了二叉树模板类的使用
二叉树（C++模板实现）
qq_39559641的博客
04-07 5142
一、实验要求 <1>打印出二叉树的三种遍历序。 <2>设计算法按中序次序输出二叉树中各结点的值及其所对应的层次数。 <3>求二叉树的高度。 <4>求二叉树的结点数。 <5>求二叉树的叶子结点数。 <6>求二叉树的度为2的结点数。 <7>键盘输入一个...
二叉树的类封装（C++）
01-18
本篇将详细介绍如何用C++语言进行二叉树的类封装，包括数组实现和链表实现，以及它们的常用操作。 首先，我们需要定义一个二叉树节点类。对于链表实现，节点类通常包含数据成员（存储节点值）、指向左子节点的指针...
二叉树的C++实现
07-10
本文将深入探讨如何使用C++来实现二叉树，包括其基本操作以及四种常见的遍历方法。 首先，为了在C++中表示二叉树，我们需要定义一个名为`Node`的结构体或类，它包含一个值（通常是整数或其他数据类型）以及指向左右...
二叉树-基于C++实现的平衡二叉树.zip
04-26
在计算机科学中，二叉树是一种特殊的树结构，其中每个...此外，还需要掌握二叉树的基本操作，如前序、中序和后序遍历，以及平衡调整算法。通过阅读和分析提供的源代码，你可以进一步提升在数据结构和算法方面的技能。
二叉排序树模板类c++
02-03
在给定的部分代码中，首先定义了一个模板结构体`BiNode`用于表示二叉排序树中的节点，以及一个模板类`BiSortTree`用于封装二叉排序树的各种操作。 ```cpp template struct BiNode { T data; // 节点存储的数据 ...
数据结构中二叉树的模板实现c++,基本上二叉树所有的操作都有了
12-24
前序中序后序的递归遍历,游标类的非递归遍历,复制树,求深度,重载==,<<,!,交换子树,层次遍历都用模板实现了,栈和队列用的是以前自己写的模板 程序的输入是数组,通过二叉树的数组表示创建的链表表示的二叉树,输出没有做成树型输出,感觉太复杂,而是按照广义表的输出方式输出 写的时候感觉大部分的操作实现都很简单,不过非递归方式的后序和中序的游标遍历搞的比较头疼!
C++二叉树的类模板
05-10
C++二叉树模板，包含了基本的二叉树的操作。
二叉树-基于C++实现的二叉搜索树.zip
04-26
查找操作同样从根节点开始，根据节点值的大小关系进行比较，直到找到目标节点或者遍历完所有节点。删除操作相对复杂，可能需要考虑三种情况：删除的节点没有子节点、有一个子节点和有两个子节点。 ```cpp class BST...
二叉树的C++非递归实现
11-17
**先序遍历**是二叉树遍历的一种，顺序为：根节点 -> 左子树 -> 右子树。非递归实现通常使用栈来辅助完成。首先访问根节点，然后将右子节点压入栈中，接着访问左子节点。当没有左子节点时，从栈顶取出节点并检查其右...
树及二叉树(C++版).ppt
07-11
《树及二叉树(C++版)》的讲解主要涵盖了树型数据结构的基本概念和二叉树的应用。树作为一种非线性的数据结构，其特点在于能够有效地表达具有分支和层次特征的数据集合。在计算机科学中，树的应用广泛，如在编译器中...
二叉树(C++类模板实现)
zws的博客
11-21 4305
文章目录1. 二叉树的定义2.二叉树的性质3.二叉树的存储结构4. 代码 1. 二叉树的定义 后续更新 2.二叉树的性质 后续更新 3.二叉树的存储结构 顺序存储结构。顺序存储结构使用一组地址连续的存储单元来存储数据元素，为了能够在存储结构中反映出结点之间的逻辑关系，必须将二叉树中的结点依照一定的规律安排在这组单元中。 链式存储结构设计不同的结点结构可构成不同形式的链式存储结构。由二叉树的定义得知，二叉树的结点由一个数据元素和分别指向其左、 右子树的两个分支构成，则表示二叉树的链表 中的结点至少
C++模板实现二叉树
程序猿老樊的博客
08-27 1232
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。       二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有2^{i-1}个结点；深度为k的二叉树至多有2^k-1个结点；对任何一棵二叉树T，如果其终端结
二叉树-遍历（CPP实现简单易懂图解解法很全）
CODER-GODV的博客
10-21 789
准备一个栈容器，先对根结点一直向左迭代，并每次将其入栈，直到访问到空结点，然后将当前结点设置为栈顶的一个结点，如果它的右结点为空或者已经访问过，就访问当前元素， 并把它移出栈，将当前结点设置为空，以便访问上一个结点，反复如此，直到当前结点和栈为空，退出循环，即后续遍历完成。先准备一个栈，依次从根节点一直向左下前进，直到发现当前节点为空，然后从栈中弹出一个节点，先访问自己，然后再访问它的右子节点，一直迭代这过程，直到当前节点为空节点， 并且此时栈为空，即中序遍历完成。基线条件：当节点为空时，返回空。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值