【概念梳理】激活函数

一、引言

常用的激活函数如下：
1、Sigmoid函数
2、Tanh函数
3、ReLU函数
4、ELU函数
5、PReLU函数
6、Leaky ReLU函数
7、Maxout函数
8、Mish函数

二、激活函数的定义

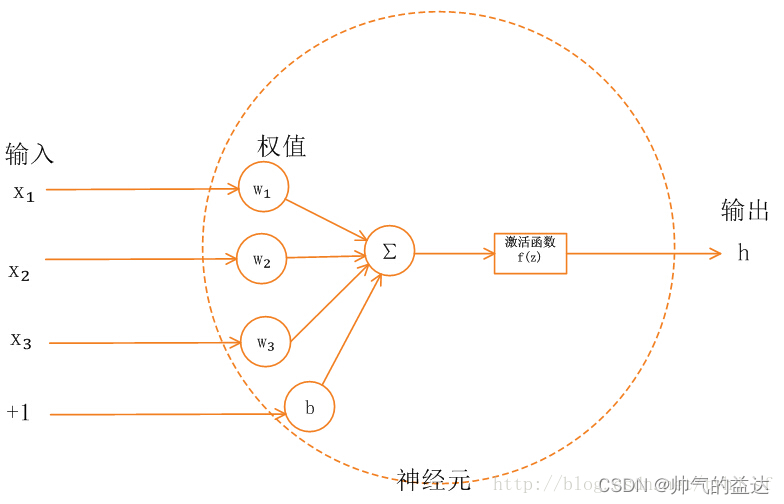
多层神经网络中，上层节点的输出和下层节点的输入之间具有一个函数关系，这个函数称为激活函数（Activation Function）。

三、激活函数的作用

一句话总结：为了提高模型的表达能力。
激活函数能让中间输出多样化，从而能够处理更复杂的问题。如果不使用激活函数，那么每一层的输出都是上一层输入的线性函数，最后的输出也只是最开始输入数据的线性组合而已。而激活函数可以给神经元引入非线性因素，当加入到多层神经网络时，就可以让神经网络拟合任何线性函数或非线性函数，从而使得网络可以适合更多的非线性问题，而不仅仅是线性问题。
激活函数被定义为一个几乎处处可微的函数。

四、饱和的概念

当函数满足$li{m}_{x\to +\infty }{f}^{\prime }(x)=0$时，称为右饱和；
当函数满足$li{m}_{x\to -\infty }{f}^{\prime }(x)=0$时，称为左饱和；
当$f(x)$同时满足左饱和和右饱和时，称为饱和

在饱和定义的基础上，如果存在常数$C1$，当$x>C1$时，恒满足$f^{\prime }(x)=0$，称为右硬饱和；同样，如果存在常数$C2$，当$x<C2$时，恒满足$f^{\prime }(x)=0$，称为左硬饱和

相对的，只有当$x$趋于极值时，$f^{\prime }(x)=0$，则称为软饱和。

五、常用的激活函数

1、Sigmod函数

Sigmoid 是常用的非线性的激活函数，它的数学形式如下：
$f(x)=\frac{1}{1+e^{-x}}$

Sigmoid的几何图像如下：

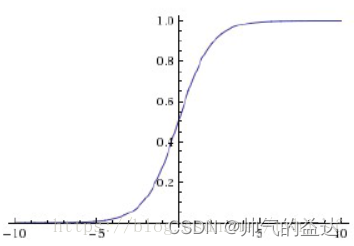
特点：
它能够把输入的连续实值映射为0和1之间的输出，特别的，如果是非常大的负数，输出就是0；如果是非常大的正数，输出就是1。
优点：
（1）单调递增，容易优化；
（2）求导容易。
缺点：
（1）Sigmod函数是软饱和，容易产生梯度消失；
（2）求导收敛速度慢；
（3）幂运算导致训练耗时。

Sigmod函数导数如下：
$f^{\prime }(x)=f(x)(1-f(x))$

导数的集合图像

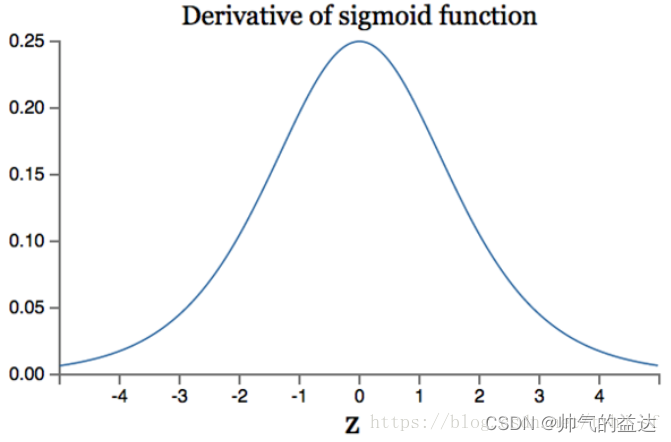
2、Tanh函数

tanh函数为双切正切函数，过$(0,0)$点，数学形式如下：

$f^{\prime }(x)=\frac{sinh(x)}{cosh(x)}=\frac{1-e^{-2x}}{1+e^{-2x}}=\frac{e^x-e^{-x}}{e^x+e^{-x}}=\frac{e^{2x}-1}{e^{2x}+1}=2Sigmod(x)-1$

tanh函数及其导数的几何图像如下图：

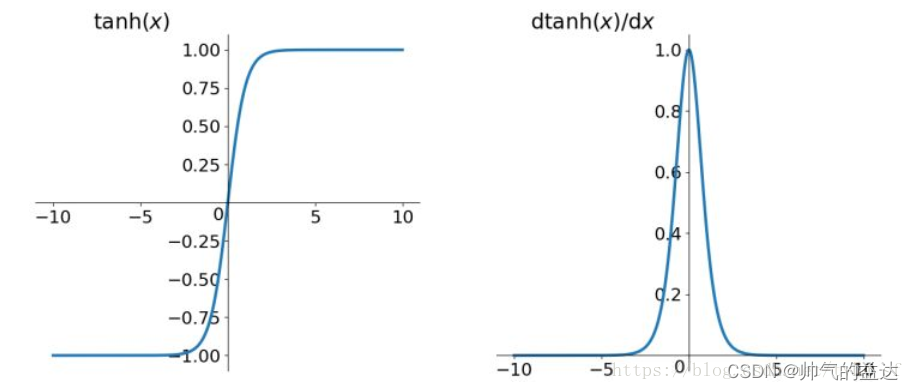
tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是零均值（zero-centered）输出的问题。然而，梯度消失（gradient vanishing）的问题和幂运算导致的耗时问题仍然存在。
优点：
（1）收敛速度相比Sigmod快
缺点：
（1）未能解决梯度消失的问题

问题1：什么是零均值化（zero-centered）？
对所有输入数据进行预处理，计算训练数据中每组数据的均值，然后每组数据的值减去对应的均值。零均值化后的数据以$(0,0)$为中心，所有数据的均值为0。

问题2：为什么要对数据零均值化（zero-centered）？
一句话总结：为了在反向传播中加快网络中每一层权重参数的收敛。
假设图中蓝色箭头方向理想最优$w$向量，当$x$全为正或者全为负时，每次返回的梯度都只会沿着一个方向发生变化，即梯度变化的方向就会向图中红色箭头所示，一会向上太多，一会向下太多。这样就会使得权重收敛效率很低。但当$x$正负数量“差不多”时，就能对梯度变化方向进行“修正”，使其接近上图中蓝色箭头的方向，加快了权重的收敛。

3、ReLU函数

ReLU函数的数学形式如下：
$f(x)=max(0,x)=\{\begin{array}{ll}0,& x\le 0\\ x,& x>0\end{array}$

ReLU函数及其导数的几何图像如下图：

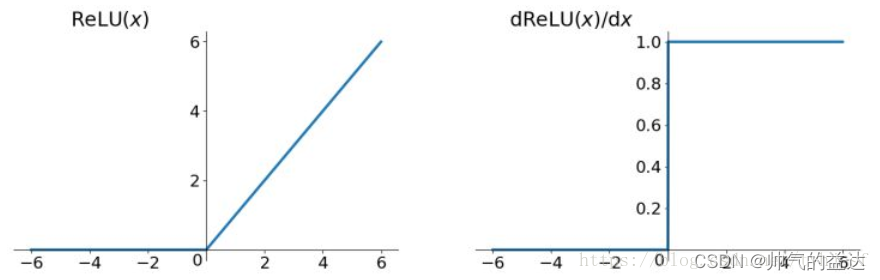
优点：
（1）收敛速度快与Sigmod函数和Tanh函数；
（2）有效缓解了梯度消失问题（在正区间）；
（3）训练耗时优于Sigmod函数和Tanh函数；
（4）对神经网络可以使用稀疏表达；
缺点：
（1）在训练过程中容易出现神经元死亡（Dead ReLU Problem），之后梯度永远为0。
产生该问题的原因有两点：
（1）非常不幸的参数初始化，这种情况比较少见；
（2）学习率（learning rate）太大导致在训练过程中参数更新幅度太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将学习率设置太大或使用adagrad等自动调节学习率的优化算法。

4、ELU函数

ELU函数（Exponential Linear Units）的数学形式如下：
$f(x)=max(\alpha (e^x-1),x)=\{\begin{array}{ll}x,& x>0\\ \alpha (e^x-1),& x\le 0\end{array}$
其中，$\alpha$是可学习的参数。

ELU函数及其导数的几何图像如下图：

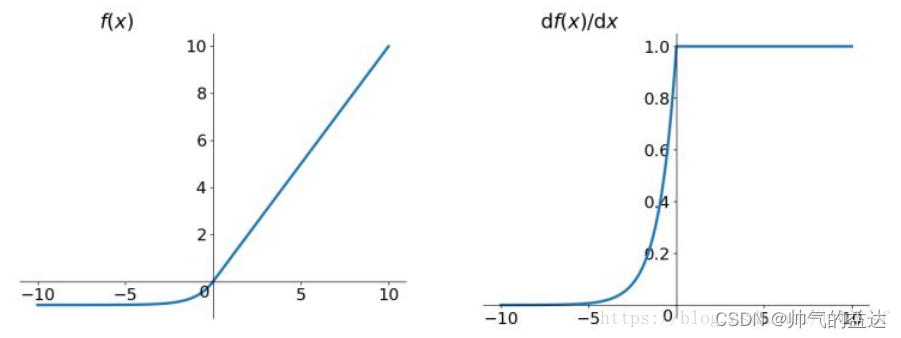
优点：
（1）ELU是为解决ReLU存在的问题而提出，显然，ELU有ReLU的基本所有优点，并可以消除ReLU中神经元死亡问题，在输入为负数时，具有一定输出，而且这部分输出具有一定的抗干扰能力。
缺点：
（1）幂运算增加了训练耗时。

5、PReLU函数

PReLU函数的数学形式如下：
$f(x)=max(\alpha x,x)=\{\begin{array}{ll}x,& x>0\\ \alpha x,& x\le 0\end{array}$
其中，$\alpha$是可学习的参数。

优点：
（1）相比于ELU函数，PReLU函数在负数区域是线性的，斜率虽小，但不会趋于0，因为没有了幂运算，训练速度也会快一些。

6、Leaky ReLU函数

Leaky ReLU函数的数学形式如下：
$f(x)=max(0.01x,x)=\{\begin{array}{ll}x,& x>0\\ 0.01x,& x\le 0\end{array}$

Leaky ReLU函数及其导数的几何图像如下图：

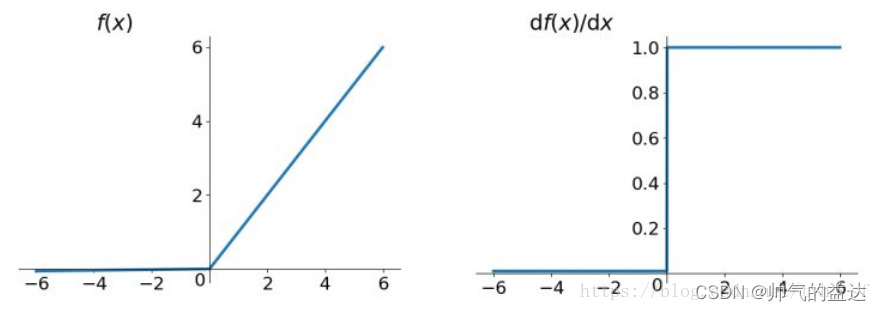
相比于PReLU函数，当$\alpha$为0.01时，PReLU函数就变成了Leaky ReLU函数了。

7、Maxout函数

待更新

8、Mish函数

Leaky ReLU函数的数学形式如下：
$f(x)=x\ast tanh(l{n}^{(1+e^x)})$

Mish函数及其导数的几何图像如下图：

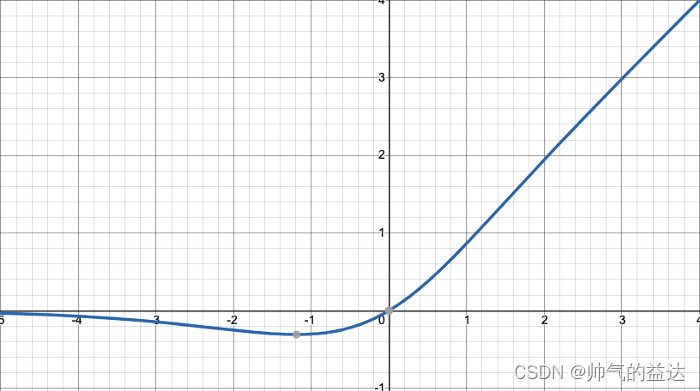
这与另一个被称为Swish函数的激活函数非常相似，Swish函数的数学形式如下：
$f(x)=x\ast Sigmoid(x)$

Swish函数及其导数的几何图像如下图：

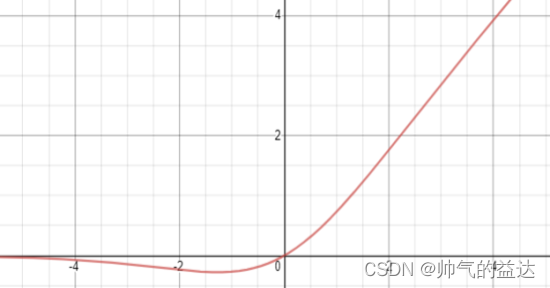
Mish函数是YOLOv4中使用的激活函数，原因是它的低成本和它的平滑、非单调、上无界、有下界等特点。

Mish函数的性能详细说明如下：
（1）无上界有下界：无上界是任何激活函数都需要的特性，因为它避免了导致训练速度急剧下降的梯度饱和，可加快训练过程。有下界属性有助于实现强正则化效果，适当的拟合模型（Mish的这个性质类似于ReLU和Swish的性质，其范围是$(\approx 0.31,+\infty ]$)；
（2）非单调函数：这种性质有助于保持小的负值，从而稳定网络梯度流。大多数常用的激活函数，如ReLU、 Leaky ReLU，由于其差分为0，不能保持负值，因此大多数神经元没有得到更新；
（3）无穷阶连续性和光滑性：Mish是光滑函数，具有较好的泛化能力和结果的有效优化能力，可以提高结果的质量。在图中，可以看到ReLU和Mish之间的一个随机初始化的神经网络在宏观平滑度上的剧烈变化。然而，在Swish和Mish的情况下，宏观上或多或少还是相似的；

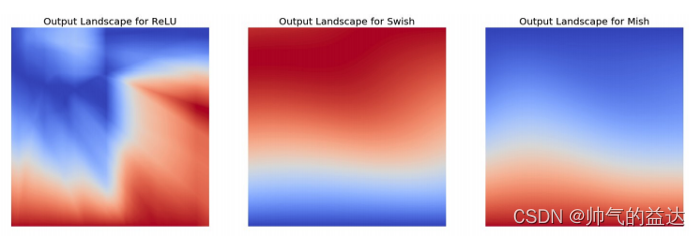
（4）计算量较大，但是效果更好：与ReLU相比，它的计算量比较大，但在深度神经网络中显示了比ReLU更好的结果。
（5）自门控：此属性受到Swish函数的启发，其中标量输入被提供给gate。它优于像ReLU这样的点式激活函数，后者只接受单个标量输入，而不需要更改网络参数。

参考资料

1、常用激活函数（激励函数）理解与总结
2、YOLOv4 中的 Mish 激活函数

声明

本博客的目的仅为学习交流和记录，谢谢大家的浏览。