Bloom Filter 系列改进之Bloom Tree

bloom tree的设计:

    如果对bloom filter不是很了解，请参看我之前写过的blog。

    bloom tree 是一个d叉完全树,存储的是一个个(key,value)键值对，bloom tree支持近似的表格查询，当一个被查询元素的key被给出时，bloom tree会在一定的可能性下给出正确的值，一个特别的特点是bloom tree是由value构建的，不像传统的搜索树都是用key构建的。

    bloom tree 的适用范围是：键值对的数据存储，即一个key对应一个value类型的，这种数据的查询和查找采用bloom tree 将会得到很好的效果。

    bloom tree中的每一个树枝节点都是一个bloom filter；每一个内部节点都拥有d个独立的bloom filter，或者说拥有d组相互独立的hash函数集，每个bloom filter对应从其出发的一条分支。在查找时，如果一个集合中的所有hash函数，散列后的值都为1，那么我们沿着该分支方向向下继续检查。

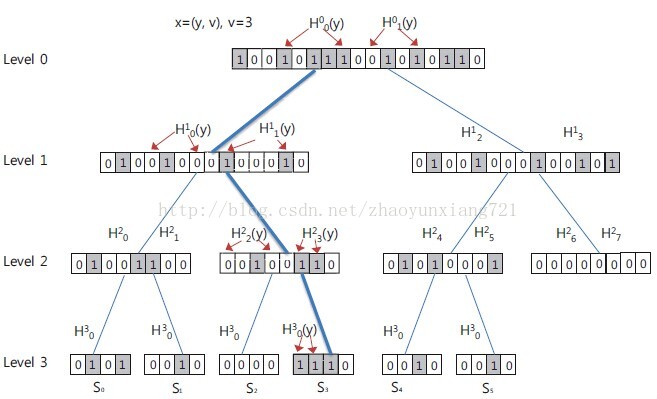
    现在假设我们构建一个满足{m,g,pf,pc}的bloom tree，首先需要构建一个拥有g个树枝节点的d叉树，假设g是d的方幂，那么该树的高度为：l = logd(g)，如果g不是d的方幂，那么树的高度为：l = ⌈logd(g)⌉，同时选择树枝节点中的前g个来表示这些元素，如下图所示，d=2，g=6。

    我们假设在同一层的各个节点拥有相同大小的位数组,它们含有的hash函数的个数也相同,分别用mi和ki表示.

 bloom tree的编码

    假设现在有一个新的元素x=(y,v)需要加入到集合中，其中y是元素x的key，v是元素x的value，在bloom tree中，元素从根节点到叶子节点的路径是由他的value决定的，即元素x中的v。在编码过程中，每一层都会在其拥有的d个hash函数集和中选取一个集合，然后用这个集合中含有的所有hash函数对y进行hash，然后将得到的数值作为下标，对位数组进行置位为1。上图中给出的例子就是很好的解释，可以看出在每一层的位数组，随机选择了一组hash函数对y进行hash，然后将结果对应的位数组编号进行置1操作，直到到达叶子节点为止。由于在每一层都选取了ki个hash函数，所以进行一次插入操作需要的访存次数为k0+k1+...+ki.

bloom tree的查找

    给定一个元素的key值y，那么从根节点向下依次进行判断，在每一层，用该层拥有的d个hash集合分别对y进行hash，如果存在一个hash集合使得得到的结果对应的位数组都是1，那么说明该元素还有继续查询的可能，下一步到达的分支就是那个全是1那个hash集合对应的分支，然后依次判断直到到达叶子节点后得到想要的元素，或者是无法进行下去了。

    对于无法进行下去的情况，这里有两种可能，一种是确实找不到该元素，另一种是存在了冲突导致该元素没有按照正确的分支走下去，这种情况的产生是因为在某个分支中，共有d个hash函数集和，本来该元素应该在第j个hahs集合对应的分支下面，但是由于在j前面的hash集合对y进行hash得到的结果同样达到了对应位数组的位置全是1，于是他步入歧途...

   (未完待续，原理解释清楚了，但是细节有感兴趣的可以自己看看原文,感觉这篇文章很新，方法也独特，有很多可以借鉴和尝试的地方，希望给大家一点启示，有时间再好好整理)

    参考文献：Bloom Tree: A Search Tree Based on Bloom Filters for Multiple-Set Membership Testing, MyungKeun Yoon JinWoo Son Seon-Ho Shin, IEEE INFOCOM 2014