1.引言
bloomfilter过滤器,是一种利用极小错误换取极大空间节省的hash查询算法,它不适用于“零错误”的查询应用中。在谈到bloomfilter,先分析何为查询,查询的类别。
2.查询算法概述
- 查询算法概述
查询(Search)是数据处理最常见的一种运算。查询就是在数据集合中寻找满足
某种条件的数据对象。衡量一个查询算法的性能,需要在时间和空间方面进行权衡。对于不同方式存储结构所表示的集合,相应的查询方法也不相同。为了提高查询速度,往往采用某种特殊的组织方式来表示集合信息。 - 查询算法分类
1)地址转换的哈希查询算法(hashing)和树型结构查询算法(tree)
哈希查询算法由哈希存储表和哈希函数组成。元素的表示和查询是通过计算哈希函数获得相应的哈希地址,在哈希表上完成元素的插入和查询匹配操作。基于树型结构的查询算法在表示集合元素时采用分层树结构,信息存储到树中的结点。树型结构有多种组织方式(如二叉树、AVL 树、B 树等)。
2)内部查询算法(Internal)和外部查询算法(external)
按照信息存储和操作在计算机系统中的位置。内部查询算法将信息存储到计算机高速缓存和计算机主存中,外部查询算法将信息存储到计算机主存外的二级存储器。
3)静态查询算法(static)和动态查询算法(dynamic)
按照支持查询集合否可以动态变化
4)序列查询算法(digital)和非序列查询算法(non_digital)
序列查询算法又可以称为串匹配查询算法。串是由一系列连续的符号(字符)
组成。
5)单属性查询算法(actual)和多属性查询算法(attribute)
按照元素的属性值多少
6)精确查询算法(exact)和近似查询算法(approximate)
按照是否允许查询误判 - 哈希查询算法
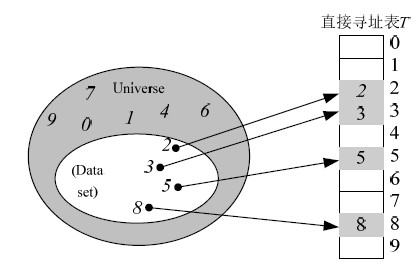
1)基于直接寻址表查询算法
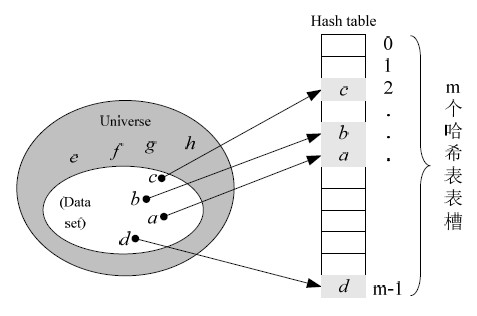
2)哈希查询算法
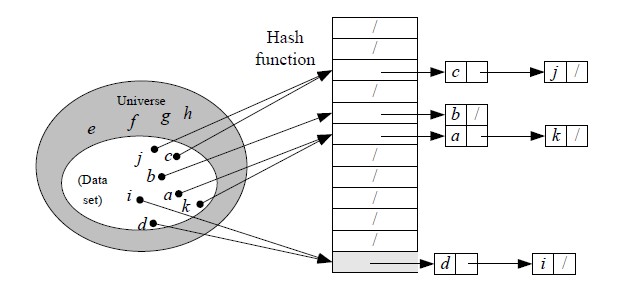
哈希查询算法中,一个哈希表槽里的每一个表槽可能对应对个查询元素,此时出现冲突,可以通过将表槽以链表的形式存储,但是如此有可能出现极端现象,某个表槽元素非常多,以至于hash查询算法退化为一般的查询算法(O(n)).
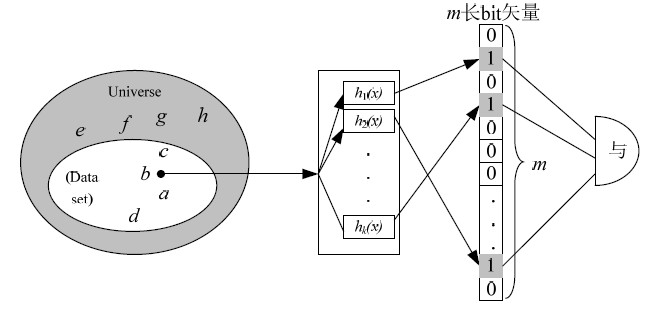
3)bloomfilter查询算法
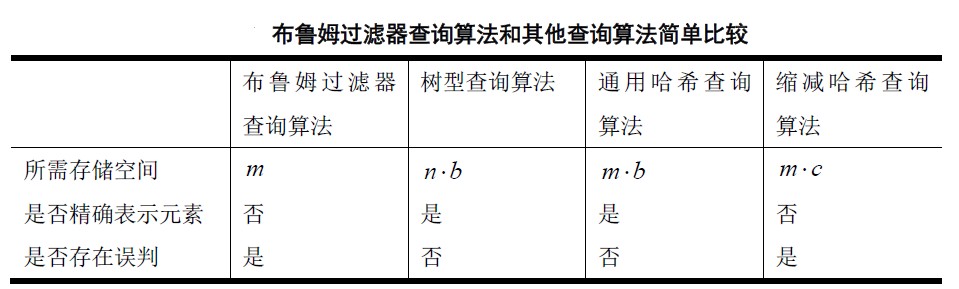
从通用哈希查询算法到缩减哈希查询算法,哈希表槽大小由b 位变为c 位,
虽然存在查询误差,但是可以节约空间1- c / b的存储空间。当哈希表槽退化为 1
位时,哈希表就退化为一个m 位长的位串,这时就演化为布鲁姆过滤器查询算法
查询算法比较:
1.存储空间 2.查询误判 3.查询判别过程 4.元素插入
3.BF查询算法
3.1标准布鲁姆过滤器查询算法
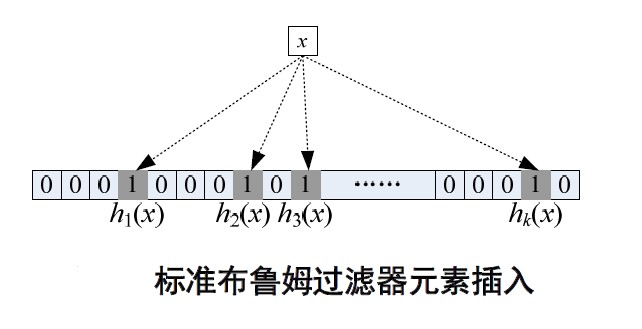
标准布鲁姆过滤器查询算法具体描述如下:数据集合{s1,s2,…,sn} 共有 n个元素通过k 个哈希函数h1,h2,…,hk映射到长度为m 位的向量V中。通常说布鲁
姆过滤器表示的汇总信息(summary)就是指这个向量V,用BF 表示。每一个哈希
函数相互独立且函数的取值范围为{0,1,2,…,m-1}。
3.2标准布鲁姆过滤器理论分析
用三元组{n,m, k}形式化表示一个标准布鲁姆过滤器,其中n:集合S 的元素个数;m:向量V 的长度;k:哈希函数个数。我们用p 表示向量V 中一位为0 的概率,则1-p 为1 的概率。同时,在本文的讨论中,假设哈希函数取值服从均匀分布,当集合中所有元素都映射完毕后,V 向量任一位为0 的概率:
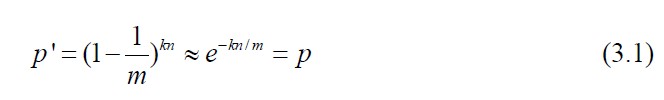
当不属于集合的元素误判断属于集合时,元素在V 向量的对应位置都必须为
1。即元素的误判率应为
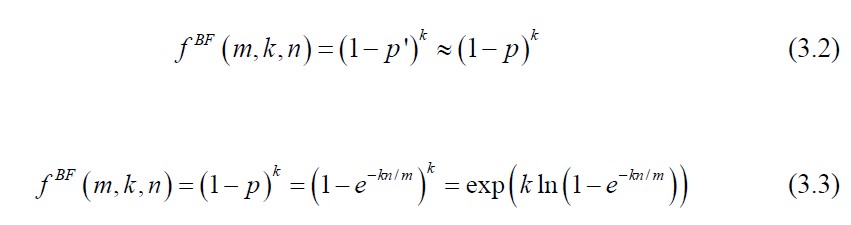
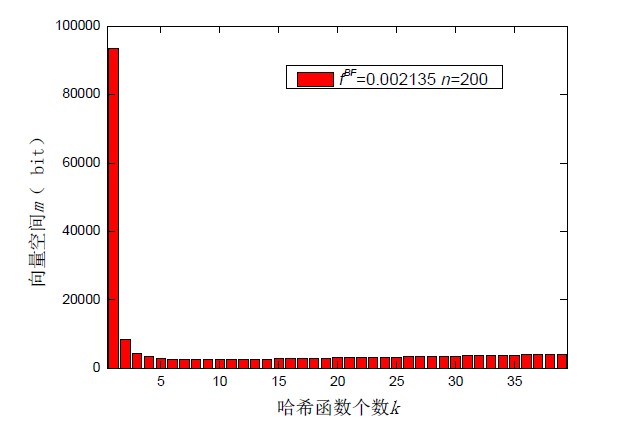
当集合元素个数n 和向量空间m 一定时,如何选择合适的哈希函数个数k 使得布鲁姆过滤器误判率f 最小
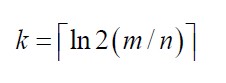
4.适用范围
可以用来实现数据字典,进行数据的判重,或者集合求交集
5.拓展
标准的BF是不支持删除操作,Counting bloom filter(CBF)将位数组中的每一位扩展为一个counter,从而支持了元素的删除操作。标准的BF是不可逆的,即由value是无法得到key,Invertible Bloom Lookup Tables实现了BF的逆向求值操作。
参考文献:
1.布鲁姆过滤器查询算法及其应用研究(谢鲲)
2.http://blog.csdn.net/v_july_v/article/details/6685894






















 434
434

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








