高斯消元法模版题,但套模版没用。。
先回顾一下线性代数的知识。
若要求解如下方程:
首先,其系数矩阵为
然后,其增广矩阵为:
然后若要求解这个方程,首先将第一行第一个元素化为1,即:第一行乘以1/3。
然后将第二、三行减去第一行五倍:
扯淡了不是。。太麻烦了。。。额,我不会告诉你我用matlab做的。。
a = [3,2,4; 5, 3, 1; 10, 2,2];
b = [10;1;3];
x = inv(a) * b;
x = a\b;
然后这个方程的解是-0.2059 -0.2500 2.7794。。。
好了废话少说。
题目是要求建立一个方程组:
(mat[1][1]*x[1] + mat[1][2]*x[2] + … + mat[1][n]*x[n])%7 =mat[1][n+1]
(mat[2][1]*x[1] + mat[2][2]*x[2] + … + mat[2][n]*x[n])%7 =mat[2][n+1]
…
…
(mat[m][1]*x[1] + mat[m][2]*x[2] + … + mat[m][n]*x[n])%7 =mat[m][n+1]
如果有解输出解得个数,如果无解Inconsistent data.无穷多组解Multiple solutions.
扯一句,什么时候无解?
系数矩阵的秩 不等于 增广矩阵的秩 时。反映在程序上就是:
for (i = row; i < N; i++)
{
if (a[i][M] != 0)
{
printf("Inconsistent data.\n");
}
}
什么时候无穷多解?
当增广矩阵的秩小于行列式的行数的时候。 反映在程序上就是:
if (row < M)
{
printf("Multiple solutions.\n");
}
好了,程序如下:
|
#include<iostream> #include<cstdio> #include<string.h> using namespace std; #define MOD 7 int a[310][310]; int N, M; char str1[5], str2[5]; int ans[310]; int solved(char s []) { if (s[0] == 'M') return 1; if (s[0] == 'T' && s[1] == 'U') return 2; if (s[0] == 'W') return 3; if (s[0] == 'T' && s[1] == 'H') return 4; if (s[0] == 'F') return 5; if (s[0] == 'S' && s[1] == 'A') return 6; if (s[0] == 'S' && s[1] == 'U') return 7; } int extend_gcd(int A, int B, int &x, int &y) { if (B == 0) { x = 1, y = 0; return A; } else { int r = extend_gcd(B, A%B, x, y); int t = x; x = y; y = t - A / B*y; return r; } } int lcm(int A, int B) { int x = 0, y = 0; return A*B / extend_gcd(A, B, x, y); } void Guass() { int i, j, row, col; for (row = 0, col = 0; row < N && col < M; row++, col++) { for (i = row; i < N; i++) if (a[i][col]) break; if (i == N) { row--; continue; } if (i != row) for (j = 0; j <= M; j++) swap(a[row][j], a[i][j]); for (i = row + 1; i < N; i++) { if (a[i][col]) { int LCM = lcm(a[row][col], a[i][col]);//利用最小公倍数去化上三角 int ch1 = LCM / a[row][col], ch2 = LCM / a[i][col]; for (j = col; j <= M; j++) a[i][j] = ((a[i][j] * ch2 - a[row][j] * ch1)%MOD + MOD)%MOD; } } } for (i = row; i < N; i++)//无解 { if (a[i][M] != 0) { printf("Inconsistent data.\n"); return; } } if (row < M)//无穷多解 { printf("Multiple solutions.\n"); return; } //唯一解时 for (i = M - 1; i >= 0; i--) { int ch = 0; for (j = i + 1; j < M; j++) { ch = (ch + ans[j] * a[i][j] % MOD)%MOD; } int last = ((a[i][M] - ch)%MOD + MOD)%MOD; int x = 0, y = 0; int d = extend_gcd(a[i][i], MOD, x, y); x %= MOD; if (x < 0) x += MOD; ans[i] = last*x / d%MOD; if (ans[i] < 3) ans[i] += 7; } for (int i = 0; i < M; i++) { if (i == 0) printf("%d", ans[i]); else printf(" %d", ans[i]); } printf("\n"); } int main() { while (scanf("%d%d", &M, &N), N || M) { memset(a, 0, sizeof(a)); memset(ans, 0, sizeof(ans)); int K; for (int i = 0; i < N; i++) { scanf("%d%s%s", &K, str1, str2); int last = ((solved(str2) - solved(str1) + 1)%MOD + MOD)%MOD; for (int j = 0; j < K; j++) { int v; scanf("%d", &v); a[i][v - 1] = (a[i][v - 1] + 1)%MOD; } a[i][M] = last; } Guass(); } } |








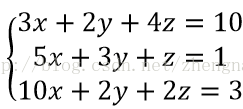
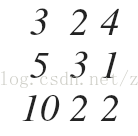
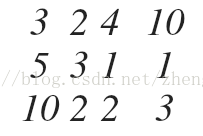
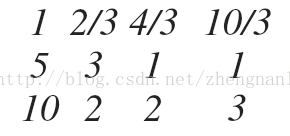
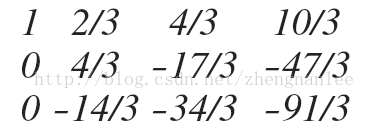
















 2326
2326

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








