为什么计算机进行小数运算时会出错

计算机进行小数运算出错的原因

计算机之所以会出现运算错误，是因为“有一些十进制数的小数无法转换成二进制数”。

例如，十进制数0.1，就无法用二进制数正确表示，小数点后面即使有几百位也无法表示。

因为无法正确表示的数值，最后都变成了近似值。计算机这个功能有限的机器设备，是无法处理无限循环的小数的。

因此，在遇到循环小数时，计算机就会根据变量数据类型所对应的长度将数值从中间截断或者四舍五入。我们知道，将0.3333…这样的循环小数从中间截断会变成0.333333，这时它的3倍是无法得出1 的（结果是0.999999），计算机运算出错的原因也是同样的道理。

浮点数

很多编程语言中都提供了两种表示小数的数据类型，分别是双精度浮点数和单精度浮点数。 双精度浮点数类型用64 位、 单精度浮点数类型用32 位来表示全体小数。

浮点数是指用符号、尾数、基数和指数这四部分来表示的小数。因为计算机内部使用的是二进制数，所以基数自然就是2。因此，实际的数据中往往不考虑基数，只用符号、尾数、指数这三部分即可表示浮点数。也就是说，64 位（双精度浮点数）和32 位（单精度浮点数）的数据，会被分为三部分来使用。

浮点数的表现方式有很多种，这里我们使用最为普遍的IEEEA 标准。
（IEEE（Institute of Electrical and Electronics Engineers）是指美国电气和电子工程师协会。该协会制定了计算机领域的各种规定。读作“eye-triple-e，I-3E”）

双精度浮点数和单精度浮点数在表示同一个数值时使用的位数不同。此外，双精度浮点数能够表示的数值范围要大于单精度浮点数。

整数是指使用包含表示符号的最高位在内的全体来表示的一个数值。而浮点数是由符号部分、尾数部分和指数部分这三部分独立的数值组合而成的。

符号部分是指使用一个数据位来表示数值的符号。该数据位是1时表示负，为0 时则表示“正或者0”。这和用二进制数来表示整数时的符号位是同样的。数值的大小用尾数部分和指数部分来表示。例如，小数就是用“尾数部分× 2 的指数部分次幂”这样的形式来表示的。

而尾数部分和指数部分并不只是单单存储着用整数表示的二进制数。 尾数部分用的是“将小数点前面的值固定为1 的正则表达式”，而指数部分用的则是“EXCESS 系统表现”。

正则表达式和EXCESS 系统

按照特定的规则来表示数据的形式即为正则表达式。

尾数部分使用正则表达式

尾数部分使用正则表达式 ，可以将表现形式多样的浮点数统一为
一种表现形式。例如，十进制数0.75 就有很多种表现形式。

虽然它们表示的都是同一个数值，但因为表现方法太多，计算机在处理时会比较麻烦。因此，为了方便计算机处理，需要制定一个统一的规则。

例如，十进制数的浮点数应该遵循“小数点前面是0，小数点后面第1 位不能是0”这样的规则。根据这个规则，0.75 就是“0.75×10 的0 次幂”，也就是说，只能用尾数部分是0.75、指数部分是0 这个方法来表示。

在二进制数中，我们使用的是“ 将小数点前面的值固定为1 的正则表达
式”。

根据这个规则来表示小数的方式，就是正则表达式。
除小数之外，字符串以及数据库等，也都有各自的正则表达式。

指数部分使用EXCESS 系统

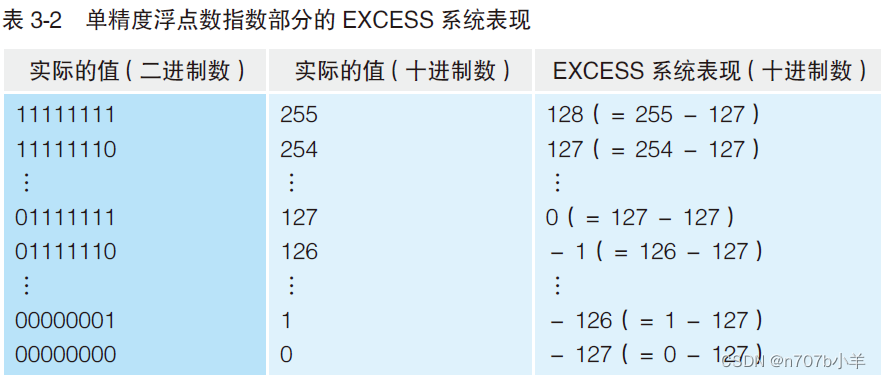
接下来，让我们一起来看一下指数部分中使用的EXCESS 系统，使用这种方法主要是为了表示负数时不使用符号位。在某些情况下，在指数部分，需要通过“负n次幂”的形式来表示负数。 EXCESS系统表现是指，通过将指数部分表示范围的中间值设为0，使得负数不需要用符号来表示。

EXCESS 系统可能不太好理解，下面举例来说明。假设有这样一个游戏，用１～13（A～K）的扑克牌来表示负数。这时，我们可以把中间的7 这张牌当成0。如果扑克牌7 是0，10 就表示＋3，3 就表
示－4。事实上，这个规则说的就是EXCESS 系统。

如何避免计算机计算出错

计算机计算出错的原因之一是，采用浮点数来处理小数（另外，也
有因“位溢出”而造成计算错误的情况）。作为程序的数据类型，不管是使用单精度浮点数还是双精度浮点数，都存在计算出错的可能性。

接下来将介绍两种避免该问题的方法：

首先是回避策略，即无视这些错误。
根据程序目的的不同，有时一些微小的偏差并不会造成什么问题。例如，假设使用计算机设计工业制品。将100 个长0.1 毫米的零件连接起来后，其长度并非一定要是10 毫米，10.000002 毫米也没有任何问题。一般来讲，在科学技术计算领域，计算机的计算结果只要能得到近似值就足够了。那些微小的误差完全可以忽略掉。

另一个策略是把小数转换成整数来计算。
计算机在进行小数计算时可能会出错，但进行整数计算（只要不超过可处理的数值范围）时一定不会出现问题。因此，进行小数的计算时可以暂时使用整数，然后再把计算结果用小数表示出来即可。例如，本章一开头讲过的将0.1 相加100 次这一计算，就可以转换为将0.1 扩大10 倍后再将1 相加100次的计算，最后把结果除以10 就可以了。