题目:有一分数序列:2/1,3/2,5/3,8/5,13/8,21/13…求出这个数列的前20项之和。
import javax.swing.JOptionPane;
public class CalSum {
//分数序列:2/1,3/2,5/3,8/5,13/8,21/13...
public static void main(String[] args) {
JOptionPane.showMessageDialog(null, calSum(20));
}
static String calSum(int n) {
double sum = 0;
for (int i=1; i<=n; i++) {
sum += getNum(i);
}
return String.format("%.5f", sum);
}
static double getNum(int n) {
return getSequence(n+1)/(double)getSequence(n);
}
static int getSequence(int n) {
if (n == 1) return 1;
if (n == 2) return 2;
return getSequence(n-1)+getSequence(n-2);
}
}







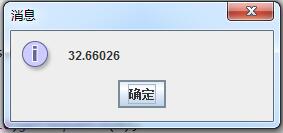














 3600
3600

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








