一元积分学概念与性质-CSDN博客

当遇到一些比较复杂的具体的函数，而且区间内存在振荡间断点的函数 $f(x)$ 时，通过先求出他的原函数 $F(x)$ ，然后通过求导 $F(x)$ ，若得出是 $f(x)$ ，且在一些需要处理的点处，仍然可以得出 $F'(x_{0}) = f(x_{0})$ ,那么 $F(x)$ 就是 $f(x)$ 的原函数，也就是说存在不定积分
$F'(x) = f(x)$ 得出，若 $f(x)$ 处处有定义，则 $F(x)$ 处处可导 $\Rightarrow$ $F(x)$ 处处连续
$F'(x) = f(x)$ 得出，若 $F(x)$ 处处可导，且 $F(x)$ 的导数值刚刚好等于 $f(x)$ 函数值，则 $f(x)$ 处处有定义

(1)连续函数 $f(x)$ 必有原函数 $F(x)$ 。

(2)含第一类间断点和无穷间断点的函数 $f(x)$ 在包含该间断点的区间内必没有原函数 $F(x)$ ，但若 $f(x)$ 在包含振荡间断点区间内不确定是否有原函数 $F(x)$ 。

下面时对第一条定理的证明：

注：一旦 $f(x)$ 连续就会有下面的式子成立：

1. $\int f(x)dx = \int_{a}^{x}f(t)dt +C$ 这个式子是不定积分与定积分的一个桥梁，但是实际上不定积分与定积分没有任何关系

2. $[\int_{a}^{x}f(t)dt]' = f(x)$ 即不定积分的导数就是 $f(x)$ 。

对于第二条定理的证明：

通过研究 $f(x)$ 具备什么性质，从而推断第二条定理中第一类间断点的函数 $f(x)$ 在包含该间断点的区间内必没有原函数 $F(x)$ 正确性

、上面的b的结论在几何上说明了在 $x_{0}$ 点处，说明在 $x_{0}$ 处附近点的斜率就是在 $x_{0}$ 处导函数值

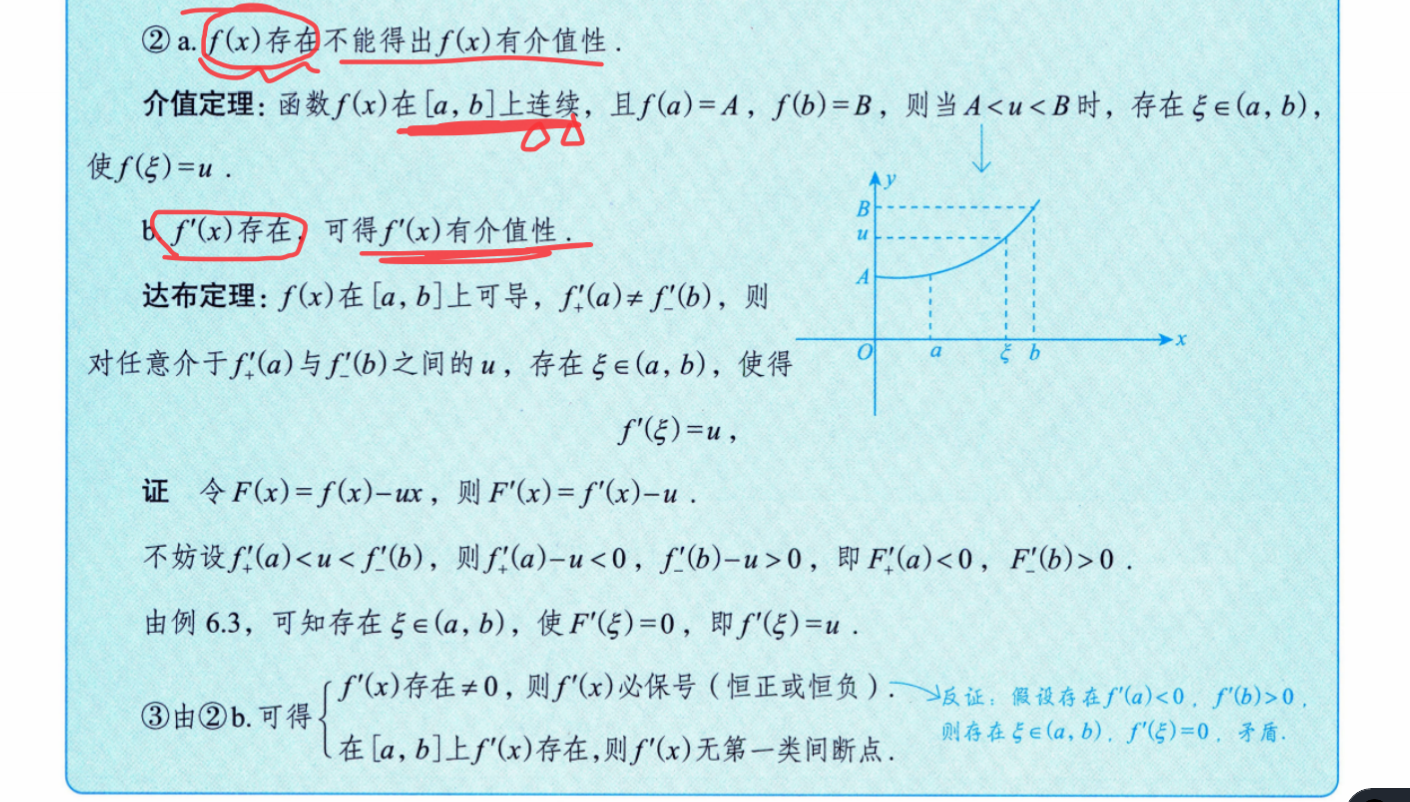
上面的介值性比较宽泛的定义：介值性是一个更弱的全局性质。它只要求函数在某个区间内“覆盖”所有中间值，而不要求函数在每个点都连续。因此，连续性足以保证介值性，但介值性不需要连续性。

而如果导数存在的话，那么根据导数定义和洛必达法则可以得出在 $x_{0}$ 处附近的点 $x$ 的极限也是导数 $f'(x_{0})$ 的值，说明这其中是没有突变，而是平滑度过，所以肯定会有介值性。

也就是说首先：导数不能有“跳跃”间断，因为根据导数的定义，如果导数在某点存在，它必须满足某种“平滑”过渡。因此，即使导数不连续，它仍然必须通过所有中间值。

另一个角度证明第一类间断点的以及无穷间断点函数 $f(x)$ 在包含该间断点的区间内必没有原函数 $F(x)$ 正确性

证明振荡间断点函数 $f(x)$ 在包含该间断点的区间内不确定原函数 $F(x)$ 正确性

由上面的例子说明：对于某些振荡间断点来说，其实是将在无穷区间内的无穷延伸，但是振荡间断点则是在有限区间内进行无穷延伸。

上面的第四，可以详细写成：

若函数 $f(x)$ 在某个区间上可导，则其导函数 $f'(x)$ 满足介值性（达布性质）。此时：

$f'(x)$ 可能连续（例如 f(x)=x2f(x)=x2，其导函数 f′(x)=2xf′(x)=2x 连续）。
$f'(x)$ 也可能不连续，但此时的不连续只能是振荡型间断点（例如 f(x)=x2sin⁡(1/x)f(x)=x2sin(1/x) 在 x=0x=0 附近，其导函数在 x=0x=0 处振荡无极限）。
$f'(x)$ 不能有跳跃间断点（即左右导数存在但不相等的情况），因为这会违反介值性。

简化为步骤：

几何意义

定积分的精确定义

必要性：定积分的存在性，也称一元函数的常义可积性，即“区间有限，函数有界”。

充分性：

定理：设 $f(x)$ 是 $[a,b]$ 上的非负连续函数，那么只要 $f(x)$ 不恒等于0，则必有：

$\int_{a}^{b}f(x)dx >0$

推广为：设 $f(x)$ ， $g(x)$ 是 $[a,b]$ 上的非负连续函数,且 $f(x)-g(x)\geqslant 0$ ,且不恒等于0则必有：

$\int_{a}^{b}f(x)dx-\int_{a}^{b}g(x)dx >0$

两个重要结论

上面的两个重要结论要结合等价无穷小替换进行使用

对于无穷区间的反常积分，即 $\int_{a}^{+\infty }f(x)dx$ ，关键是看 $f(x)\rightarrow 0$ 的速度(即无穷小的阶数)
对于有限区间的无界函数，即 $\int_{a}^{b}f(x)dx$ ，其中 $\lim_{x \to a^{+}}f(x) = \infty$ 或者是 $\lim_{x \to b^{-}}f(x) = \infty$ ,关键是 $f(x)\rightarrow \infty$ 的速度(无穷大的阶数)
关键是在比较时，如何找到恰当的比较对象。