算法：臭皮匠排序

在《算法导论》第二版第 7 章（快速排序）的思考题（第 95 页）中提及到一种 低效的递归排序算法：Stooge 排序， Howard、Fine 等教授将这个算法称为 漂亮排序算法（完美排序算法）。

经过证明，Stooge 排序的性能是慢于冒泡排序的，因为这个，在《算法导论》中作者悄悄的 “diss” 了一下这几位终生教授，“怀疑”他们是否“名副其实”。

顾名思义， 漂亮排序算法 它的代码实现 看、上、去 很整齐很好看！

private static void stoogeSort(int[] A, int low, int high){
    if(A[low] > A[high]) swap(A, low, high);
    if(low + 1 >= high ) return;
    int split = (high - low + 1) / 3;
    stoogeSort(A, low, high - split);
    stoogeSort(A, low + split, high);
    stoogeSort(A, low, high - split);
}

golang版本

package main

import (
	"fmt"
)

func inner_stoogeSort( arr[]int,  low int,  high int)[]int{
	if(arr[low] > arr[high]){
		arr[low], arr[high] = arr[high], arr[low]
	}

	if(low + 1 >= high){
		return arr
	}

	part := (high - low + 1)/ 3;
	inner_stoogeSort(arr, low, high - part) //
	inner_stoogeSort(arr, low + part, high)
	inner_stoogeSort(arr, low, high - part)
	return arr;
}

func StoogeSort( arr[]int)[]int{
	length := len(arr)
	if length  <= 1{
		return arr
	}else{
		return inner_stoogeSort(arr, 0, length - 1);
	}
}

func main() {
	arr:=[]int {9, 1, 3, 6, 5, 4, 2, 7, 8}
	fmt.Println(StoogeSort(arr))
	fmt.Println(arr)
}

• 如果最后一个值小于第一个值，则交换这两个数
• 如果当前集合元素数量大于等于3：
  • 使用臭皮匠排序前2/3的元素
  • 使用臭皮匠排序后2/3的元素
  • 再次使用臭皮匠排序前2/3的元素
    
    代码整体的思路就是基于递归来实现的，具体操作就是：对于传入的数组先将头部与尾部进行排序，然后递归调用排序前三分之二，再递归调用排序后三分之二，最后再递归调用排序前三分之二

1、对传入的数组的头尾元素进行比较 【low = 0， high = 8】

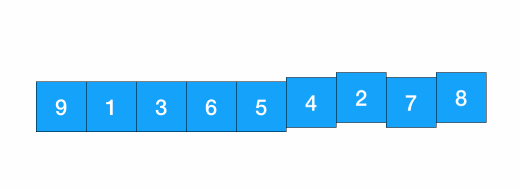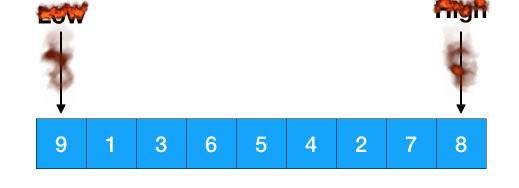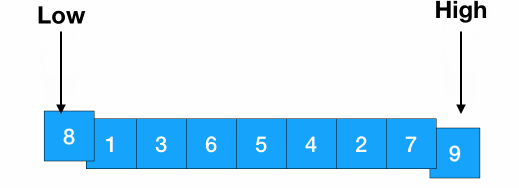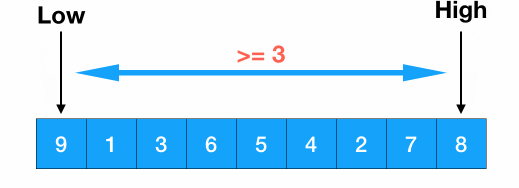
将数组三等分： split = [8 - 0 + 1] / 3 = 3

2、同样的逻辑递归的排序数组的前 2 / 3 区域 【0， 8 - 3 】= [0, 5]


splid = (5 - 0 + 1) / 3 = 6 / 3 = 2

• 同样的逻辑递归的排序数组的前 2 / 3 区域 [0, 5 - 2] = [0, 3]
  
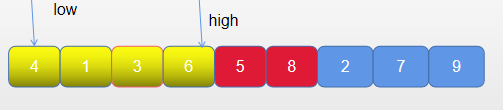
  此时4、6无需交换
  数据3分：splid = (3 - 0 + 1)/3 = 1
  

• 同样的逻辑递归的排序数组的前 2 / 3 区域[0, 3 - 1] = [0, 2]
  
  splid = (2 - 0 + 1) / 3 = 1
  

3、同样的逻辑递归的排序数组的后 2 / 3 区域[0 + 1, 2] = [1, 2]， splid = 1

3、同样的逻辑递归的排序数组的前 2 / 3 区域[0 , 2 - 1] = [0, 1]，

可以看出前3个以及有序了

4、 回到第2个递归, 逻辑递归的排序数组的后 2 / 3 区域[0+2, 5] = [2, 5]， sp = 2

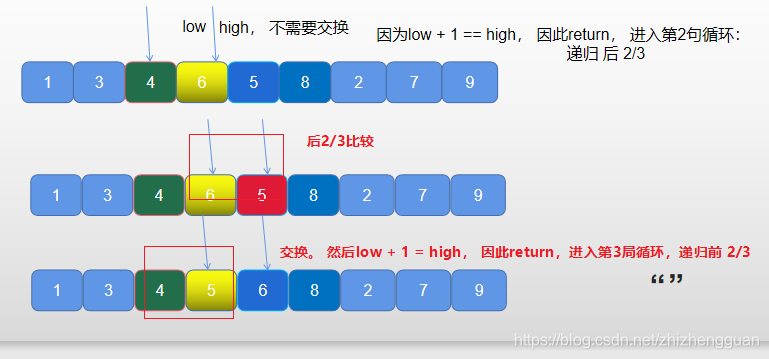
第3局循环已经完成， 可以看到 4，5，6 局部有序，出栈。

5、回到第3个递归：递归前 2/3 .。。。。

排序完成！

这个算法的复杂度为 T(n) = 3 T( 2n / 3 ) + 1，已被其它大牛证明时间复杂度接近于 O(n2.71) ，对比于一般的排序算法，比如冒泡、选择等常见的 O(n2) 排序算法，排序过程上慢很多。

所以，它除了好看，目前也没发现有啥用：一顿操作瞎装逼，一看性能二点七！

再补充一个有趣的点，这个算法也被称之为 臭皮匠算法： 三个臭皮匠顶个诸葛亮（在代码实现中涉及到三等分这个概念）。