升余弦滤波器的频域响应

升余弦滤波器又叫RC滤波器，其传输函数H（ω）如下[1]：

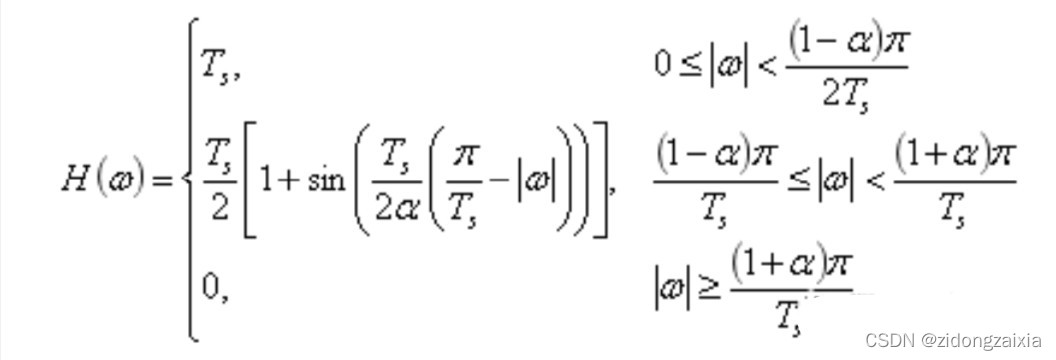
其中α为滚降因子，Ts为采样时间，不同滚降因子对应的传输特性图如下所示：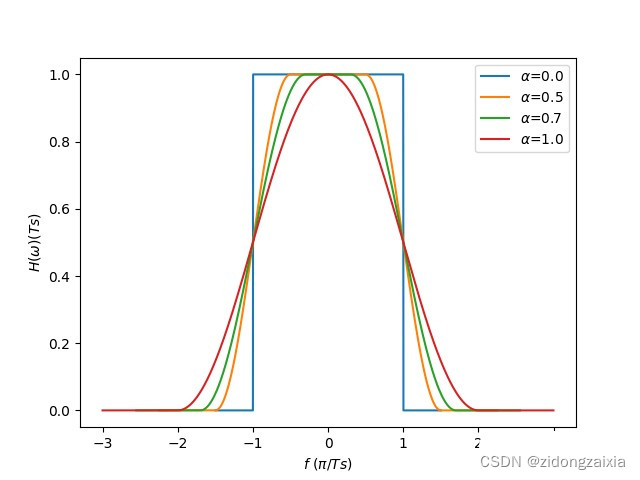

由以上波形可以看出，滚降因子α越大，则信号带宽就会越宽；反之，则信号带宽就越窄。以下为使用python代码编写的RC滤波器频域响应代码：

import numpy as np
import matplotlib.pyplot as plt
def hwRrc(Ts = 1, alpha = 0.2, i=0):
    # hw(w + 2*pi*i/Ts)
    if Ts==0:
        Ts = 1
    endw = (1+alpha) * np.pi /Ts *1.5
    w0 = np.arange(-endw, endw, 0.01)
    w