回溯算法-01遍历所有排列方式问题

遍历所有排列方式

• 前言
  • 回溯采用试错的方法解决问题，一旦发现当前步骤失败，回溯算法就返回上一个步骤，继续另一种方案继续试错。
  • 回溯算法的优点是速度快，没有尝试所有路径就可能找到答案。当然，如果运气不好，回溯算法就是一个暴力遍历（当答案就是最后一条搜索路径）。
  • 回溯算法又称为试探法，它的主要思想如上。回溯算法针对大多数问题有如下特点：问题的答案有多个元素、答案需要满足一些约束（如数独）、寻找答案的方式每个步骤相同。回溯算法逐渐构建答案，并在确定候选元素不满足约束后立即放弃候选元素，知道找到答案的所有元素。
• 简介
  • 全排列一般答案为n!种方案，但是当想知道所有的排列方式的时候，DP等算法就不是那么合适了。此时回溯将是不错的选择。
• 问题描述
  • 有四本书A，B，C，D，一次只能从图书馆借一本，试问有多少种借书方式？
• 问题分析
  • 这个问题很简单，不妨认为有4个空位，第一个位置选择了A，那么第二个位置剩下三种选择，假设第二个位置选择了B，第三个位置剩下两种选择，以此类推。显然，单纯写这个代码是个四层循环，这样写不仅编码困难，对其他问题还要重新编码并且必须要知道输入数组的长度，这不是想要的解法。
  • 其实再看看这个循环，它们都很类似。
    • 选择第一本书有4中选择，答案就是这四种选择各结尾增加剩下的三本书的排列情况，那么只需要知道剩余三本书的排列集合就行了。
    • 排列剩下的三本书的时候，对第一本有三种选择，只需要知道剩下两种排列情况即可。
    • 最后，排两本书的时候，只需要知道最后一本是什么就行了。
  • 其实就是一个大问题套着小问题，问题都是一个问题，参数有所不同罢了，问题是一样的：输出排序集合。
  • 带修改参数递归很适合实现这样的问题。
• 代码

  •   # -*-coding:utf-8-*-
      
      result = []
      
      
      def solve(array, solution):
          global result
          if len(array) == 0:
              # 表示所有书都分配完毕，输出答案
              result.append(solution)
              return
          for i in range(len(array)):
              new_solution = solution + [array[i]]
              new_array = array[:i] + array[i+1:]
              solve(new_array, new_solution)
      
      
      if __name__ == '__main__':
          input = ['A', 'B', 'C', 'D']
          solve(input, [])
          for item in result:
              print(item)
          print("共{}种排列".format(len(result)))
    

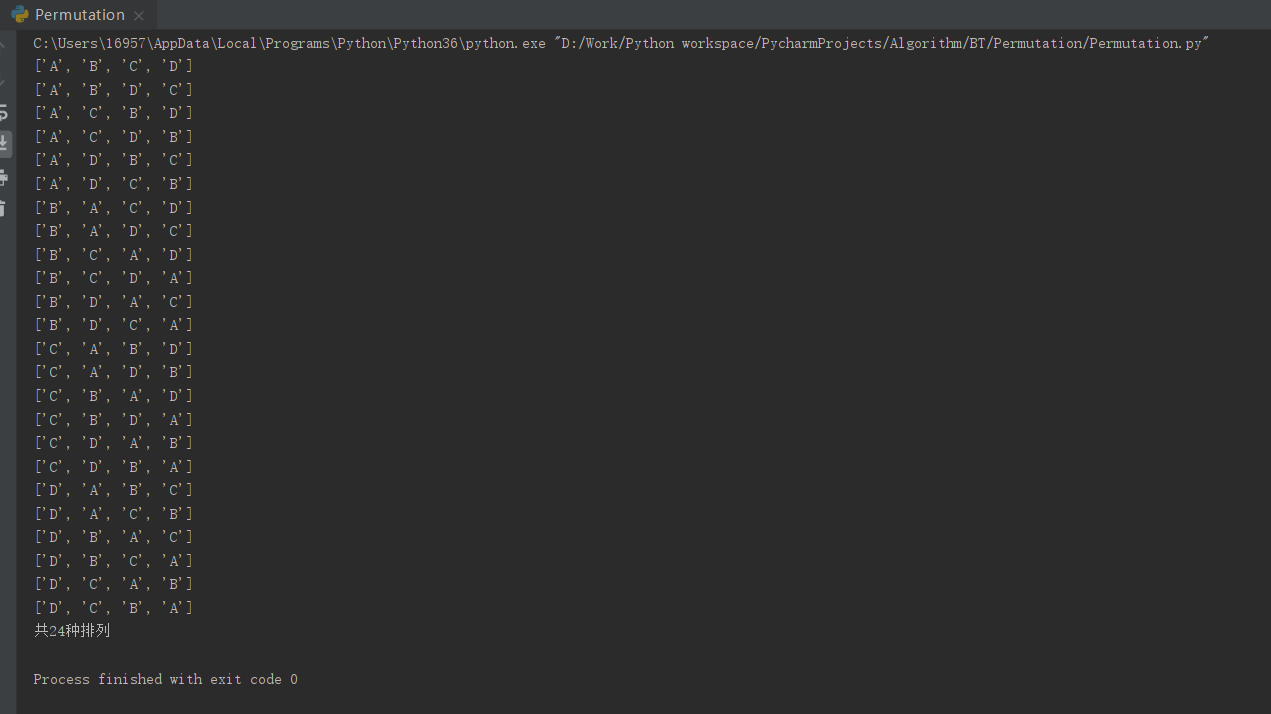
• 运行结果
  • 
• 补充说明
  • 具体代码可以查看我的Github，欢迎Star或者Fork
  • 参考书《你也能看得懂的Python算法书》
  • 书中错误已经修改