稀疏矩阵(Sparse Matrix):对于那些零元素数目远多于非零元素数目,且非零元素分布没规律的矩阵。
通过三元组线性表创建稀疏矩阵,并对其进行矩阵转置操作
/*
* 稀疏矩阵(三元组)
* CreatedOn: 2015-11-12
* CreatedBy: Jackie Lee(天宇遊龍)
*/
#include <stdio.h>
#include <stdlib.h>
typedef struct tuple
{
int row; // 行号
int col; // 列号
int value; // 元素值
}Tuple, *PTuple;
typedef struct spmatrix
{
int maxNum; // 最多元素数
int rows; // 行数
int cols; // 列数
int num; // 非零元素实际个数
Tuple *data; // 存储非零元素的值及一个表示矩阵行数、列数总的非零元素数目的特殊三元组
}SparseMatrix, *PSparseMatrix;
/*
0 2 0 5
0 0 3 0
6 0 0 0
0 7 0 0
0 0 0 8
*/
void CreateSMatrix(PSparseMatrix psm);
void SetData(PSparseMatrix psm, int index, int row, int col, int value);
SparseMatrix* Transpose(PSparseMatrix psm);
void Print(PSparseMatrix psm);
int main(void)
{
SparseMatrix sm, *psm;
CreateSMatrix(&sm); // 定义
printf("Original Sparse Matrix\n");
Print(&sm);
psm = Transpose(&sm);
printf("the Sparse Matrix after Transpose\n");
Print(psm);
// 释放
free(sm.data);
// 释放转置矩阵
free(psm->data);
free(psm);
return 0;
}
// 创建稀疏矩阵
void CreateSMatrix(PSparseMatrix psm)
{
psm->maxNum = 5 * 4; // 5 x 4矩阵
psm->cols = 4; // 列
psm->rows = 5; // 行
psm->num = 6; // 6个非零元素
psm->data = (Tuple *)malloc(sizeof(Tuple) * psm->num);
SetData(psm, 0, 0, 1,2); // 0行1列值为2
SetData(psm, 1, 0, 3,5); // 0行3列值为5
SetData(psm, 2, 1, 2,3); // 1行2列值为3
SetData(psm, 3, 2, 0,6); // 2行0列值为6
SetData(psm, 4, 3, 1,7); // 3行1列值为7
SetData(psm, 5, 4, 3,8); // 4行3列值为8
}
void Print(PSparseMatrix psm)
{
int i,r,c,v;
//Tuple *pdata = (Tuple *)malloc(sizeof(Tuple) * psm->maxNum); // 创建矩阵真实的大小
int **pdata = NULL;
pdata = (int **)malloc(sizeof(int *) * psm->rows); // 创建行//(int **)malloc(sizeof(int) * psm->rows * psm->cols);
for (i = 0; i < psm->rows; ++i) // 创建列
{
pdata[i] = (int *)malloc(sizeof(int) * psm->cols);
memset(pdata[i], 0, sizeof(int) * psm->cols);
}
for (i = 0; i < psm->num; ++i) // 稀疏矩阵中非零元素
{
r = psm->data[i].row;
c = psm->data[i].col;
v = psm->data[i].value;
pdata[r][c] = v;
}
printf("*********************print the Sparse Matrix*********************\n");
for (r = 0; r < psm->rows; ++r)
{
for (c = 0; c < psm->cols; ++c)
{
printf("%4d", pdata[r][c]);
}
printf("\n");
}
for (i = 0; i < psm->rows; ++i)
{
free(*(pdata + i));
pdata[i] = NULL;
}
free(pdata);
}
// 设置三元矩阵元素值
// 索引,行,列,值
void SetData(PSparseMatrix psm, int index, int row, int col, int value)
{
psm->data[index].col = col;
psm->data[index].row = row;
psm->data[index].value = value;
}
// 转置
SparseMatrix* Transpose(PSparseMatrix psm)
{
int p, q, col;
SparseMatrix *sm = (SparseMatrix*)malloc(sizeof(SparseMatrix));
sm->cols = psm->rows;
sm->rows = psm->cols;
sm->num = psm->num;
sm->data = (Tuple *)malloc(sizeof(Tuple) * sm->num);
if(sm->num > 0)
{
q = 0; // 控制转置矩阵下标
for (col = 0; col < psm->cols; ++col) // 扫描矩阵列
{
for (p = 0; p < psm->num; ++p) // p控制被转置矩阵下标
{
if(psm->data[p].col == col)
{
sm->data[q].row = psm->data[p].col;
sm->data[q].col = psm->data[p].row;
sm->data[q].value = psm->data[p].value;
q++;
}
}
}
}
return sm;
}效果:








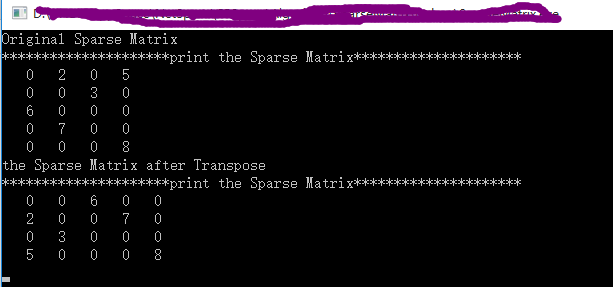














 128
128

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








