算法导论 第12章 二叉查找树

二叉查找树的概念和性质

       二叉查找树（Binary Search Tree）是这样的一棵树：设节点x的左右孩子分别为y,z，那么key[x] <= key[z]且key[x] >= key[x]，而它的以y和z分别为根的左右子树也是满足这样条件的二叉树。

       二叉查找树支持多种动态集合操作，包括locate，minimum，maximum，predecessor，successor，insert以及erase等操作，既可以作为字典，也可以作为优先级队列。

       二叉查找树上执行的基本操作的时间和树的高度成正比。对于一颗含有n个节点的完全二叉树，其高度为O(lgn)，故这些操作的最坏运行时间为O(lgn)。但是，如果输入不均，那么二叉树有可能退化为线性链，那么此时的操作最坏运行时间就为O(n)了。

二叉树的结构

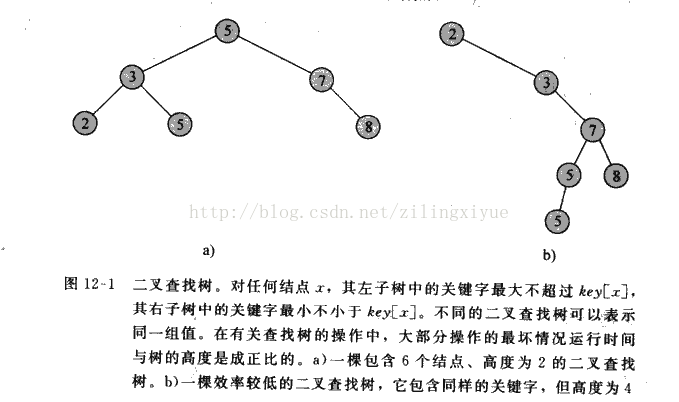
        一棵二叉查找树是按二叉树结构来组织的，这样就可以用链表结构来表示，其中的每一个节点都是一个对象。节点中除了key域和一些卫星数据之外，还包含left,right和parent指针域，它们分别指向该节点的左节点，右节点和父节点。如果其中的某个指针域不存在，则将其标为NULL。根节点是唯一一个不存在父节点的节点。下图是两棵二叉查找树：

二叉查找树的操作

       1、遍历

       二叉树的定义是递归的，根据这一性质，可以用一个递归的算法输出二叉树中的所有关键字，根据某节点相对于其左右节点的输出顺序可以分为先根遍历、中根遍历以及后根遍历，其中中根遍历的关键字输出时从到大排序的。下面给出的是中根遍历的算法：

inTraversal(x)
{
	if (x != NULL)
	{
		inTraversal(left[x]);
		print(key[x]);
		inTraversal(right[x]);
	}
}

显然，时间复杂度为O(n)。

       2、查找

       给定指向树根的指针和一个关键字，下列算法将返回指向该关键字的指针，如果不存在，则返回NULL。

locate(x, k)
{
	if (x == NULL) or key[x] == k
		return x;
	if (k <= key[x])
		return locate(left[x], k);
	else
		return locate(right[x], k);
}

      3、最大和最小关键字

      要查找二叉树中的最小关键字，只需从根节点开始一直沿着各节点的left域往左，直到遇到NULL为止。要查找最大关键字，过程与前者对称。下面是查找最小关键字的递归算法：

minimum(x)
{
	if (left[x] == NULL)
		return key[x];
	return minimum(left[x]);
}

      4、前驱和后继

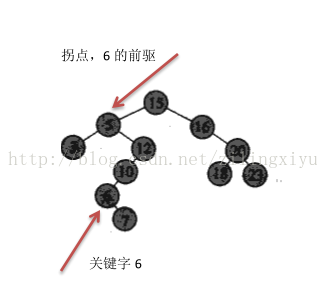
       给定一个节点x，其前驱（后继）指的是按中序遍历的输出顺序中该节点的前一个关键字（后一个关键字）。如果树中各节点的关键字均不相同，则x的前驱（后继）是比key[x]小（大）的关键字里面最大（小）的。再结合二叉查找树的性质，无需比较我们就可以找到节点x的前驱（后继），即，如果x的左（右）子树不空，则其前驱（后继）是左（右）子树中的最大（小）关键字；否则，其前驱（后继）就在沿着左（右）指针一直向上遇到的第一个拐点处，如下图关键字6的前驱：

下面是寻找前驱的算法：

predecessor(x)
{
	if (left[x] != NULL)
		return maximum(left[x]);
	y <- parent[x];
	while (y != NULL && x != left[y])
	{
		x <- y;
		y <- parent[y];
	}
	return y;
}

      5、插入和删除

       插入和删除操作会引起二叉查找树所表示的动态集合发生变化，要反映这种变化，就要修改数据结构，但在修改的过程中还要保持二叉查找树的性质。我们将看到，插入一个元素调整树形比较简单，而删除一个元素就来的比较复杂。

      假设待插入节点是z，那么首先就需要找到插入位置，然后修改左右孩子以及父节点指针。下面是插入节点的算法：

insert(T,z)
{
	y <- NULL;
	x <- root[T];
	while (x != NULL)
	{
		y <- x;
		if (key[z] < key[x])
			x <- left[x];
		x <- right[x];
	}
	p[z] <- y;
	if (y == NULL)
		root[T] <- z;
	else if (key[z] < key[y])
		left[y] <- z;
	else right[y] <- z;
}

        对于节点的删除，应该是二叉查找树各操作中最为繁琐的了，主要分为三种情况，设被删节点为z：

        a) z是叶子节点，那么直接删除即可，并修改父节点指针；

        b) z有一个孩子，那么将其删除，并根据z是其父节点哪个孩子来把z的孩子放到适当位置；

        c) z有两个孩子，这是最复杂的一种情况，我们可以将其转换为上述两种情况的一种，即寻找z的后继节点（前驱也可以，我们 这里的实现是利用后继），然后将后继关键字复制到z中，然后删除后继节点。对于z节点的后继，它最多只可能有一个有一个孩子，而且这个孩子只可能为右孩子，随便找个图就能理解了。算法就不给了，下面直接给出二叉查找树C++实现源代码。

实现源代码

#include<iostream>

using namespace std;
template <typename T> class BSTree;

template <typename T>
class node
{
private:
	friend class BSTree<T>;
	T data;
	node *left;//左孩子
	node *right;//右孩子
	node *parent;//父节点
public:
	node(const T &d) :data(d), left(NULL), right(NULL), parent(NULL){}
	T getData()const { return data; }
	void setData(const T &d) { data = d; }
	/*省略指针域setter和getter*/
};

template <typename T>
class BSTree
{
private:
	node<T> *root;
	BSTree& operator=(const BSTree&);//只声明不实现，以禁止赋值
	BSTree(const BSTree&);//禁止复制构造
public:
	BSTree(node<T> *r) :root(r){}//构造函数，接受一个节点指针形参
	BSTree() :root(NULL){}
	bool empty()const { return root == NULL; }
	void insert(const T&);
	void create();
	node<T>* locate(const T&)const;
	void preTraversal()const;
	void inTraversal()const;
	void erase(const T&);
	void erase(node<T>*);
	node<T>* minimum()const;
	node<T>* maximum()const;
	node<T>* successor(const T&)const;//找后继
	node<T>* predecessor(const T&)const;//找前驱
	void destroy();
};

template <typename T>
void BSTree<T>::insert(const T &d)
{//插入，非递归
	node<T> *p = NULL, *curr = root;
	while (curr != NULL)
	{//找到插入位置
		p = curr;
		if (d <= curr->data)
			curr = curr->left;
		else curr = curr->right;
	}
	curr = new node<T>(d);
	if (p == NULL)//若树为空
		root = curr;
	else if (d <= p->data) p->left = curr;
	else p->right = curr;
	curr->parent = p;
}

template <typename T>
void BSTree<T>::create()
{
	T data;
	cout << "Enter the value(s),CTRL+Z to end" << endl;
	while (cin >> data)
		insert(data);
	cin.clear();
}

template <typename T>
void BSTree<T>::preTraversal()const
{//先序遍历
	node<T> *curr = root;
	if (curr != NULL)
	{
		cout << curr->data << ' ';
		BSTree LEFT(curr->left);//用左子树构建一个BSTree对象，继续递归
		LEFT.preTraversal();
		BSTree RIGHT(curr->right);
		RIGHT.preTraversal();
	}
}

template <typename T>
void BSTree<T>::inTraversal()const
{//中序遍历
	node<T> *curr = root;
	if (curr != NULL)
	{
		BSTree LEFT(curr->left);
		LEFT.inTraversal();
		cout << curr->data << ' ';
		BSTree RIGHT(curr->right);//用右子树构建一个BSTree对象，继续递归
		RIGHT.inTraversal();
	}
}

/*template <typename T>
node<T>* BSTree<T>::locate(const T &d)const
{//查找，非递归
node<T> *curr = root;
while(curr != NULL && curr->data != d)
{
if(curr->data > d)
curr = curr->left;
else curr = curr->right;
}
return curr;
}*/

template <typename T>
node<T>* BSTree<T>::locate(const T &d)const
{//查找递归版本
	node<T> *curr = root;
	if (curr == NULL || curr->data == d)
		return curr;
	else if (curr->data > d)
	{
		BSTree LEFT(curr->left);
		return LEFT.locate(d);
	}
	else
	{
		BSTree RIGHT(curr->right);
		return RIGHT.locate(d);
	}
}

/*
template <typename T>
node<T>* BSTree<T>::minimum()const
{//求最小值，非递归
	if (root == NULL) return root;
	node<T> *curr = root;
	while (curr->left != NULL)
		curr = curr->left;
	return curr;
}
*/

template <typename T>
node<T>* BSTree<T>::minimum()const
{//求最小值递归版本
	if (root == NULL) return root;
	node<T> *curr = root;
	if (curr->left == NULL) return curr;
	BSTree LEFT(curr->left);
	return LEFT.minimum();
}

/*
template <typename T>
node<T>* BSTree<T>::maximum()const
{//求最大值，非递归
	if (root == NULL) return root;
	node<T> *curr = root;
	while (curr->right != NULL)
		curr = curr->right;
	return curr;
}
*/

template <typename T>
node<T>* BSTree<T>::maximum()const
{//求最大值递归版本
	if (root == NULL) return root;
	node<T> *curr = root;
	if (curr->right == NULL) return curr;
	BSTree RIGHT(curr->right);
	return RIGHT.maximum();
}

template <typename T>
node<T>* BSTree<T>::successor(const T &d)const
{//找后继
	node<T> *p = locate(d);
	if (p->right != NULL)
	{//若右子树不为空，则后继为右子树的最小值
		BSTree RIGHT(p->right);
		return RIGHT.minimum();
	}
	node<T> *par = p->parent;
	while (par != NULL && par->right == p)
	{//若为空，则后继在沿右指针反向而上第一个拐点处
		p = par;
		par = p->parent;
	}
	return par;
}

template <typename T>
node<T>* BSTree<T>::predecessor(const T &d)const
{
	node<T> *p = locate(d);
	if (p->left != NULL)
	{//若左子树部位空，则前驱为左子树最大值
		BSTree LEFT(p->left);
		return LEFT.maximum();
	}
	node<T> *par = p->parent;
	while (par != NULL && par->left == p)
	{//若为空，则前驱在沿左指针反向而上第一个拐点处
		p = par;
		par = p->parent;
	}
	return par;
}

template <typename T>
void BSTree<T>::erase(node<T> *p)
{
	node<T> *next, *child;
	if (p->left == NULL || p->right == NULL)
		next = p;//确定删除节点，若其最多有一个子女
	else next = successor(p->data);
	if (next->left != NULL)
		child = next->left;//取被删节点的子女，用以代替其位置，它最多有一个子女
	else child = next->right;
	if (child != NULL)//被删节点有子女
		child->parent = next->parent;
	if (next->parent == NULL)//若要删除的节点为根节点
		root = child;
	else if (next == next->parent->left)//若被删节点为其父节点的左孩子
		next->parent->left = child;
	else next->parent->right = child;//若为右孩子
	if (next != p)
		p->data = next->data;
	delete next;//释放节点
}

template <typename T>
void BSTree<T>::erase(const T &d)
{//删除一个节点
	node<T> *p = locate(d);
	erase(p);
}

template <typename T>
void BSTree<T>::destroy()
{//销毁二叉树
<pre class="cpp" name="code">	if(root == NULL) return;
	if(root->left != NULL)
	{
		BSTree<T> LEFT(root->left);
		LEFT.destroy();
	}
	if(root->right != NULL)
	{
		BSTree<T> RIGHT(root->right);
		RIGHT.destroy();
	}
	delete root;
}

int main()
{//12 5 18 2 9 15 19 17
	BSTree<int> btree;
	cout << "btree.create()" << endl;
	btree.create();
	cout << "btree.inTraversal()" << endl;
	btree.inTraversal();
	btree.destroy();
	cout << "btree.inTraversal()" << endl;
	btree.inTraversal();
	getchar();
	return 0;
}

         在我们的源代码实现中，对于locate、minimum、maximum操作既给出了递归版本，也给出了非递归版本；对于erase操作给出了两个版本，一个是根据节点指针来删除，一个是根据关键字来删除，后者在查找到该节点后调用前者来实现删除。

      注意：在很多程序中，递归的时候都是直接创建左右子树的，因而对于这棵树我们最好不要定义能够销毁节点的析构函数，不然会析构子树对象，最好在程序结束时调用destroy函数。

二叉树的三种层次遍历算法

思考题 12-2 基数树