《算法导论》第三版第12章 二叉搜索树 练习&思考题 个人答案

12.1 什么是二叉搜索树

12.1-1

高度为 2:
高度为3：

高度为4：

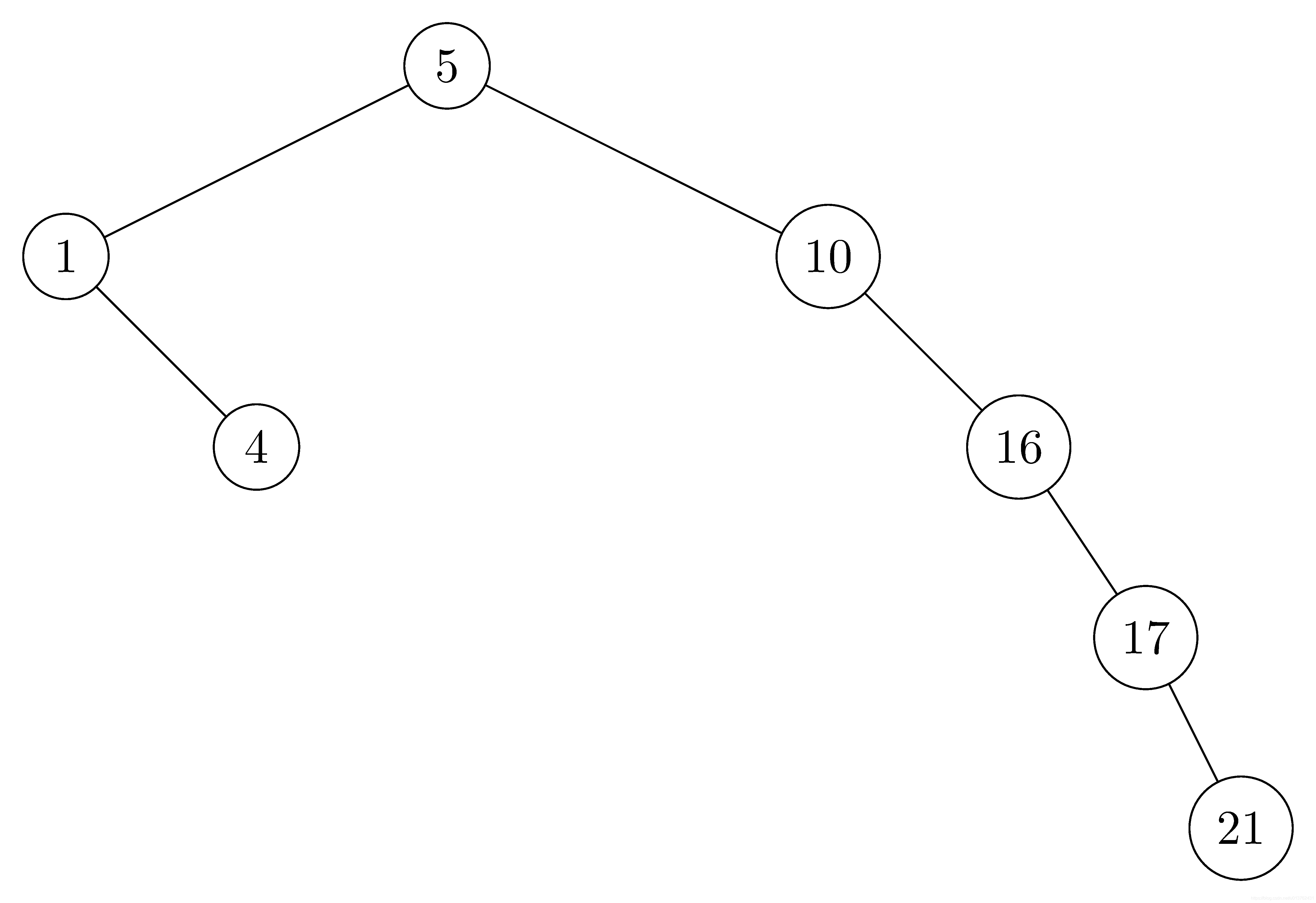
高度为5：

高度为6：

12.1-2

解：最小堆的结点值总不大于孩子结点的值，而二叉搜索树的结点值不小于左子树元素结点的值，不大于右子树元素结点的值；最小堆性质无法在O(n)时间内按序输出一棵有n个结点树的关键字，因为堆（以最小堆为例）无法告知大于当前结点的最小元素是在左子树还是在右子树。
换一个角度考虑，如果真的有这种方法，意味着存在O(n)时间的比较排序算法，而这被证明是不存在的。

12.1-3

解：

INORDER-TREE-WALK(T)
let S be an empty stack
current = T.root
done = 0
while !done
    if current != NIL
        PUSH(S, current)
        current = current.left
    else
        if !S.EMPTY()
            current = POP(S)
            print current
            current = current.right
        else done = 1

12.1-4

解：

PREORDER-TREE-WALK(x)
if x != NIL
    print x.key
    PREORDER-TREE-WALK(x.left)
    PREORDER-TREE-WALK(x.right)

POSTORDER-TREE-WALK(x)
if x != NIL
    POSTORDER-TREE-WALK(x.left)
    POSTORDER-TREE-WALK(x.right)
    print x.key

递归真的好用。

12.1-5

证明：反证法，假设我们可以使用小于$\Omega (n\lg n)$的时间，因为遍历二叉搜索树只需要$\Theta (n)$，我们就可以得到小于$\Omega (n\lg n)$的比较排序算法，这与第8章的证明相矛盾。（也就类似于12.1-3的思路了）

12.2 查询二叉搜索树

12.2-1

解：c（先找到911后找到912不可能）和e（先找到347后找到299不可能）。

12.2-2

解：

TREE-MINIMUM(x)
while x.left != NIL
    return TREE-MINIMUM(x.left)
return x

TREE-MAXIMUM(x)
while x.right != NIL
    return TREE-MAXIMUM(x.right)
return x

12.2-3

解：

TREE-PREDECESSOR(x)
if x.left != NIL
    return TREE-MAXIMUM(x.left)
y = x.p
while y != NIL and x == y.left
    x = y
    y = y.p
return y

12.2-4

思路：例如在查找过程中某一结点x的右孩子的两个孩子结点选择了右边，x的右孩子的左孩子就归到A集合，但该数还是比B集合中的x大。

12.2-5

证明：结点x的后继s一定位于x的右子树，而后继s如果有左孩子，该左孩子肯定还是位于x的右子树，那么该左孩子的值就介于x和s之间，那么s就不是x的后继了，矛盾；对称地可证明前驱没有右孩子。

12.2-6

证明：首先，我们确定$y$必须是$x$的祖先。如果$y$不是$x$的祖先，那么让$z$表示$x$和$y$的第一个共同祖先。根据二叉搜索树属性，$x<z<y$，因此$y$不能是$x$的后继。接下来注意$y.left$必须是$x$的祖先，因为如果不是，那么$y.right$将是$x$的祖先，暗示$x>y$。最后，假设$y$不是$x$的最底层祖先，其左孩子也是$x$的祖先。让$z$表示这个最底层祖先。那么$z$必须在$y$的左子树中，这意味着$z<y$，这与$y$是$x$的后继相矛盾。

12.2-7

证明（来自参考答案）：
Note that a call to $\text{TREE-MINIMUM}$ followed by $n-1$ calls to $\text{TREE-SUCCESSOR}$ performs exactly the same inorder walk of the tree as does the procedure $\text{INORDER-TREE-WALK}$. $\text{INORDER-TREE-WALK}$ prints the $\text{TREE-MINIMUM}$ first, and by
definition, the $\text{TREE-SUCCESSOR}$ of a node is the next node in the sorted order determined by an inorder tree walk.
This algorithm runs in $\Theta (n)$ time because:

It requires $O(n)$ time to do the n procedure calls.
It traverses each of the $n-1$ tree edges at most twice, which takes $O(n)$ time.

To see that each edge is traversed at most twice (once going down the tree and once going up), consider the edge between any node $u$ and either of its children, node $v$. By starting at the root, we must traverse $(u,v)$ downward from $u$ to $v$, before traversing it upward from $v$ to $u$. The only time the tree is traversed downward is in code of $\text{TREE-MINIMUM}$, and the only time the tree is traversed upward is in code of $\text{TREE-SUCCESSOR}$ when we look for the successor of a node that has no right subtree.
Suppose that is $u$'s left child.

Before printing $u$, we must print all the nodes in its left subtree, which is rooted at $v$, guaranteeing the downward traversal of edge $(u,v)$.
After all nodes in $u$'s left subtree are printed, $u$ must be printed next. Procedure $\text{TREE-SUCCESSOR}$ traverses an upward path to $u$ from the maximum element (which has no right subtree) in the subtree rooted at . This path clearly includes edge $(u,v)$, and since all nodes in $u$'s left subtree are printed, edge $(u,v)$ is never traversed again.

Now suppose that $v$ is $u$'s right child.

After $u$ is printed, $\text{TREE-SUCCESSOR}(u)$ is called. To get to the minimum element in $u$'s right subtree (whose root is $v$), the edge $(u,v)$ must be traversed downward.
After all values in $u$'s right subtree are printed, $\text{TREE-SUCCESSOR}$ is called on the maximum element (again, which has no right subtree) in the subtree rooted at $v$. $\text{TREE-SUCCESSOR}$ traverses a path up the tree to an element after $u$, since $u$ was already printed. Edge $(u,v)$ must be traversed upward on this path, and since all nodes in $u$'s right subtree have been printed, edge $(u,v)$ is never traversed again.

Hence, no edge is traversed twice in the same direction.
Therefore, this algorithm runs in $\Theta (n)$ time.

12.2-8

证明：假设$x$是起始节点，$y$是结束节点。$x$和$y$之间的距离最多为$2h$，连接$k$节点的所有边都被访问两次，因此需要$O(k+h)$时间。

12.2-9

证明：
假设$x$是$y$的左孩子，那么$y.key>x.key$，以及$y$可能有的右子树的关键字都大于$y.key$，且$x$是叶结点没有右孩子，所以$y.key$是$T$树中大于$x.key$的最小关键字；
假设$x$是$y$的右孩子，那么$y.key<x.key$，以及$y$可能有的左子树的关键字都小于$y.key$，且$x$是叶结点没有左孩子，所以$y.key$是$T$树中小于$x.key$的最大关键字。

12.3 插入和删除

12.3-1

解：

RECURSIVE-TREE-INSERT(T, z)
if T.root = NIL
    T.root = z
else INSERT(NIL, T.root, z)

INSERT(p, x, z)
if x == NIL
    z.p = p
    if z.key < p.key
        p.left = z
    else 
        p.right = z
else if z.key < x.key
    INSERT(x, x.left, z)
else 
    INSERT(x, x.right, z)

12.3-2

证明：易证路径是一样的，又因为搜索时检查的节点数也包括搜索到的节点，所以……

12.3-3

解：

TREE-SORT(A)
let T be an empty binary search tree
for i = 1 to A.length
    TREE-INSERT(A[i])
INORDER-TREE-WALK(T.root)

最坏情况：$\Theta (n^2)$ - 当重复的$\text{TREE-INSERT}$操作产生一个线性结点链时。
最好情况：$\Theta (n\lg n)$ - 当重复的$\text{TREE-INSERT}$操作产生高度为$\Theta (\lg n)$的二叉树时。

12.3-4

解：不一样

先删除A，再删除B：

  A        C        C
 / \      / \        \
B   D    B   D        D
   /
  C
先删除B，再删除A：
  A        A        D
 / \        \      /
B   D        D    C
   /        /
  C        C

12.3-5

解：

PARENT(z)
if z == NIL
    m = T.root
else 
    m = z.left
while m != x
    p = m
    m = m.right
return p

GET-PARENT(T, x)
if x.right == NIL
    if x == x.succ.left
        x.p = x.succ
    else
        z = x.succ
        x.p = PARENT(z)
else
    y = TREE-MAXIMUM(x.right)
    if x == y.succ.left
        x.p = y.succ
    else
        z = y.succ
        x.p = PARENT(z)

12.3-6

思路：可以在原函数第5行添加一个RANDOM(0,1)，返回0选择前驱，返回1选择后继即可。

12.4 随机构建二叉搜索树

12.4-1

证明：
$$\begin{array}{rl}\sum _{i=0}^{n-1}\left(\genfrac{}{}{0ex}{}{i+3}{3}\right)& =\sum _{i=0}^{n-1}\frac{(i+3)(i+2)(i+1)}{6}\\ & =\frac{1}{6}\sum _{i=0}^{n-1}{i}^3+6i^2+11i+6\\ & =\frac{1}{6}(\frac{(n-1{)}^2{n}^2}{4}+\frac{6(n-1)n(2n-1)}{6}+\frac{11n(n-1)}{2}+6n)\\ & =\frac{n(n+1)(n+2)(n+3)}{24}\\ & =\left(\genfrac{}{}{0ex}{}{n+3}{4}\right).\end{array}$$

12.4-2

证明（来自参考答案）：
We will answer the second part first. We shall show that if the average depth of a p node is $\Theta (\lg n)$, then the height of the tree is $O(n\lg n)$. Then we will answer the first part by exhibiting that this bound is tight: there is a binary search tree with p average node depth $\Theta (\lg n)$ and height $\Theta (\sqrt{n\lg n})=\omega (\lg n)$.
Lemma
If the average depth of p a node in an $n$-node binary search tree is $\Theta (\lg n)$, then the height of the tree is $O(\sqrt{n\lg n})$.
Proof
Suppose that an $n$-node binary search tree has average depth $\Theta (\lg n)$ and height $h$. Then there exists a path from the root to a node at depth $h$, and the depths of