最短路径的定义
在最短路径问题中,给出的是一个带权有向图G=(V,E),加权函数w:E->R为从边到实值的映射。路径p = <v0,v1,v2...vk>的权是其组成该路径的各边的权值之和:
定义从u到v的最短路径的权为:
从顶点u到v的最短路径为权值等于最短路径权值的任何路径。
单源路径问题的诸多变体
单终点最短路径:找出每个顶点v指向终点t的最短路径。将原有向图的每条边反向即可变为单源最短路径问题。
单对顶点之间的最短路径问题:找出顶点u到v的最短路径。若解决了u的单源最短路径问题,那么u到顶点v的最短路径也就迎刃而解了,即使在最坏情况下,在渐进意义上,还没有比这个更好的解决该问题的方法。
每对顶点间的最短路径:对任意的每对顶点u,v,找出它们之间的最短路径。可以对每个顶点u,来一次单源最短路径算法即可解决该问题。但是根据该问题的结构,可以有更好的方法予以解决,我们将在下一章讨论。
最短路径的最优子结构
最短路径是具有最优子结构的,因此有些算法采用了贪心(还得具有贪性选择性)和动态规划方法(还得有重叠子问题性质)。下面的定理更加转却的表述了最短路径的最优子结构性质。
负权边和回路
在单源最短路径问题的某些实例中,可能存在权值为负的边,特别的,如果图中存在着一个负权回路(权值和为负的环),则有些问题需要改变了。若从源点u出发不可达任何负权回路,则对于最短路径的权的定义依然正确,无需改变;但是若能够到达某一负权回路,则最短路径的权值问题就不再成立,此问题将会无解,因为对于该回路上的某顶点v,可以无限制的绕旋该回路,每次都能找到更短的最短路径。
在我们将要介绍的dijkstra算法中,要求有向图不能包含负权边;Bellman_Ford算法可以允许负权边以及源点不可到达的负权回路的存在,如果存在能够达到的负权回路,则将不能求解,但是可以报告负权回路的存在,并且找出该回路。
最短路径的表示
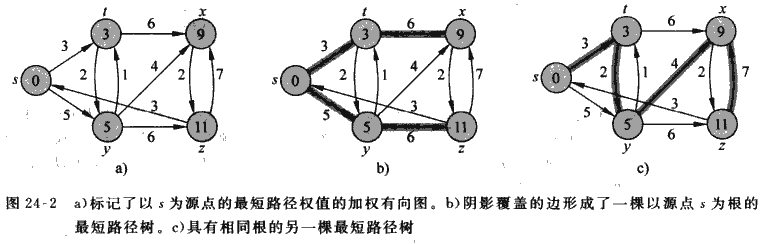
类似在第22章 图的基本算法中广度优先搜索BFS使用的,我们将用前驱数组parent来存储各个顶点的前驱。如果顶点v的前驱为u,那么设置parent[v] = u,若其不存在前驱,则设置为v本身。在算法结束之后,我们就可以得到每个顶点v到源点s的最短路径了,只是路径上的顶点是沿着s到v反向排列的。运用这个前驱数组,我们还可以构造出前驱子图Gpi = (Vpi,Epi),或者叫做最短路径树。如下图阴影部分即为前驱子图或者最短路径树。
松弛技术
本章算法采用松弛(relaxation)技术。对每个顶点v设置一个dis域,表示v到源点s的最短权值的上界,称之为最短路径估计(shortest-path estimate),在算法开始之前,采用下面的过程初始化每个顶点的相关域。
void initVertex(size_t source)
{
for (size_t i = 1; i <= nodenum; ++i)
{
V[i].dis = MAX;
V[i].p = i;
};
V[source].dis = 0;
}以下为松弛操作代码
void relax(size_t u, size_t v, int w)
{
if (V[v].dis > V[u].dis + w)
{
V[v].dis = V[u].dis + w;
V[v].p = u;
}
}在每一次的松弛边(u,v)的操作过程中,我们要测试是否能够通过u,更短的到达v,如果有,则更新dis[v]和parent[v],每一次的松弛都会减小最短路径估计的值dis[v]。关于松弛可以这样理解:松弛,是对V[v].dis <= V[u].dis + w这个表达式的松弛,每次松弛之后V[v].dis的值都会减小,那么满足该表达式就更加没有压力,意即松弛了这种压力。
本章算法如下:
#include<iostream>
#include<fstream>
#include<vector>
#include<stack>
#include<algorithm>
#include<functional>
#include"FibonacciHeap.h"
#define NOPARENT 0
#define MAX 0x7ffffff
#define MIN 0x8000000
using namespace std;
enum color{ WHITE, GRAY, BLACK };
struct edgeNode
{//边节点
size_t adjvertex;//该边的关联的顶点
int weight;//边权重
edgeNode *nextEdge;//下一条边
edgeNode(size_t adj, int w) :adjvertex(adj), weight(w), nextEdge(nullptr){}
};
struct vertex
{
size_t id;//顶点id
color c;
int dis;//距源点距离
size_t p;//父顶点
size_t s, f;//访问开始和结束时间
vertex(size_t i = 0) :id(i), p(NOPARENT), c(WHITE),dis(0),s(0),f(0){}
};
class AGraph
{//有向图
private:
vector<edgeNode*> E;
vector<vertex> V;
size_t nodenum;
void initVertex(size_t source)
{
for (size_t i = 1; i <= nodenum; ++i)
{
V[i].dis = MAX;
V[i].p = i;
};
V[source].dis = 0;
}
void relax(size_t u, size_t v, int w)
{
if (V[v].dis > V[u].dis + w)
{
V[v].dis = V[u].dis + w;
V[v].p = u;
}
}
void printSP(size_t v)
{
if (v != V[v].p)
{
printSP(V[v].p);
cout << " --> " << v;
}
else cout << v;
}
void printASP()
{
for (size_t i = 1; i <= nodenum; ++i)
{
printSP(i);
cout << '\t' << V[i].dis << endl;
}
cout << endl;
}
size_t vertexIndex(size_t vertex_id)
{
size_t index;
for (size_t i = 1; i <= nodenum; ++i)
if (V[i].id == vertex_id) index = i;
return index;
}
void SPT(AGraph*);
void printCycle(size_t);
void DFS();
void DFS_aux_Not_recursive(size_t, size_t&);
public:
AGraph(size_t n = 0) :nodenum(n) { editGraph(n); }
void editGraph(size_t n)
{
V.resize(n + 1);
E.resize(n + 1);
for (size_t i = 1; i <= nodenum; ++i)
V[i].id = i;
}
void initGraph();//初始化有向图
edgeNode* search(size_t, size_t);//查找边
void addEdge(size_t, size_t, int);//有向图中添加边
void deleteEdge(size_t, size_t);//有向图中删除边
bool Bellman_Ford(size_t,AGraph*);
void dagSP(size_t);
void dijkstra(size_t,AGraph *);
void topSort(vector<size_t>&);
void print();
~AGraph();
};
void AGraph::initGraph()
{
size_t start, end;
int w;
ifstream infile("F:\\djikstra.txt");
while (infile >> start >> end >> w)
addEdge(start, end, w);
}
edgeNode* AGraph::search(size_t start, size_t end)
{
edgeNode *curr = E[start];
while (curr != nullptr && curr->adjvertex != end)
curr = curr->nextEdge;
return curr;
}
void AGraph::addEdge(size_t start, size_t end, int weight = 1)
{
edgeNode *curr = search(start, end);
if (curr == nullptr)
{
edgeNode *p = new edgeNode(end, weight);
p->nextEdge = E[start];
E[start] = p;
}
}
void AGraph::deleteEdge(size_t start, size_t end)
{
edgeNode *curr = search(start, end);
if (curr != nullptr)
{
if (curr->adjvertex == end)
{
E[start] = curr->nextEdge;
delete curr;
}
else
{
edgeNode *pre = E[start];
while (pre->nextEdge->adjvertex != end)
pre = pre->nextEdge;
pre->nextEdge = curr->nextEdge;
delete curr;
}
}
}
void AGraph::SPT(AGraph *spt)
{//根据前驱子图构造最短路径树
for (size_t i = 1; i <= nodenum; ++i)
{
size_t j = i;
while (j != V[j].p)
{
edgeNode *curr = search(V[j].p, j);
spt->addEdge(V[j].p, j, curr->weight);
j = V[j].p;
}
}
}
void AGraph::printCycle(size_t cycle)
{//求负权回路,时间复杂度O(V)
vector<color> onCycle(nodenum + 1);
for (size_t i = 1; i <= nodenum; ++i)
onCycle[i] = WHITE;//顶点全部初始化为白色
while (onCycle[cycle] == WHITE)
{//当遇到黑色顶点时退出,表明此时是第二次扫描到,可断定该顶点必在回路上
onCycle[cycle] = BLACK;
cycle = V[cycle].p;
}
while (onCycle[cycle] == BLACK)
{//以该顶点为起点,开始输出回路上的顶点
onCycle[cycle] = WHITE;
cout << cycle << ' ';
cycle = V[cycle].p;
}
}
bool AGraph::Bellman_Ford(size_t source,AGraph *spt)
{//Bellman-Ford算法计算单源最短路径,spt存储最短路径树SPT
initVertex(source);
for (size_t i = 1; i != nodenum; ++i)
{//进行V-1此迭代
for (size_t j = 1; j != E.size(); ++j)
{//每次都对所有边进行一次松弛
edgeNode *curr = E[j];
while (curr != nullptr)
{
relax(j, curr->adjvertex, curr->weight);
curr = curr->nextEdge;
}
}
}
for (size_t j = 1; j != E.size(); ++j)
{//判断是否有负权回路
edgeNode *curr = E[j];
while (curr != nullptr)
{
if (V[curr->adjvertex].dis > V[j].dis + curr->weight)
{//有则打印出该回路,并终止程序
printCycle(curr->adjvertex);
cout << endl;
return false;
}
curr = curr->nextEdge;
}
}
SPT(spt);//否则计算出最短路径树
return true;
}
void AGraph::dagSP(size_t source)
{//有向无环图求单源最短路径
vector<size_t> topsort;
topSort(topsort);//先进行拓扑排序,并将拓扑顺序的顶点标号存入topsort
initVertex(source);//初始化顶点的距离和父顶点
for (size_t i = 0; i != topsort.size(); ++i)
{//按拓扑顺序
edgeNode *curr = E[topsort[i]];
while (curr != nullptr)
{//对每个顶点的边进行一次松弛
relax(topsort[i], curr->adjvertex, curr->weight);
curr = curr->nextEdge;
}
}
for (size_t i = 0; i != topsort.size(); ++i)
{
size_t index = vertexIndex(topsort[i]);
cout << topsort[i] << '\t' << V[index].dis << endl;
}
//SPT(spt);//这里最好不要构造最短路径树了,若要构造,则需对SPT进行些许修改,
//因为顶点编号和索引不在对应,在排序过程中移动了。
}
void AGraph::dijkstra(size_t source,AGraph *spt)
{//dijkstra算法求单源最短路径,只适用于非负权值无回路图,斐波那契堆实现
initVertex(source);
fibonacci_heap<int, size_t> Q;
vector<fibonacci_heap_node<int,size_t>*> ptr_fibo_node(nodenum + 1);//顶点所关联的堆结点地址
for (size_t i = 1; i <= nodenum; ++i)
ptr_fibo_node[i] = Q.insert(V[i].dis, i);
while (!Q.empty())
{
pair<int, size_t> min = Q.extractMin();//取得当前离远点最近顶点
ptr_fibo_node[min.second] = nullptr;//置空,表明堆中已删除该顶点
edgeNode *curr = E[min.second];
while (curr != nullptr)
{
relax(min.second, curr->adjvertex, curr->weight);
if (ptr_fibo_node[curr->adjvertex] != nullptr && //如果该顶点到源点距离减小
V[curr->adjvertex].dis < ptr_fibo_node[curr->adjvertex]->key)
Q.decreaseKey(ptr_fibo_node[curr->adjvertex], V[curr->adjvertex].dis);
curr = curr->nextEdge;
}
}
SPT(spt);//根据前驱子图求得最短路径树邻接表
printASP();//打印源点到各顶点路径及最小权值和
}
inline void AGraph::print()
{
for (size_t i = 1; i != E.size(); ++i)
{
edgeNode *curr = E[i];
cout << i;
if (curr == nullptr) cout << " --> null";
else
while (curr != nullptr)
{
cout << " --" << "<" << curr->weight << ">--> " << curr->adjvertex;
curr = curr->nextEdge;
}
cout << endl;
}
}
void AGraph::DFS_aux_Not_recursive(size_t u, size_t &time)
{
stack<size_t> S;
vector<edgeNode*> access_edge(E);//记下每个顶点下一条将被访问的边
V[u].c = GRAY;
V[u].s = ++time;
S.push(u);
while (!S.empty())
{//只要栈不空,不断访问
size_t i = S.top();
edgeNode *curr = access_edge[i];//得到顶点i当前将要被访问的边
while (curr != nullptr)
{//不断循环,直到访问到一个白节点,或者顶点i的所有邻接点已被访问
if (V[curr->adjvertex].c == WHITE)
{//与i相邻的是白节点,即未被访问过
V[curr->adjvertex].c = GRAY;
V[curr->adjvertex].s = ++time;
S.push(curr->adjvertex);//访问后入栈
access_edge[i] = curr->nextEdge;//记下顶点i下一条将要被访问的边
break;
}
else curr = curr->nextEdge;
}
if (curr == nullptr)
{//顶点i的所有邻接点已被访问,则出栈
V[i].c = BLACK;
V[i].f = ++time;
S.pop();
}
}
}
void AGraph::DFS()
{
size_t time = 0;
for (size_t i = 1; i != E.size(); ++i)
if (V[i].c == WHITE)
DFS_aux_Not_recursive(i, time);
}
void AGraph::topSort(vector<size_t> &topsort)
{
struct vertexCompare
{
bool operator()(const vertex &lhs, const vertex &rhs)const
{
return lhs.f > rhs.f;
}
};
DFS();
sort(++V.begin(), V.end(), vertexCompare());
for (size_t i = 1; i != V.size(); ++i)
topsort.push_back(V[i].id);
}
AGraph::~AGraph()
{
for (size_t i = 1; i != E.size(); ++i)
{
edgeNode *curr = E[i], *pre;
while (curr != nullptr)
{
pre = curr;
curr = curr->nextEdge;
delete pre;
}
}
}
const int nodenum = 5;
int main()
{
AGraph graph(nodenum),spt(nodenum);
graph.initGraph();
graph.print();
cout << endl;
graph.dijkstra(1, &spt);
spt.print();
getchar();
return 0;
}
Bellman-Ford算法
1、调用initVertex初始化各个顶点,包括dis域和前驱域;
2、对所有边进行松弛,连续进行|V| - 1次;
3、对所有边进行一次检测,判断是否有环,有则调用printCycle输出此环,并退出;
4、根据前驱数组,构造出最短路径树(SPT)。
习题 24.1-5
题目意思是计算每个顶点到其他顶点的各条最短路径中的最小权值?!O(VE)算法,求思路?
习题 24.1-6
具体代码见上述printCycle函数,思路:当出现d[v] > d[u] + w(u,v)时,说明顶点u和v均受到了负权回路对最短路径权值的影响,但并不能说明u或者v就在此回路上。我们可以从u或者v开始,根据前驱数组找到位于该环上的任意顶点,然后再从该顶点开始根据前去数组逆推得到该环,算法如下:
1、从顶点u后者v开始根据前驱数组逆推,直到两次遇到同一个顶点,记为x,那么x必在此环上;
2、重新以x为起点根据前驱数组逆推,依次输出各顶点,直到再次遇到x则停止,即求得该环。
有向无回路图的单源最短路径
有向无回路图(dag)G可以根据其结构特点——无回路——构造出线性时间的单元最短路径算法,如下:
1、首先对G进行拓扑排序得到拓扑序列;
2、根据拓扑序列一次对每个顶点的邻接边进行松弛。
具体代码见上述dagSP函数。
习题 24.2-2
最后一个顶点没有出边,因而无所谓松不松弛。
习题 24.2-3
松弛条件改为“d[v] < d[u] + w(v)”,初始化时对每个顶点v,d[v] = 0.
Dijkstra算法
Dijkstra算法是一个贪心算法,算法伪代码如下:
Dijkstra(G, s)
{
initVertex(G, s);
Q <- V[G];
S <- NULL;
while (Q != NULL)
{
u <- EXTRACT - MIN(Q);
S <- S + {u};
for each v in Adj[u]
relax(u, v, w(u, v));
}
}








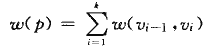
















 1302
1302

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








