前些日子刷完了leetcode的1-20题,现在来一个总结!!!

目录
1. 两数之和【简单】
这道题给定一个数组 以及一个目标数,返回两个数之和等于这个目标数的索引。
这个题首先会想到量词循环遍历,但是这样一来时间复杂度就变成了的O(n2)
这个提供一个时间复杂度为 O(n)的解法
牺牲空间换时间
思路:查找时,建立索引。本题的缓存可在找的过程中建立索引,故一个循环可以求出。


2. 两数相加【中等】

思路:数字进位问题,该位有效值为值%10,进位值为值/10。可以使用一个变量记录进位值。
注意:最后如果进位大于0,要再链上一个进位节点。


3. 无重复字符的最长子串【中等】

思路:其实只需要前面出现过的重复字符的下标即可算出此段不重复子段的长度,核心操作其实是向前检索重复字符。需要注意的是最后循环
完成后,需要再算一下没有计算的那段的长度,在这些子段中取最长的。

这里重点是j的取值
两种情况
①如果重复元素在j对应坐标的后面,那么,j取重复元素坐标值+1;
②如果重复元素在j对应坐标的前面,那么j的值不变。
【例1】abcabcbb
初始值j=0;
| i | sc[i] | map | maxLen | j |
|---|---|---|---|---|
| 0 | a | <a,0> | 0 | 0 |
| 1 | b | <a,0><b,1> | 0 | 0 |
| 2 | c | <a,0><b,1><c,2> | 0 | 0 |
| 3 | a | <a,3><b,1><c,2> | 3 | 1 |
| 4 | b | <a,3><b,4><c,2> | 3 | 2 |
| 5 | c | <a,3><b,4><c,5> | 3 | 3 |
| 6 | b | <a,3><b,6><c,5> | 3 | 5 |
| 7 | b | <a,3><b,7><c,5> | 3 | 7 |
8-7<3
所以 maxLen=3
【例】abba
| i | sc[i] | map | maxLen | j |
|---|---|---|---|---|
| 0 | a | <a,0> | 0 | 0 |
| 1 | b | <a,0><b,1> | 0 | 0 |
| 2 | b | <a,0><b,2> | 2 | 2 |
| 3 | a | <a,3><b,2> | 2 | 2 |
4-2=2=2
所以 maxLen=2;

4. 寻找两个有序数组的中位数【困难】——两个数组中第k的数

思路:
首先明确什么是中位数
对于一个有n的元素的数组a[n],无论n是奇数还是偶数,其中位数为第(n-1)/2大的数与第a[n/2]大的数的平均数。
所以我们要求出第第(n-1)/2大的数与第a[n/2]大的数
下面就需要讨论怎么求两个数组中第k大的数。
就简单地方法当然就是直接归并了,时间复杂度为O(m+n)
class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int n=nums1.length+nums2.length;
return (getKth(nums1,nums2,(n-1)/2+1)+getKth(nums1,nums2,n/2+1))/2.0;
}
//采用归并排序
public int getKth(int[] nums1,int[] nums2,int k){
int m=nums1.length;
int n=nums2.length;
int[] result=new int[m+n];
int pos=0;
int i=0,j=0;
for(i=0,j=0;i<m&&j<n;){
if(nums1[i]<nums2[j]){
result[pos]=nums1[i];
i++;
pos++;
}
else{
result[pos]=nums2[j];
j++;
pos++;
}
}
while(i<m){
result[pos]=nums1[i];
i++;
pos++;
}
while(j<n){
result[pos]=nums2[j];
j++;
pos++;
}
System.out.println(result[n+m-k]);
return result[n+m-k];
}
}

结果慢的不要要的了!!!事实上这并不符合要求
但是有更快的方法,时间复杂度接近于O(log(m +n)),接下来介绍这种方法。
public class Solution {
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
int m = nums1.length, n = nums2.length;
int l = (m + n + 1) >> 1;
int r = (m + n + 2) >> 1;
return (getkth(nums1, 0, nums2, 0, l) + getkth(nums1, 0, nums2, 0, r)) / 2.0;
}
public double getkth(int[] A, int aStart, int[] B, int bStart, int k) {
if (aStart == A.length) return B[bStart + k - 1];
if (bStart == B.length) return A[aStart + k - 1];
if (k == 1) return Math.min(A[aStart], B[bStart]);
int aMid = Integer.MAX_VALUE, bMid = Integer.MAX_VALUE;
if (aStart + k/2 - 1 < A.length) aMid = A[aStart + k/2 - 1];
if (bStart + k/2 - 1 < B.length) bMid = B[bStart + k/2 - 1];
if (aMid < bMid)
return getkth(A, aStart + k/2, B, bStart, k - k/2);
else
return getkth(A, aStart, B, bStart + k/2, k - k/2);
}
}

5. 最长回文子串【中等】

思路:
首先,有一个变量记录当前最长子串str,有一个变量记录当前最长长度maxLen
从中心出发向两边扩展情况
①偶数情况
②奇数情况发
从头开到尾遍历。
class Solution {
public String longestPalindrome(String s) {
char[] ch=s.toCharArray();
int n=ch.length;
String str="";
int maxLen=0;
if(n==0){
return "";
}
if(n==1){
return s;
}
str=s.substring(0,1);
maxLen=1;
for(int i=1;i<n;i++){
//从当前位置开始扩散
//奇数情况
int k1=1;
while(i-k1>=0&&i+k1<n){
if(ch[i-k1]==ch[i+k1]){
if(maxLen<=2*k1+1){
str=s.substring(i-k1,i+k1+1);
maxLen=2*k1+1;
}
k1++;
}
else{
break;
}
}
//偶数情况
int k2=1;
while(i-k2>=0&&i+k2-1<n){
if(ch[i-k2]==ch[i+k2-1]){
if(maxLen<=2*k2){
str=s.substring(i-k2,i+k2);
maxLen=2*k2;
}
k2++;
}
else{
break;
}
}
}
return str;
}
}

另一种写法思路一样的。
public class Solution {
private int lo, maxLen;
public String longestPalindrome(String s) {
int len = s.length();
if (len < 2)
return s;
for (int i = 0; i < len - 1; i++) {
extendPalindrome(s, i, i);
extendPalindrome(s, i, i + 1);
}
return s.substring(lo, lo + maxLen);
}
private void extendPalindrome(String s, int j, int k) {
while (j >= 0 && k < s.length() && s.charAt(j) == s.charAt(k)) {
j--;
k++;
}
if (maxLen < k - j - 1) {
lo = j + 1;
maxLen = k - j - 1;
}
}
}

6. Z字形变换【中等】


这题又叫找规律题 哈哈哈哈!!!

对于这种题 用笔找到规律即可
思路:
将字符分组,每m=numRows×2-2个字符为一组
一共有n/m+1组。j为行号
对于第一行j=0,输出每组第一个元素i%m=0的元素
j=1到j=numRows-2
对于2到numRows-1行,输出 i%m=j的元素和i%m=2×numRows-j-1的元素
j=numRows-1
对于最后一行,输出每组第一个元素i%m=numRows-1的元素
class Solution {
public String convert(String s, int numRows) {
int m=numRows*2-2;
char ch[]=s.toCharArray();
int n=ch.length;
String str="";
if(m==0){
return s;
}
for(int k=0;k<n/m+1;k++){
if(k*m<n){
str+=ch[k*m];
}
}
for(int j=1;j<numRows-1;j++){
for(int k=0;k<n/m+1;k++){
if(k*m+j<n){
str+=ch[k*m+j];
}
if(k*m+2*numRows-j-2<n){
str+=ch[k*m+2*numRows-j-2];
}
}
}
for(int k=0;k<n/m+1;k++){
if(k*m+numRows-1<n){
str+=ch[k*m+numRows-1];
}
}
return str;
}
}

7. 整数反转【简单】
这题可以构成其他算法的一小部分,背下来把!!!


class Solution {
public int reverse(int x) {
int result=0;
while(x!=0){
int tail=x%10;//尾数
int newResult=result*10+tail;
if((newResult-tail)/10!=result) return 0;
result=newResult;
x=x/10;
}
return result;
}
}
- 字符串转换整数(中等)



题目要求提炼:
①如果字符串为空返回0
②过滤无用的开头空格字符,找到第一个非空元素
1)如果这时候i索引=n那么,表示只有空格,返回0
2)如果第一个非空字符为非+,-和数字,返回0
3)如果第一个非空字符为+或者-号,则与后面尽可能多的数字连起。
4)如果第一个非空字符是数字,则与后面尽可能多的数字连起。
情况3)4)中判断数值是否超过存储范围 如果数值超过这个范围,返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
public class Solution {
public int myAtoi(String str) {
if (str == null || str.length() == 0)
return 0;//
str = str.trim();
if(str.length()==0){
return 0;
}
char firstChar = str.charAt(0);
int sign = 1, start = 0, len = str.length();
long sum = 0;
if (firstChar == '+') {
sign = 1;
start++;
} else if (firstChar == '-') {
sign = -1;
start++;
}
for (int i = start; i < len; i++) {
if (!Character.isDigit(str.charAt(i)))
return (int) sum * sign;
sum = sum * 10 + str.charAt(i) - '0';
if (sign == 1 && sum > Integer.MAX_VALUE)
return Integer.MAX_VALUE;
if (sign == -1 && (-1) * sum < Integer.MIN_VALUE)
return Integer.MIN_VALUE;
}
return (int) sum * sign;
}
}
9. 回文数【简单】

class Solution {
public boolean isPalindrome(int x) {
//负数直接返回false
int y=x;
if(x<0){
return false;
}
//反转
int result=0;
while(x!=0){
int tail=x%10;//尾数
int newResult=result*10+tail;
if((newResult-tail)/10!=result) return false;
result=newResult;
x=x/10;
}
if(result==y){
return true;
}
return false;
}
}

public class Solution {
public boolean isPalindrome(int x) {
if (x<0 || (x!=0 && x%10==0)) return false;
int rev = 0;
while (x>rev){
rev = rev*10 + x%10;
x = x/10;
}
return (x==rev || x==rev/10);
}
}

10. 正则表达式【困难】——动态规划



提要:‘.’匹配单个字符,’*'匹配一个或多个前面的那个字符
思路:
这道题典型的动态规划
dp[n+1][m+1]
dp[i][j]:表示s从0-i 与p 0-j是否匹配
首先
初始化
| dp | 值 |
|---|---|
| dp[0][0] | true |
| dp[i][0](i≠0 ) | false |
| dp[0][j] (j≠0) | p[j]为.或者为字母 :dp[0][j]=flase;p[j]为# :dp[0][j]=dp[0][j-2] |
关系式:
| 情况 | dp[i][j]值 |
|---|---|
| p.chaAt(j-1)==’.’ | dp[i-1][j-1] |
| p.chaAt(j-1)==s.charAt(i-1) | dp[i-1][j-1] |
| p.charAt(j-1)==’*’ | 符合以下情况 (1)代表配0个字符 dp[i][j-2] (2)代表前面的n个字符(p.charAt(j-2)=s.charAt(i-1)或p.charAt(j-2)=’.’)&&dp[i-1][j] |
class Solution {
public boolean isMatch(String s, String p) {
int n=s.length();
int m=p.length();
boolean dp[][]=new boolean[n+1][m+1];
//初始化
dp[0][0]=true;
for(int i=1;i<n+1;i++){
dp[i][0]=false;
}
for(int j=1;j<m+1;j++){
if(p.charAt(j-1)=='*'){
dp[0][j]=dp[0][j-2];
}
else{
dp[0][j]=false;
}
}
for(int i=1;i<n+1;i++){
for(int j=1;j<m+1;j++){
if(p.charAt(j-1)=='.'||p.charAt(j-1)==s.charAt(i-1)){
dp[i][j]=dp[i-1][j-1];
}
else if(p.charAt(j-1)=='*'){
dp[i][j]=dp[i][j-2]||((p.charAt(j-2)==s.charAt(i-1)||p.charAt(j-2)=='.')&&dp[i-1][j]);
}
}
}
return dp[n][m];
}
}

11. 盛水最多的容器【中等】


思路:找到两个柱子之间的水平距离distance以及两个柱子的最小值height ,容积为distance*height
设置两个指针 i,j
i=0;j=n-1;
两个指针分别从左到右,和从右到左进行扫描
记录当前的最大值为maxValue;
为了提高效率,可以进行剪枝,排除一些情况,
如果 height[i]<height[j]; i++
否则 j++;
public class Solution {
public int maxArea(int[] height) {
int n = height.length;
int max = 0;
int i = 0, j = n - 1;
while(i < j) {
max = Math.max(Math.min(height[i], height[j]) * (j - i), max);
if(height[i] < height[j]) {
++i;
} else {
--j;
}
}
return max;
}
}

12. 整数转罗马数字




public class Solution {
public String intToRoman(int num) {
String M[] = {"", "M", "MM", "MMM"};
String C[] = {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"};
String X[] = {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"};
String I[] = {"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"};
return M[num/1000] + C[(num%1000)/100] + X[(num%100)/10] + I[num%10];
}
}

13. 罗马数转整数【简单】




class Solution13 {
public int romanToInt(String s) {
Map<String, Integer> map = new HashMap<>();
map.put("I", 1);
map.put("IV", 4);
map.put("V", 5);
map.put("IX", 9);
map.put("X", 10);
map.put("XL", 40);
map.put("L", 50);
map.put("XC", 90);
map.put("C", 100);
map.put("CD", 400);
map.put("D", 500);
map.put("CM", 900);
map.put("M", 1000);
int ans = 0;
for(int i = 0;i < s.length();) {
if(i + 1 < s.length() && map.containsKey(s.substring(i, i+2))) {
ans += map.get(s.substring(i, i+2));
i += 2;
} else {
ans += map.get(s.substring(i, i+1));
i ++;
}
}
return ans;
}
}

14. 最长公共前缀【简单】

public class Solution {
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0)
return "";
if (strs.length == 1)
return strs[0];
StringBuilder sb = new StringBuilder();
int n = Integer.MAX_VALUE;
boolean finished = false;
for (int i = 0; i < strs.length; ++i)
n = Math.min(strs[i].length(), n);
for (int i = 0; i < n; ++i) {
char c = strs[0].charAt(i);
for (int j = 1; j < strs.length; ++j) {
if (strs[j].charAt(i) != c) {
finished = true;
break;
}
}
if (finished)
break;
sb.append(c);
}
return sb.toString();
}
}

15. 三数之和【中等】

class Solution {
public static List<List<Integer>> threeSum(int[] nums) {
List<List<Integer>> ans = new ArrayList();
int len = nums.length;
if(nums == null || len < 3) return ans;
Arrays.sort(nums); // 排序
for (int i = 0; i < len ; i++) {
if(nums[i] > 0) break; // 如果当前数字大于0,则三数之和一定大于0,所以结束循环
if(i > 0 && nums[i] == nums[i-1]) continue; // 去重
int L = i+1;
int R = len-1;
while(L < R){
int sum = nums[i] + nums[L] + nums[R];
if(sum == 0){
ans.add(Arrays.asList(nums[i],nums[L],nums[R]));
while (L<R && nums[L] == nums[L+1]) L++; // 去重
while (L<R && nums[R] == nums[R-1]) R--; // 去重
L++;
R--;
}
else if (sum < 0) L++;
else if (sum > 0) R--;
}
}
return ans;
}
}

16. 最接近的三数之和【中等】

public class Solution {
public int threeSumClosest(int[] nums, int target) {
int min=Integer.MAX_VALUE;
int len=nums.length;
int r=0;
Arrays.sort(nums);//排序
if(len==0) {
r=0;
}else if(len==1){
r=nums[0];
}else if(len==2) {
r=nums[0]+nums[1];
}else {
r=nums[0]+nums[1]+nums[2];
}
for(int i=0;i<len;i++) {
int L=i+1;
int R=len-1;
while(L<R) {
int value=nums[i]+nums[L]+nums[R];
int tap=Math.abs(target-value);
if(tap<min) {
min=tap;
r=value;
}
if(min==0) {
return r;
}
else if(target<value) {
R--;
}else if(target>value) {
L++;
}
}
}
return r;
}
}

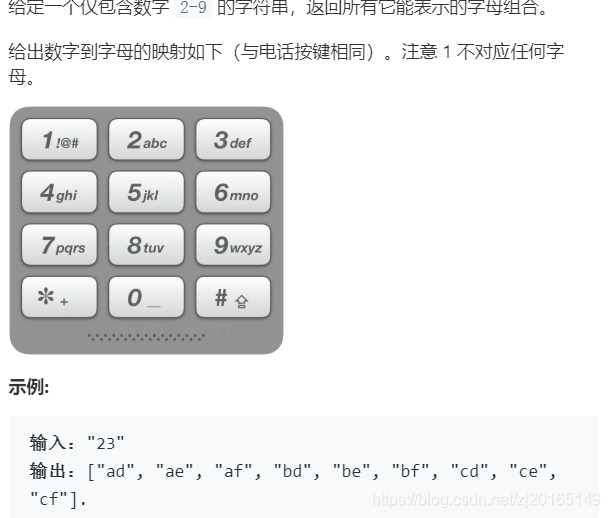
17. 电话号码的字母组合【中等】——回溯
class Solution17 {
Map<String,String> map=new HashMap<String,String> ();
List<String> list=new ArrayList<String>();
public List<String> letterCombinations(String digits) {
map.put("2", "abc");
map.put("3", "def");
map.put("4", "ghi");
map.put("5", "jkl");
map.put("6", "mno");
map.put("7", "pqrs");
map.put("8", "tuv");
map.put("9", "wxyz");
backtrack("",digits);
if(digits.length()==0){
return new ArrayList<String>();
}
return list;
}
private void backtrack(String combination,String next_digits) {
if(next_digits.length()==0) {
list.add(combination);
}
else {
//取下一个数
String str=map.get(next_digits.substring(0,1));
int len=str.length();
for(int i=0;i<len;i++) {
backtrack(combination+str.substring(i,i+1), next_digits.substring(1));
/*
* String s=combination;
* combination+=str.substring(i,i+1);
* backtrack(combination, next_digits.substring(1));
* combination=s;
*/
}
}
}
}

18. 四数之和【中等】

import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
public class Solution18 {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list=new ArrayList<List<Integer>>();
int len=nums.length;
Arrays.sort(nums);
for(int i=0;i<len;i++) {
for(int j=i+1;j<len;j++) {
int L=j+1;
int R=len-1;
while(L<R) {
int value=nums[i]+nums[j]+nums[L]+nums[R];
if(value==target) {
List<Integer> l=new ArrayList<Integer>();
l.add(nums[i]);
l.add(nums[j]);
l.add(nums[L]);
l.add(nums[R]);
if(!list.contains(l)) {
list.add(l);
}
L++;
R--;
}
else if (value<target) {
L++;
}else {
R--;
}
}
}
}
return list;
}
}
public class Solution {
public List<List<Integer>> fourSum(int[] nums, int target) {
List<List<Integer>> list=new ArrayList<List<Integer>>();
int len=nums.length;
Arrays.sort(nums);
for(int i=0;i<len;i++) {
for(int j=i+1;j<len;j++) {
int L=j+1;
int R=len-1;
while(L<R) {
int value=nums[i]+nums[j]+nums[L]+nums[R];
if(value==target) {
List<Integer> l=new ArrayList<Integer>();
l.add(nums[i]);
l.add(nums[j]);
l.add(nums[L]);
l.add(nums[R]);
if(!list.contains(l)) {
list.add(l);
}
L++;
R--;
}
else if (value<target) {
L++;
}else {
R--;
}
}
}
}
return list;
}
}

19. 删除链表中的倒数第N个节点【中等】——链表

/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode(int x) { val = x; }
* }
*/
public class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if(head.next == null) {
return null;
}
int i = 0;
ListNode p1 = head, p2 = head;
while(p1.next != null) {
p1 = p1.next;
++i;
if(i > n) {
p2 = p2.next;
}
}
if(i == n - 1) {
head = head.next;
} else {
p2.next = p2.next.next;
}
return head;
}
}

20. 有效的括号【简单】——堆

public class Solution {
public boolean isValid(String s) {
Stack<Character> stack=new Stack<Character>();
int len=s.length();
for(int i=0;i<len;i++) {
if(s.charAt(i)=='['||s.charAt(i)=='('||s.charAt(i)=='{') {
stack.push(s.charAt(i));
}else if (s.charAt(i)==']') {
//从栈中取出一个元素
if(stack.empty()==true){
return false;
}
char ch=stack.pop();
if(ch!='[') {
return false;
}
}else if(s.charAt(i)==')') {
if(stack.empty()==true){
return false;
}
char ch=stack.pop();
if(ch!='(') {
return false;
}
}else if(s.charAt(i)=='}'){
if(stack.empty()==true){
return false;
}
char ch=stack.pop();
if(ch!='{') {
return false;
}
}
}
if(stack.empty()==true) {
return true;
}
return false;
}
}























 1261
1261

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








