【机器学习入门】6.1 贝叶斯决策论：从概率到最优决策

原创已于 2025-09-06 11:38:54 修改 · 626 阅读

17 ·

CC 4.0 BY-SA版权

文章标签：

#人工智能 #机器学习 #回归 #深度学习 #kmeans

于 2025-09-05 16:39:06 首次发布

Python 同时被 3 个专栏收录

30 篇文章

订阅专栏

MODLE

28 篇文章

订阅专栏

机器学习

24 篇文章

订阅专栏

在机器学习的概率框架中，贝叶斯决策论（Bayesian Decision Theory） 是实现 “最优决策” 的核心基础 —— 尤其是在分类任务中，当我们已知所有相关概率时，它能结合 “误判损失” 帮我们选择最合理的类别标记。对于刚入门的同学来说，贝叶斯决策论的本质是 “用概率解决不确定性问题”，而要理解它，我们需要从 “概率的两种思考方式” 开始，逐步过渡到核心定理与实际应用。

1. 先搞懂：为什么需要贝叶斯？从 “抽奖” 看概率的两类问题

要理解贝叶斯决策论，先从一个简单的生活场景切入 ——抽奖。通过这个例子，我们能清晰区分 “传统概率” 和贝叶斯关注的 “逆概率”，这是入门的关键。

1.1 第一类概率：已知 “全貌”，算 “局部”（频率概率）

假设抽奖桶里有 10 个球：2 个白球（中奖）、8 个黑球（不中奖）。现在让你随机摸 1 个，问 “摸到白球（中奖）的概率是多少？”

这是我们小学就接触的 “频率概率”—— 已知总体的分布（桶里球的总数和颜色比例），计算 “某个具体事件发生的概率”。根据频率概率公式，中奖概率 = 白球数量 / 总球数 = 2/10 = 20%。

这类问题的特点是：总体信息已知，只需通过 “计数” 或 “比例” 就能算出概率，逻辑直接且直观。

1.2 第二类概率：已知 “局部观察”，推 “全貌”（逆概率）

但现实中，我们很少能知道 “总体的全貌”。比如换个场景：你不知道抽奖桶里有多少白球、多少黑球，只能先摸出 1 个球（比如摸出的是白球），然后根据这个 “观察结果”，反过来预测 “桶里白球和黑球的比例大概是多少？”

这就是贝叶斯定理要解决的逆概率问题—— 已知 “某个事件的结果（摸出白球）”，反推 “导致这个结果的原因（桶里白球比例高）” 发生的概率。

而机器学习的核心任务（比如分类、预测），本质上就是 “逆概率问题”：比如根据一张图片的像素（观察结果），反推 “这张图片是猫还是狗（原因 / 类别）” 的概率；根据用户的购买记录（观察结果），反推 “用户是否会购买下一个商品（原因 / 行为）” 的概率。

2. 为什么贝叶斯在现实中 “离不开”？

刚入门的同学可能会问：“既然传统频率概率能用，为什么还要学贝叶斯？” 答案很简单：现实中的问题，90% 以上都是 “逆概率问题”，传统频率概率根本用不了。

举几个贴近生活的例子：

天气预报：说明天降雨概率 30%。我们不可能 “重复过 100 次明天”，再统计其中 30 次下雨 —— 只能根据过去的气温、湿度、云层数据（观察结果），反推 “明天下雨（原因）” 的概率，这就是贝叶斯的应用。
日常决策：比如 “要不要买某只股票”“新产品会不会受欢迎”“下周饭菜买什么菜”—— 这些问题都没有 “已知的总体分布”，只能通过 “过去的经验 / 数据（观察结果）”，反推 “某个结果发生的概率”，再做决策。

贝叶斯定理的价值，就在于它给了我们一套 “用过去的数据 / 经验，预测未来概率” 的科学方法，让我们在 “不确定” 的世界里，能做出更合理的选择。

3. 贝叶斯定理：数学表达与核心概念

理解了 “逆概率” 的需求后，我们来看贝叶斯定理的数学公式 —— 其实一点都不复杂，关键是要搞懂每个符号的含义，避免被公式吓住。

3.1 贝叶斯定理的公式

贝叶斯定理的核心公式只有一个：

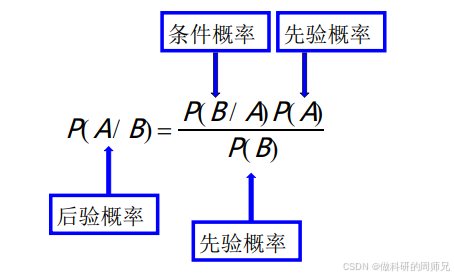
先别急着计算，我们先把每个符号 “翻译” 成通俗的语言，确保入门同学能看懂：

P(A|B)：后验概率（Posterior Probability）—— 这是我们最终要算的 “目标”：在 “事件 B 发生” 的前提下，“事件 A 发生” 的概率。比如 “女神冲我笑（B）” 的前提下，“女神喜欢我（A）” 的概率。
P(A)：先验概率（Prior Probability）—— 在 “没有任何观察结果（比如 B 没发生）” 时，我们对 “事件 A 发生” 的初始判断。比如 “在女神没冲我笑之前，我认为她喜欢我的概率”。
P(B|A)：似然概率（Likelihood）—— 在 “事件 A 已经发生” 的前提下，“事件 B 发生” 的概率。比如 “如果女神喜欢我（A），那么她冲我笑（B）的概率”。
P(B)：证据因子（Evidence）——“事件 B 本身发生” 的总概率，和 A 无关。比如 “不管女神喜不喜欢我，她冲我笑的总概率”。

3.2 核心逻辑：用 “新证据” 更新 “初始判断”

贝叶斯定理的本质，其实是 “用新观察到的证据（B），更新我们对原有事件（A）的初始判断（先验概率 P (A)），最终得到更准确的后验概率（P (A|B)）”。

举个通俗的例子：你一开始觉得 “女神喜欢我” 的概率只有 30%（先验 P (A)=30%）；后来发现 “女神冲我笑了”（新证据 B），而 “女神喜欢一个人时，冲他笑的概率是 40%”（似然 P (B|A)=40%）；再结合 “女神不管喜不喜欢，冲人笑的总概率是 19%”（证据 P (B)=19%）—— 最后算出 “女神冲我笑后，喜欢我的概率是 63.2%”。

这个过程就是 “用新证据更新初始判断”，也是贝叶斯决策论的核心思想。

4. 实例拆解：用贝叶斯定理分析 “女神是否喜欢我”

光看公式和概念还是抽象，我们用一个超贴近生活的实例，一步步计算，帮大家彻底搞懂贝叶斯定理的应用 —— 这也是入门时最容易理解的案例。

4.1 第一步：明确 “目标事件” 和 “观察证据”

首先要把问题转化为 “事件”，避免模糊不清：

目标事件 A：女神喜欢我（这是我们最终想判断的）。
观察证据 B：女神冲我笑（这是我们已经看到的 “事实”）。

我们的目标是计算：P (A|B)—— 女神冲我笑的前提下，她喜欢我的概率。

4.2 第二步：确定 “先验概率 P (A)”

先验概率 P (A) 是 “没有任何证据时，我们对 A 的初始判断”—— 注意：先验概率不是 “瞎猜”，而是基于 “背景信息” 的合理假设。

比如我们通过女神的闺蜜了解到：“女神平时很高冷，很少喜欢别人”—— 基于这个背景，我们合理假设：P (A) = 0.3（即 30%）。

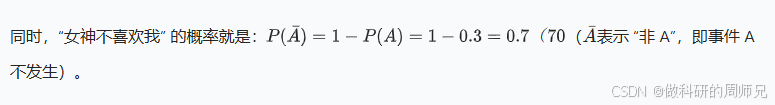
4.5 第五步：代入公式，计算后验概率 P (A|B)

现在我们有了所有需要的数值，直接代入贝叶斯定理公式：

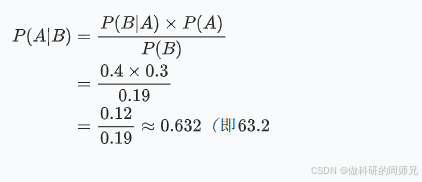
4.6 结果解读：贝叶斯的 “更新” 逻辑

从计算结果能看到：

初始时（没有证据），我们认为女神喜欢我的概率只有 30%（先验 P (A)=30%）；
当观察到 “女神冲我笑”（证据 B）后，这个概率提升到了 63.2%（后验 P (A|B)=63.2%）。

这就是贝叶斯的核心：用新证据不断 “修正” 初始判断，让我们的结论越来越接近真相。

5. 贝叶斯决策论：从 “概率” 到 “决策”

看到这里，可能有同学会问：“我们算出来的是概率，怎么和‘决策论’挂钩？”

其实贝叶斯决策论的逻辑很简单：在分类任务中，我们会计算 “样本属于每个类别的后验概率”，然后选择 “后验概率最大” 的类别作为最终预测结果—— 因为这个选择能最小化 “误判损失”（比如把 “猫” 误判成 “狗” 的损失，比把 “狗” 误判成 “猫” 的损失小，就优先选损失小的）。

举个分类的例子：比如要判断一张图片是 “猫（A1）” 还是 “狗（A2）”，我们会通过贝叶斯定理算出：

P (A1 | 图片) = 70%（图片是猫的概率）；
P (A2 | 图片) = 30%（图片是狗的概率）。

根据贝叶斯决策论，我们会选择 “概率更大的 A1”，即预测这张图片是 “猫”—— 因为这样做，误判的概率最小，损失也最小。

6. 入门启示：贝叶斯决策论的关键注意点

对于刚入门机器学习的同学，学习贝叶斯决策论时，有两个关键点一定要记住，避免误解：

6.1 先验概率不是 “瞎猜”，要基于 “数据 / 背景”

贝叶斯定理中的 “先验概率 P (A)”，不是主观臆断，而是需要基于 “已有数据” 或 “合理背景信息”。比如在 “女神” 案例中，我们的先验 P (A)=30%，是基于 “女神高冷、很少喜欢别人” 的背景；如果没有这个背景，随便设 P (A)=90%，结果就会完全错误。

在实际机器学习中，先验概率通常来自 “历史数据”—— 比如要预测 “用户是否购买商品”，先验概率可以是 “过去 1000 个用户中，有 200 个购买了，所以 P (购买)=20%”。

6.2 贝叶斯是 “动态更新” 的过程

贝叶斯定理不是 “算一次就结束” 的 —— 如果有新的证据出现，我们可以把 “上一次的后验概率” 当成 “新的先验概率”，再次代入公式计算，不断更新判断。

比如 “女神” 案例中，如果后续又观察到 “女神主动和我打招呼（新证据 C）”，我们就可以把之前算的 P (A|B)=63.2% 当成新的先验 P (A)，再结合 “女神喜欢一个人时主动打招呼的概率（P (C|A)）”，算出新的后验概率 P (A|B,C)—— 这样的过程，会让我们的判断越来越准确。