目录
一、基础概念
1.常见名词的含义:
①满二叉树:同时满足如下两个条件的二叉树
1. 要么有两个孩子,要么没有孩子
2. 叶子节点在同一层
满二叉树有如下规律:
如果层数为n
第n层节点数 一定为 2^(n-1)
整颗树节点数 为 2^n - 1
②完全二叉树满二叉树 从 下边 右边开始删节点
从右往左 从下往上 (和 阅读顺序 相反)
满二叉树一定是完全二叉树
完全二叉树不一定是满二叉树③堆:有序的完全二叉树
仅在父子之间有序 兄弟之间 其他节点之间 不管
父大于子:最大堆 (大顶堆)
父小于子:最小堆 (小顶堆)2.在数组中表现出的规律:
①已知父节点下标为N
左孩子下标为:2*N + 1
右孩子下标为:2*N + 2②已知左孩子下标为M 父节点下标为: (M-1)/2
已知右孩子下标为M 父节点下标为: (M-2)/2=>(整除的性质)合并为:已知孩子下标为M 父下标为: (M-1)/2
二、代码实现:
1.框架
主要是实现堆的:
①堆的元素插入②堆用指定数组初始化③删除堆顶元素④删除指定元素⑤堆排序
template<class T> class MyHeap//写一个大顶堆 { public: MyHeap() { pRoot = nullptr; len = MaxLen = 0; } ~MyHeap() { if (pRoot)delete pRoot; pRoot = nullptr; len = MaxLen = 0; } void travel() { for (int i = 0; i < len; i++) { cout << pRoot[i] << " "; }cout << endl; } void swap(T& a, T& b); void push(const T& data); void init(T* pArr, int n); T pop(); void deleteNode(const T& data); private: T* pRoot; size_t len; size_t MaxLen; }; template<class T> inline void MyHeap<T>::swap(T& a, T& b) { T temp=a; a = b; b = temp; }
2.插入push:
思路:将新元素放到最后一个位置,然后向上浮动(adjust)
这里提供了两种写法:
①交换的方法:简单一些,只不过需要单独写一个swap
②覆盖:优化交换的写法,只不过终止条件参数的比较的时候,用的是第一次被覆盖的元素
template<class T> inline void MyHeap<T>::push(const T& data) { //step1:先把数据放进来 if (MaxLen <= len) { MaxLen += ((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1; T* pNew = new T[MaxLen]; if (pRoot)//不为空的时候才需要进行拷贝+delete { memcpy(pNew, pRoot, sizeof(T) * len); delete pRoot; } pRoot = pNew; } pRoot[len++] = data;//先把数据放进来 //step2:堆调整 size_t CurrentIdx = len-1; size_t ParentIdx = (CurrentIdx - 1) / 2; #if 0 //覆盖写法!!!->注意终止条件 while (1) { if (CurrentIdx <= 0)break;//终止情况一:没有父节点 ParentIdx = (CurrentIdx - 1) / 2; if (data< pRoot[ParentIdx])break;//终止情况二:已经符合大顶堆的要求(父大于子) pRoot[CurrentIdx] = pRoot[ParentIdx]; CurrentIdx = ParentIdx;//向上切换 } pRoot[CurrentIdx] = data; #else if //swap写法 while (1) { if (CurrentIdx <= 0)break;//终止情况一:没有父节点 ParentIdx = (CurrentIdx - 1) / 2; if (data < pRoot[ParentIdx])break;//终止情况二:已经符合大顶堆的要求(父大于子) swap(pRoot[CurrentIdx],pRoot[ParentIdx]); CurrentIdx = ParentIdx;//向上切换 } #endif }
3.指定数组构建堆init
本处采用的是覆盖的写法(包括下面的所有写法)
template<class T> inline void MyHeap<T>::init(T* pArr, int n) { assert(pArr);//防止为nullptr //step1:先把数据放进来 for (int i=0;i<n;i++) { if (MaxLen <= len) { MaxLen += ((MaxLen >> 1) > 1) ? (MaxLen >> 1) : 1; T* pNew = new T[MaxLen]; if (pRoot)//不为空的时候才需要进行拷贝+delete { memcpy(pNew, pRoot, sizeof(T) * len); delete pRoot; } pRoot = pNew; } pRoot[len++] = pArr[i];//先把数据放进来 //step2:堆调整 size_t CurrentIdx = len - 1; size_t ParentIdx = (CurrentIdx - 1) / 2; //覆盖写法!!!->注意终止条件 while (1) { if (CurrentIdx <= 0)break;//终止情况一:没有父节点 ParentIdx = (CurrentIdx - 1) / 2; if (pArr[i] < pRoot[ParentIdx])break;//终止情况二:已经符合大顶堆的要求(父大于子) pRoot[CurrentIdx] = pRoot[ParentIdx]; CurrentIdx = ParentIdx;//向上切换 } pRoot[CurrentIdx] = pArr[i]; } }
4.删除堆顶元素 pop():
思路:将数组最后一个元素覆盖掉堆顶元素,由于其他位置均有序(父子间),所以只需要调整一次堆!
template<class T> inline T MyHeap<T>::pop() { if (len == 0) { cout << "堆空,删除失败" << endl; return T(-1); } if (len == 1) { T temp = pRoot[len - 1]; len--; return temp; } //step1:临时保存堆顶元素 T temp = pRoot[0]; //step2:将最后一个元素覆盖堆顶元素 pRoot[0] = pRoot[len - 1]; //step3:调整堆 int CurrentIdx = 0; int PriChildIdx=(2*CurrentIdx)+1;//两个孩子中较小的那个孩子,先假定是左孩子较大 //....需要找到较大的那个孩子,和父节点比较 #if 0 while (1) { if ((2 * CurrentIdx) + 1 > len - 1)break;//说明当前点没有左右孩子 PriChildIdx = (2 * CurrentIdx) + 1; if ((2 * CurrentIdx) + 2 <= len - 1&&pRoot[PriChildIdx] < pRoot[PriChildIdx + 1]) ++PriChildIdx;//找出最大的孩子(前提是有右孩子) if (pRoot[len-1] > pRoot[PriChildIdx])break;//说明已经符合大顶堆的条件了(注意:这边用的覆盖->注意比较的终止条件是pRoot[len-1]) pRoot[CurrentIdx] = pRoot[PriChildIdx]; CurrentIdx = PriChildIdx;//切换到下一层 } pRoot[CurrentIdx] = pRoot[len - 1]; len--; #else if while (1) { if ((2 * CurrentIdx + 1 > len - 1))break; PriChildIdx = (2 * CurrentIdx) + 1; if ((2 * CurrentIdx) + 2 <= len - 1 && pRoot[PriChildIdx] < pRoot[PriChildIdx + 1]) ++PriChildIdx;//找出最大的孩子(前提是有右孩子) if (pRoot[len - 1] > pRoot[PriChildIdx])break;//说明已经符合大顶堆的条件了(注意:这边用的覆盖->注意比较的终止条件是pRoot[len-1]) swap(pRoot[CurrentIdx],pRoot[PriChildIdx]); CurrentIdx = PriChildIdx;//切换到下一层 } len--; #endif return temp; }
5.指定元素的删除
现在数组中找到这个元素pdel,然后用数组最后一个元素覆盖pdel的位置
①若pdel的父值大于pdel(符合大顶堆),所以应该向下调整
②若pdel>pdel的父,那么下面一定是有序的,所以应该向上调整一次即可。
template<class T> inline void MyHeap<T>::deleteNode(const T& data) { //step1:找出位置并用最后一个元素覆盖 int CurrentIdx = 0; for (CurrentIdx = 0; CurrentIdx < len; CurrentIdx++) { if (pRoot[CurrentIdx] == data)break; }//得到需要调整元素的下标 if (CurrentIdx >= len)return; int FatherIdx = (CurrentIdx - 1) / 2;//求出父节点 //step2:堆调整 if (CurrentIdx == 0)//删除堆顶元素 { pop(); return; } else if (pRoot[FatherIdx] > pRoot[CurrentIdx])//上面父节点之间已经有序->向下进行调整 { pRoot[CurrentIdx] = pRoot[len - 1];//覆盖 int PriChildIdx = 2 * CurrentIdx + 1;//假定最大子孩是左子孩 while (1) { PriChildIdx = 2 * CurrentIdx + 1;//假定最大子孩是左子孩 if (PriChildIdx > len - 1)break;//无左右子孩 if ((PriChildIdx + 1) <= len - 1 && pRoot[PriChildIdx] < pRoot[PriChildIdx + 1])//前提有右子孩->找出较大的子孩 PriChildIdx++; if (pRoot[PriChildIdx] < pRoot[len-1])break;//满足大顶堆 pRoot[CurrentIdx] = pRoot[PriChildIdx]; CurrentIdx = PriChildIdx;//切换 } } else//既然当前节点比父节点要大,而父节点必定比当前节点的孩子节点要大->需要向上调整 { pRoot[CurrentIdx] = pRoot[len - 1];//覆盖 while (1) { if (CurrentIdx <= 0)break;//无父节点 FatherIdx= (CurrentIdx - 1) / 2;//求出父节点 if (pRoot[FatherIdx] > pRoot[len-1])break;//已经符合 pRoot[CurrentIdx] = pRoot[FatherIdx]; CurrentIdx = FatherIdx;//切换 } } pRoot[CurrentIdx] = pRoot[len - 1]; len--; }
6.堆排序
堆排序算法大概就分为两个步骤:
- 构造堆(调整数组,使其满足最大堆或最小堆)
- 排序
template<class T> void Swap(T& a, T& b) { T t = a; a = b; b = t; } template<class T> void Greater_heap(T a[], int start, int end)//将数组a变成(单次)一个大顶堆(start和end分别是a的起止下标,闭区间 { int CurrentIdx = start; int PriChildIdx = 2 * CurrentIdx + 1;//先默认左孩子是较大的 T temp = a[CurrentIdx]; while (1) { if (2 * CurrentIdx + 1 > end)break;//无左右孩子 int PriChildIdx = 2 * CurrentIdx + 1;//先默认左孩子是较大的 if (PriChildIdx + 1 <= end && a[PriChildIdx] < a[PriChildIdx + 1])++PriChildIdx;//选出较大的孩子 if (a[PriChildIdx] < temp)break;//符合要求,break a[CurrentIdx] = a[PriChildIdx]; CurrentIdx = PriChildIdx; } a[CurrentIdx] = temp; } template<class T> void HeapSort(T a[],int length) { assert(a);//防止为nullptr for (int i = (length/2-1); i >=0; i--) {//(length/2-1)是最后一个父节点的下标,通过这个for循环,将数组堆化(从第一个分堆逐一构建) Greater_heap(a, i, length-1); } for (int i = 0; i <length-1; i++)//挑n-1次即可 { Swap(a[0], a[length - 1-i]); Greater_heap(a, 0, length - i - 2); } }
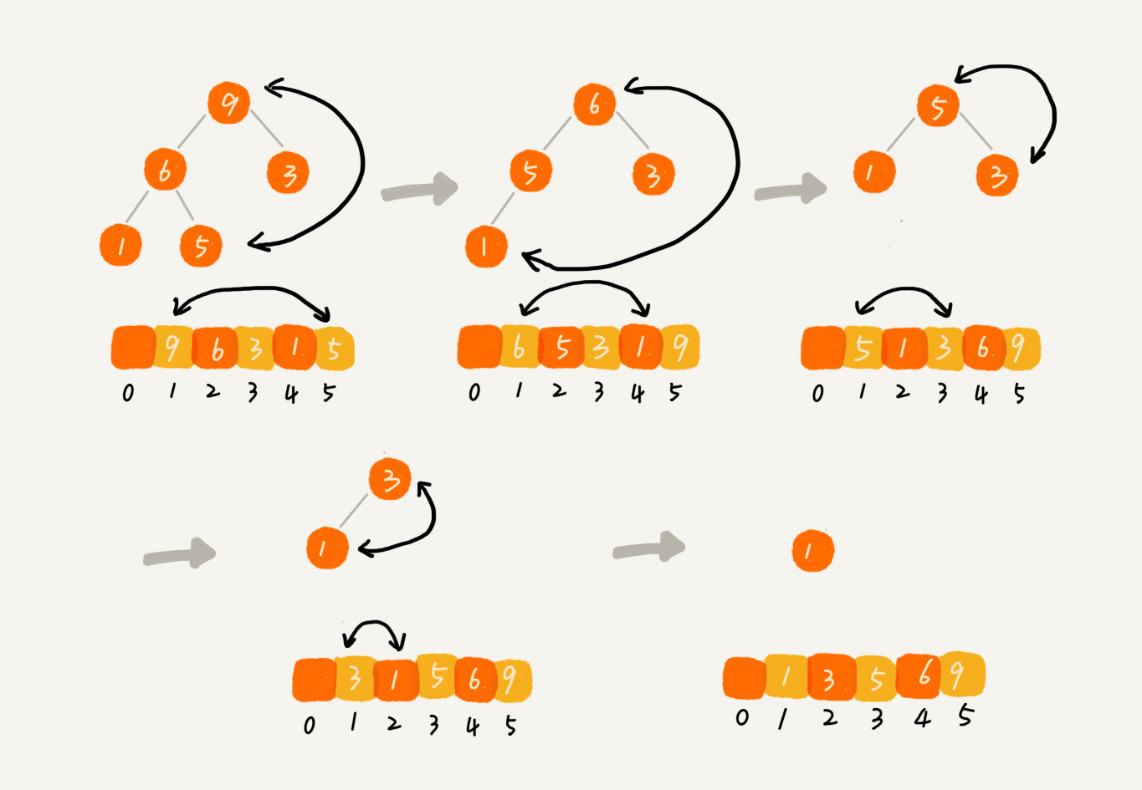
注意:此处涉及到最后一个父节点的下标(length/2-1)
三、堆的应用:
1.优先级队列:
很多数据结构和算法都要依赖它。比如,赫夫曼编码、图的最短路径、最小生成树算法等等。不仅如此,很多语言中,都提供了优先级队列的实现,比如,Java的PriorityQueue,C++的priority_queue等。
①合并有序小文件
假设我们有100个小文件,每个文件的大小是100MB,每个文件中存储的都是有序的字符串。我们希望将这些100个小文件合并成一个有序的大文件。这里就会用到优先级队列
这里就可以用到优先级队列,也可以说是堆。我们将从小文件中取出来的字符串放入到小顶堆中,那堆顶的元素,也就是优先级队列队首的元素,就是最小的字符串。我们将这个字符串放入到大文件中,并将其从堆中删除。然后再从小文件中取出下一个字符串,放入到堆中。循环这个过程,就可以将100个小文件中的数据依次放入到大文件中。
我们知道,删除堆顶数据和往堆中插入数据的时间复杂度都是O(logn),n表示堆中的数据个数,这里就是100。是不是比原来数组存储的方式高效了很多呢?
② 高性能定时器
假设我们有一个定时器,定时器中维护了很多定时任务,每个任务都设定了一个要触发执行的时间点。定时器每过一个很小的单位时间(比如1秒),就扫描一遍任务,看是否有任务到达设定的执行时间。如果到达了,就拿出来执行。
但是,这样每过1秒就扫描一遍任务列表的做法比较低效,主要原因有两点:第一,任务的约定执行时间离当前时间可能还有很久,这样前面很多次扫描其实都是徒劳的;第二,每次都要扫描整个任务列表,如果任务列表很大的话,势必会比较耗时。
针对这些问题,我们就可以用优先级队列来解决。我们按照任务设定的执行时间,将这些任务存储在优先级队列中,队列首部(也就是小顶堆的堆顶)存储的是最先执行的任务。
这样,定时器就不需要每隔1秒就扫描一遍任务列表了。它拿队首任务的执行时间点,与当前时间点相减,得到一个时间间隔T。
这个时间间隔T就是,从当前时间开始,需要等待多久,才会有第一个任务需要被执行。这样,定时器就可以设定在T秒之后,再来执行任务。从当前时间点到(T-1)秒这段时间里,定时器都不需要做任何事情。
当T秒时间过去之后,定时器取优先级队列中队首的任务执行。然后再计算新的队首任务的执行时间点与当前时间点的差值,把这个值作为定时器执行下一个任务需要等待的时间。
这样,定时器既不用间隔1秒就轮询一次,也不用遍历整个任务列表,性能也就提高了。
2.利用堆求Top K
求Top K的问题抽象成两类:
①一类是针对静态数据集合,也就是说数据集合事先确定,不会再变。
针对静态数据,如何在一个包含n个数据的数组中,(目标)查找前K大数据呢?我们可以维护一个大小为K的小顶堆,顺序遍历数组,从数组中取出取数据与堆顶元素比较。如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;如果比堆顶元素小,则不做处理,继续遍历数组。这样等数组中的数据都遍历完之后,堆中的数据就是前K大数据了。
遍历数组需要O(n)的时间复杂度,一次堆化操作需要O(logK)的时间复杂度,所以最坏情况下,n个元素都入堆一次,所以时间复杂度就是O(nlogK)。
②另一类是针对动态数据集合,也就是说数据集合事先并不确定,有数据动态地加入到集合中。
针对动态数据求得Top K就是实时Top K。怎么理解呢?我举一个例子。一个数据集合中有两个操作,一个是添加数据,另一个询问当前的前K大数据。
如果每次询问前K大数据,我们都基于当前的数据重新计算的话,那时间复杂度就是O(nlogK),n表示当前的数据的大小。实际上,我们可以一直都维护一个K大小的小顶堆,当有数据被添加到集合中时,我们就拿它与堆顶的元素对比。如果比堆顶元素大,我们就把堆顶元素删除,并且将这个元素插入到堆中;如果比堆顶元素小,则不做处理。这样,无论任何时候需要查询当前的前K大数据,我们都可以里立刻返回给他。













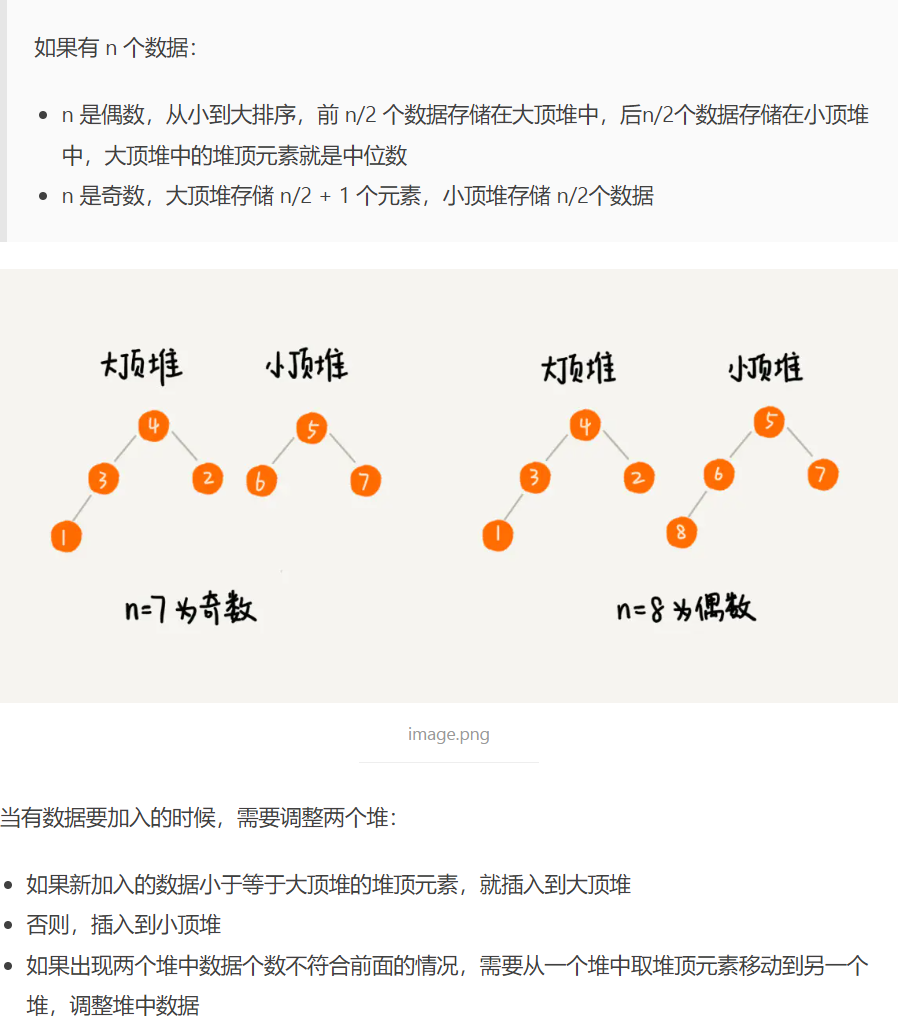
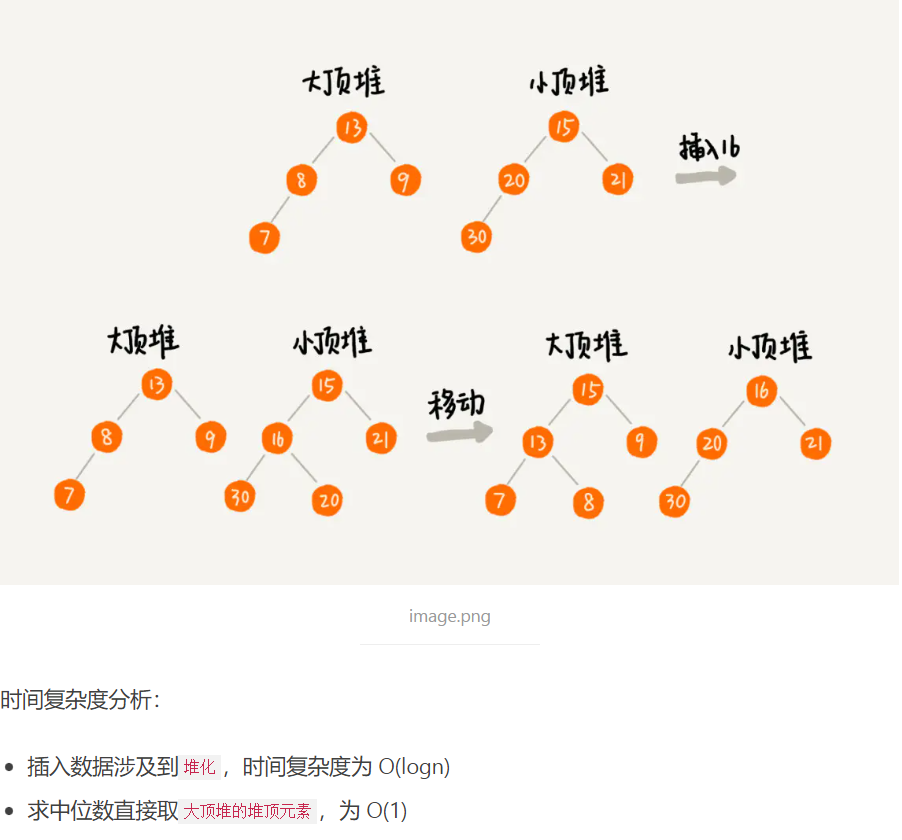
















 3019
3019











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










