关于平衡树的一些学习

最新推荐文章于 2021-04-13 11:08:31 发布

zjq_01

最新推荐文章于 2021-04-13 11:08:31 发布

阅读量444

点赞数

分类专栏：平衡树数据结构学习笔记文章标签：学习笔记平衡树

本文链接：https://blog.csdn.net/zjq_01/article/details/72934851

版权

学习笔记同时被 3 个专栏收录

5 篇文章 0 订阅

订阅专栏

数据结构

4 篇文章 0 订阅

订阅专栏

平衡树

1 篇文章 0 订阅

订阅专栏

听说平衡树种类很多，什么RBT，AVL，BST，Splay~~，跳表~~什么的，简单谈一谈。

（1）红黑树又叫RBT ，实现复杂性能强悍，在OI中较少出现QAQ

（2）Splay 第一个接触的平衡树，一开始还以为Splay是唯一的平衡树~~(我是SB）~~，splay的原理是：每插入一个点，就把它旋转到根节点，Splay不能保证每次旋转操作的复杂度的是O（log(n)），但是它的均摊复杂度确实是log(n)，~~证明我也不会~~，听说splay会被卡，等到被卡了再说吧QAQ，编程复杂度也小，Splay的核心在于splay操作即是Splay（x，f）把x旋转到f的儿子上，特别的如果要旋转到根，那么f=0 Splay的旋转操作分为zig，zig-zig，zig-zag。

zig操作：当x的父亲已经是f的儿子时，直接旋转x。

zig-zig操作：当x与x的父亲位于同一侧时，即x是x的父亲的左儿子，x的父亲是x的父亲的父亲的左儿子，反之也成立。

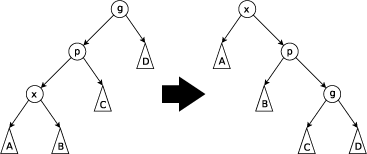
zig-zag操作：当x与x的父亲位于不同侧时，直接旋转两次x。这里的旋转，就是指，如果x是它父亲的左儿子，那么就把他右旋，否则左旋。如图

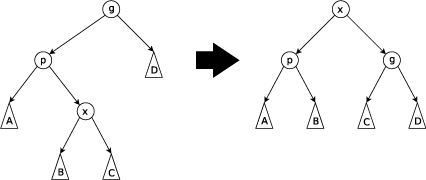
Splay Tree可以方便的解决一些区间问题，根据不同形状二叉树先序遍历结果不变的特性，可以将区间按顺序建二叉查找树。

每次自下而上的一套splay都可以将x移动到根节点的位置，利用这个特性，可以方便的利用Lazy的思想进行区间操作。

对于每个节点记录size，代表子树中节点的数目，这样就可以很方便地查找区间中的第k小或第k大元素。

对于一段要处理的区间[x, y]，首先splay x-1到root，再splay y+1到root的右孩子，这时root的右孩子的左孩子对应子树就是整个区间。————————从别的地方抄来的

贴上代码：

int father[N],key[N],ch[N][2],root,tot1;  //分别表示父结点，键值，左右孩子(0为左孩子，1为右孩子),根结点，结点数量 
void Rotate(int x,int kind) {  
    int y=father[x];  
    //把其中一个分支先给父节点   
    ch[y][!kind]=ch[x][kind];  
    father[ch[x][kind]]=y;  
    //如果父节点不是根结点，则要和父节点的父节点连接起来    
    if(father[y])  
        ch[father[y]][ch[father[y]][1]==y]=x;  
    father[x]=father[y];  
    ch[x][kind]=y;  
    father[y]=x;  
}  
//Splay调整，将根为r的子树调整为goal    
void Splay(int r,int goal) {  
    while(father[r]!=goal) {  
    //父节点即是目标位置，goal为0表示，父节点就是根结点    
        if(father[father[r]]==goal)  
            Rotate(r,ch[father[r]][0]==r);  
        else {  
            int y=father[r];  
            int kind=ch[father[y]][0]==y;  
            //两个方向不同，则先左旋再右旋    
            if(ch[y][kind]==r) {  
                Rotate(r,!kind);  
                Rotate(r,kind);  
            }  
            //两个方向相同，相同方向连续两次     
            else {  
                Rotate(y,kind);  
                Rotate(r,kind);  
            }  
        }  
    }  
    //更新根结点    
    if(goal==0) root=r;  
}

二. Treap

我来填坑了，先给一道模板题 BZOJ3224 普通平衡树可以用Treap做

一些定义如下

#include<bits/stdc++.h>
using namespace std;
struct data  
{  
    int l , r , v , rnd , size , w ;  
};  
data tr[100001] ;  
int n , ans , size , root ;  
void update(int k)  
{  
    tr[k].size = tr[tr[k].l].size + tr[tr[k].r].size + tr[k].w ;  
}  
void lturn(int &k)  
{  
    int t = tr[k].r ;  
    tr[k].r = tr[t].l ;  
    tr[t].l = k ;  
    tr[t].size = tr[k].size ;  
    update(k) ;  
    k = t ;  
}  
void rturn(int &k)  
{  
    int t = tr[k].l ;  
    tr[k].l = tr[t].r ;  
    tr[t].r = k ;  
    tr[t].size = tr[k].size ;  
    update(k) ;  
    k = t ;  
}

左旋和右旋看着图理解一下吧，实在不行记住代码也行QAQ

插入代码：

void insert(int &k , int x)  
{  
    if(k == 0)  
    {  
        size ++ ;  
        k = size ;  
        tr[k].size = tr[k].w = 1 ;  
        tr[k].v = x ;  
        tr[k].rnd = rand() ;  
        return ;  
    }  
    tr[k].size ++ ;  
    if(tr[k].v == x) tr[k].w ++ ;  
    else if(x > tr[k].v)  
    {  
        insert(tr[k].r , x) ;  
        if(tr[tr[k].r].rnd < tr[k].rnd) lturn(k) ;  
    }else   
    {  
        insert(tr[k].l , x) ;  
        if(tr[tr[k].l].rnd < tr[k].rnd) rturn(k) ;  
    }  
}

1.先讨论没有节点的情况，那就新加入一个节点

2.若当前节点的权值与插入的值相同，那么给当前节点w+1

3.与当前节点权值作比较，如果插入值大于当前节点权值则插入到右边，反之插入到左边，同时维护小根堆的特点

删除操作：

void del(int &k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v == x)  
    {  
        if(tr[k].w > 1)  
        {  
            tr[k].w -- , tr[k].size -- ;  
            return ;  
        }  
        if(tr[k].l * tr[k].r == 0) k = tr[k].l + tr[k].r ;  
        else if(tr[tr[k].l].rnd < tr[tr[k].r].rnd)  
        {  
            rturn(k) ;  
            del(k , x) ;  
        }else  
        {  
            lturn(k) ;  
            del(k , x) ;  
        }  
    }else if(x > tr[k].v)  
    {  
        tr[k].size -- ;  
        del(tr[k].r , x) ;  
    }else  
    {  
        tr[k].size -- ;  
        del(tr[k].l , x) ;  
    }  
}

1.没有节点不删除

2.删除值与当前节点的值相同且当前节点的值的个数大于1则减一

3.若k处只有一个子节点，则把子节点提上来

4.如果左边rnd小于右边rnd，则右旋，把这个根节点旋到叶节点处删掉

4.如果右边rnd小于左边rnd，则左旋，把这个根节点旋到叶节点处删掉

5.如果比k处的值大，则将k的size--然后分到右子树操作

5.如果比k处的值小，则将k的size--然后分到左子树操作

查询排名操作：

int query_rank(int k , int x)  
{  
    if(k == 0) return 0 ;  
    if(tr[k].v == x) return tr[tr[k].l].size + 1 ;  
    else if(x > tr[k].v)  
    {  
        return tr[tr[k].l].size + tr[k].w + query_rank(tr[k].r , x) ;  
    }else return query_rank(tr[k].l , x) ;  
}

1.讨论没有节点的情况

2.若当前节点的值与查询值相同，则返回左子树的节点数+1；

3.若当前节点的值小于被查询的值，则返回左子树的节点数+当前节点的数目+查询到右子树的返回值

4.若当前节点的值大于被查询的值，则返回查询到左子树的返回值

查询排名为x的数的操作：

int query_num(int k , int x)  
{  
    if(k == 0) return 0 ;  
    if(x <= tr[tr[k].l].size)  
    {  
        return query_num(tr[k].l , x) ;  
    }else if(x > tr[tr[k].l].size + tr[k].w)  
    {  
        return query_num(tr[k].r , x - tr[tr[k].l].size - tr[k].w) ;  
    }else  
    {  
        return tr[k].v ;  
    }  
}

1.讨论没有节点的情况

2.如果x小于等于左子树的节点数则递归询问

3.如果x比左子树的节点数加k处节点数还大，则返回对右子树的x-左子树节点数-k处节点数的递归询问。

4.除了2,3情况就一定是k处，返回k处的值就好了

求前驱：

前驱定义：该节点的前一个节点

void query_pro(int k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v < x)  
    {  
        ans = k ;  
        query_pro(tr[k].r , x) ;  
    }else query_pro(tr[k].l , x) ;  
}

1.讨论没有节点的情况

2.如果x比k处的值大，则用ans记录k，然后递归到右子树

3.如果k处的值大于等于x，则递归到左子树

求后继：

后继定义：该节点的后一个节点

void query_sub(int k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v > x)  
    {  
        ans = k ;  
        query_sub(tr[k].l , x) ;  
    }else query_sub(tr[k].r , x) ;  
}

1.讨论没有节点的情况

2.如果x比k处的值小，则用ans记录k，然后递归到左子树

3.如果k处的值大于等于x，则递归到右子树

基本操作已经叙述完了，下面贴上主函数，大家就可以去把上面那到题水掉了QAQ

贴上全代码：

#include<bits/stdc++.h>
using namespace std;
struct data  
{  
    int l , r , v , rnd , size , w ;  
};  
data tr[100001] ;  
int n , ans , size , root ;  
void update(int k)  
{  
    tr[k].size = tr[tr[k].l].size + tr[tr[k].r].size + tr[k].w ;  
}  
void lturn(int &k)  
{  
    int t = tr[k].r ;  
    tr[k].r = tr[t].l ;  
    tr[t].l = k ;  
    tr[t].size = tr[k].size ;  
    update(k) ;  
    k = t ;  
}  
void rturn(int &k)  
{  
    int t = tr[k].l ;  
    tr[k].l = tr[t].r ;  
    tr[t].r = k ;  
    tr[t].size = tr[k].size ;  
    update(k) ;  
    k = t ;  
}
void insert(int &k , int x)  
{  
    if(k == 0)  
    {  
        size ++ ;  
        k = size ;  
        tr[k].size = tr[k].w = 1 ;  
        tr[k].v = x ;  
        tr[k].rnd = rand() ;  
        return ;  
    }  
    tr[k].size ++ ;  
    if(tr[k].v == x) tr[k].w ++ ;  
    else if(x > tr[k].v)  
    {  
        insert(tr[k].r , x) ;  
        if(tr[tr[k].r].rnd < tr[k].rnd) lturn(k) ;  
    }else   
    {  
        insert(tr[k].l , x) ;  
        if(tr[tr[k].l].rnd < tr[k].rnd) rturn(k) ;  
    }  
} 
void del(int &k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v == x)  
    {  
        if(tr[k].w > 1)  
        {  
            tr[k].w -- , tr[k].size -- ;  
            return ;  
        }  
        if(tr[k].l * tr[k].r == 0) k = tr[k].l + tr[k].r ;  
        else if(tr[tr[k].l].rnd < tr[tr[k].r].rnd)  
        {  
            rturn(k) ;  
            del(k , x) ;  
        }else  
        {  
            lturn(k) ;  
            del(k , x) ;  
        }  
    }else if(x > tr[k].v)  
    {  
        tr[k].size -- ;  
        del(tr[k].r , x) ;  
    }else  
    {  
        tr[k].size -- ;  
        del(tr[k].l , x) ;  
    }  
}  
int query_rank(int k , int x)  
{  
    if(k == 0) return 0 ;  
    if(tr[k].v == x) return tr[tr[k].l].size + 1 ;  
    else if(x > tr[k].v)  
    {  
        return tr[tr[k].l].size + tr[k].w + query_rank(tr[k].r , x) ;  
    }else return query_rank(tr[k].l , x) ;  
} 
int query_num(int k , int x)  
{  
    if(k == 0) return 0 ;  
    if(x <= tr[tr[k].l].size)  
    {  
        return query_num(tr[k].l , x) ;  
    }else if(x > tr[tr[k].l].size + tr[k].w)  
    {  
        return query_num(tr[k].r , x - tr[tr[k].l].size - tr[k].w) ;  
    }else  
    {  
        return tr[k].v ;  
    }  
}
void query_pro(int k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v < x)  
    {  
        ans = k ;  
        query_pro(tr[k].r , x) ;  
    }else query_pro(tr[k].l , x) ;  
}
void query_sub(int k , int x)  
{  
    if(k == 0) return ;  
    if(tr[k].v > x)  
    {  
        ans = k ;  
        query_sub(tr[k].l , x) ;  
    }else query_sub(tr[k].r , x) ;  
} 
int main()  
{  
    scanf("%d" , &n) ;  
    int opt , x ;  
    for(int i = 1 ; i <= n ; i++)  
    {  
        scanf("%d%d" , &opt , &x) ;  
        switch(opt)  
        {  
            case 1 :insert(root , x) ;break ;  
            case 2 :del(root , x) ;break ;  
            case 3 :printf("%d\n" , query_rank(root , x)) ;break ;  
            case 4 :printf("%d\n" , query_num(root , x)) ;break ;  
            case 5 :ans = 0;query_pro(root , x);printf("%d\n" , tr[ans].v);break ;  
            case 6 :ans = 0;query_sub(root , x);printf("%d\n" , tr[ans].v);break ;  
        }  
    }  
}

三.SBT

挖坑待填

四.替罪羊树

什么都不会，挖坑待填QAQ