Given an m x n matrix of positive integers representing the height of each unit cell in a 2D elevation map, compute the volume of water it is able to trap after raining.
Note:
Both m and n are less than 110. The height of each unit cell is greater than 0 and is less than 20,000.
Example:
Given the following 3x6 height map: [ [1,4,3,1,3,2], [3,2,1,3,2,4], [2,3,3,2,3,1] ] Return 4.
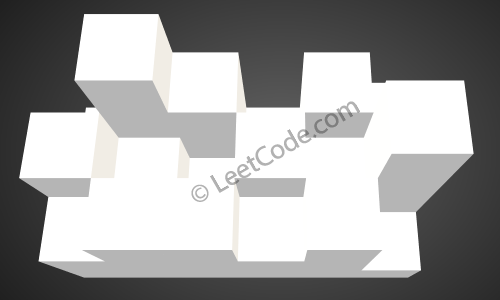
The above image represents the elevation map [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]] before the rain.
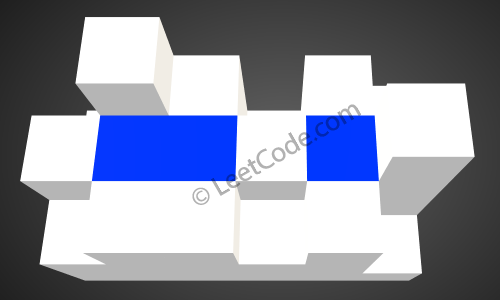
After the rain, water is trapped between the blocks. The total volume of water trapped is 4.
思路:从外向里遍历,因为是是从外面包住里面;
木桶理论,总的来说思路类似于1维情况下的2 pointer解法
import heapq
class Solution:
def trapRainWater(self, a):
"""
:type heightMap: List[List[int]]
:rtype: int
"""
if not a or not a[0]: return 0
n,m=len(a),len(a[0])
if n<=2 or m<=2: return 0
q = []
d=[[0,1],[0,-1],[1,0],[-1,0]]
marked = [[False for _ in range(m)] for _ in range(n)]
res = 0
for i in range(m):
heapq.heappush(q, (a[0][i],0,i))
heapq.heappush(q, (a[n-1][i],n-1,i))
marked[0][i]=marked[n-1][i]=True
for i in range(1,n-1):
heapq.heappush(q, (a[i][0],i,0))
heapq.heappush(q, (a[i][m-1],i,m-1))
marked[i][0]=marked[i][m-1]=True
while q:
h,i,j=heapq.heappop(q)
for di,dj in d:
ii,jj=i+di,j+dj
if 0<=ii<n and 0<=jj<m and not marked[ii][jj]:
heapq.heappush(q, (max(a[ii][jj], h),ii,jj))
marked[ii][jj] = True
res += max(0, h-a[ii][jj])
return res
s=Solution()
print(s.trapRainWater([
[1,4,3,1,3,2],
[3,2,1,3,2,4],
[2,3,3,2,3,1]
]))
























 635
635

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








