高斯素数判定

zmlbsdd

已于 2023-10-30 13:28:38 修改

阅读量758

点赞数 3

文章标签：线性代数抽象代数几何学

于 2023-07-23 15:45:17 首次发布

本文链接：https://blog.csdn.net/zml19136706515/article/details/131880097

版权

高斯素数及其判定方法

一、复数相关概念

1、定义：

复数通常写为如下形式：

$z = a + bi$ ,

其中 a 和 b 是实数，a 称为复数的实部， b 称为复数的虚部，实数可以看为虚部为0的复数，对于实部为0而虚部不为0的复数称为纯虚数。

2 复平面：

以纵轴为虚轴（对应一个复数的虚部），横轴为实轴（对应实部）建立平面直角坐标系，那么任意一个复数都可以表示为复平面上的一个点，同样，复平面上的一个点也对应一个复数。

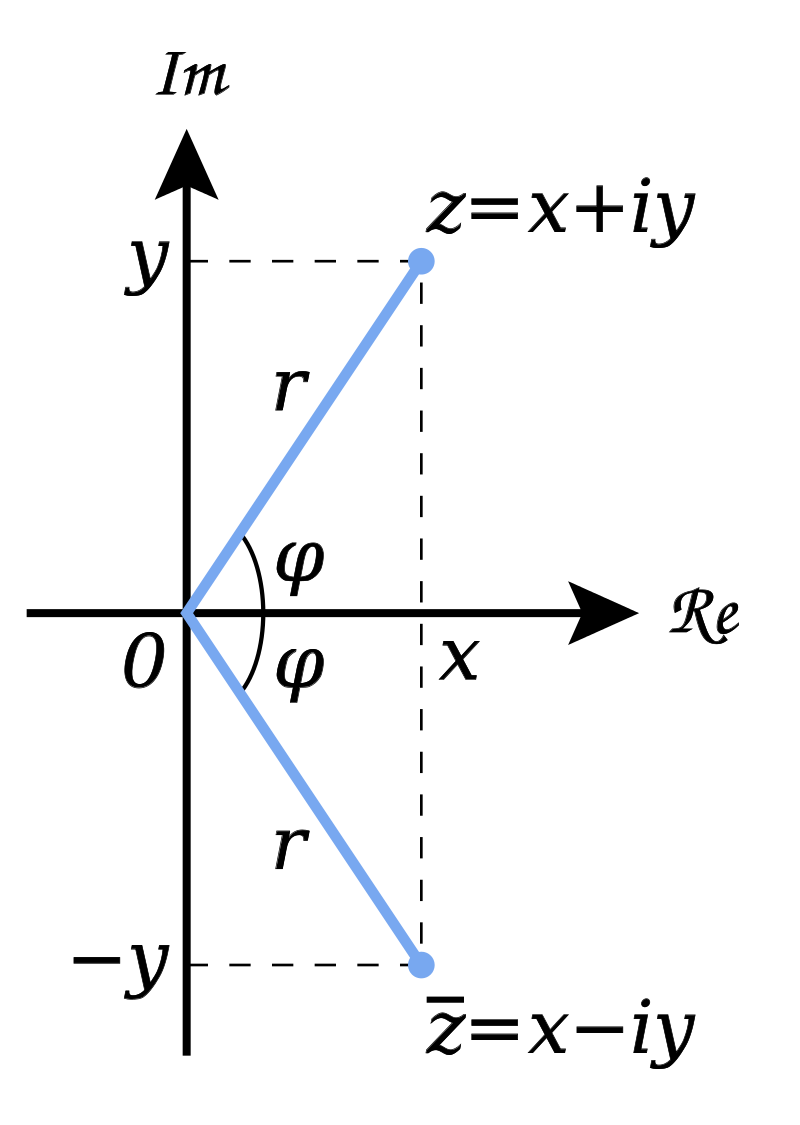
3、共轭：

（1）定义：

对于复数 $z = a + bi$ ,定义 $z$ 的共轭为 $\bar z = a - bi$ .

（2）性质：

$\overline{z+w}=\bar z + \bar w$
$\overline{zw}=\bar z \bar w$
$\left |\frac{z}{w} \right |$ = $\frac{\left | z \right |}{\left | w \right |}$

4、计算：

设 $z_1 = a_1 + b_1i$ ， $z_2 = a_2 + b_2i$ ,则：

$z_1 \pm z_2 = (a_1 \pm a_2) + (b_1 \pm b_2)i$ , 在复平面中表示两个向量相加减。
$z_1 \times z_2 = (a_1 \times a_2 - b_1 \times b_2) + (a_1 \times b_2 + a_2 \times b_1)i$ , 在平面中， $z_1z_2$ 的结果代表的向量为 $z_1，z_2$ 所代表的向量模长相乘，相角相加后得到的向量。
$z_1 \div z_2 = \frac{z_1 \times \bar z_2 }{z_2 \times \bar z_2}$ ,除法在复平面代表的含义与乘法恰好相反

5、模、范数：

对于复数 z = a + bi , 定义 z 的模|z|为： $\left | z \right | = \sqrt{a^2+b^2}$

对于复数 z = a + bi , 定义 z 的范数 $N (z)$ 为: $\times$ $\bar z$

6、范数的性质（重点）： $N(z_1z_2) = N(z_1)N(z_2)$

证明：

$设 z_1 = a_1 + b_1i ,z_2 = a_2 + b_2i$
$z_1 \times z_2 = (a_1a_2 + i^2 b_1b_2) + (a_1b_2 + a_2b_1)i$
$\therefore N(z_1z_2)\\=(a_1a_2+i^2b_1b_2)^2-(a_1b_2+a_2b_1)^2i^2$ $a_1^2a_2^2-i^2a_1^2b_2^2-i^2a_2^2b_1^2-i^4b_1^2b_2^2$
$\because N(z_1) = a_1^2 - b_1^2 *i^2 ,N(z_2)=a_2^2 - b_2^2 i^2$
$\therefore N(z_1)N(z_2)= a_1^2a_2^2-i^2a_1^2b_2^2-i^2a_2^2b_1^2-i^4b_1^2b_2^2$
$\therefore N(z_1z_2)=N(z_1)N(z_2)$

$i=\sqrt{-1}成立,对于\sqrt{-2}、\sqrt{-3}......\sqrt{-n}也是成立的$ .

二、高斯整数

1、定义：

实部和虚部都为实整数的复数，称为高斯整数，比如： $2 + 3 i, 1 + 2 i$ 等等，对应着复平面上的整点。

（若将 $i=\sqrt{-1}$ ,替换为 $i=\sqrt{-k}$ ，这样的数也叫高斯整数，但不一定满足整数唯一分解定理，现如今数学家们已经证明当且仅当 $k = 1, 2, 3, 7, 11, 19, 67, 163$ 时整数唯一分解定理成立）

2、高斯整数中的单位：

对于一个高斯整数 $\varepsilon$ ,若 $N(\varepsilon )=1$ ,则称 $\varepsilon$ 为单位 ( 相当于整数中的1 )，显然，对于 $i=\sqrt{-1}$ 的情况，单位只有： $\pm1,\pm i$

3、相伴：

$\varepsilon z$ 称为 $z$ 的相伴.

4、整除：

对于高斯整数 $z$ ,若存在高斯整数 $\alpha 和 \beta$ 使得 $\alpha \beta = z$ ,则称 $\alpha$ 整除 $z$ ,记作 $\alpha | z$ .

5、高斯整数的取模运算：

我们知道，实整数之间是可以进行取模运算的，那么高斯整数能否进行取模运算呢？答案是肯定的：

运算规则如下：

$z\mod p = z- \left \lfloor \frac{z}{p} \right \rfloor \times p$

三、高斯素数：

1、定义：

对于非 $0$ 高斯整数 $\pi,若\pi \ne \varepsilon$ ,且 $\pi$ 只能被 $\varepsilon$ 及其相伴整除，那么称 $\pi$ 为高斯素数。

2、性质：

若 $\pi 为高斯素数，则：$

1、 $\bar\pi为高斯素数$ ：

证明： $假设\bar\pi不是高斯素数$

$那么存在不为单位的高斯整数\alpha ,\beta ,使得\bar \pi = \alpha \beta$

$那么，\pi = \bar \alpha \bar \beta,其中\bar \alpha 、\bar \beta 均不是单位$

$这与\pi是高斯素数矛盾$

$故假设不成立，\bar \pi 是高斯素数$

2、 $\varepsilon\pi也是高斯素数(证明与1类似，略)$

3、整数唯一分解定理的拓展：

和整数的唯一分解定理一样，高斯整数也有唯一分解定理，即高斯整数也可以分解成若干高斯素数相乘，且分解结果唯一（在不考虑相伴的情况下）。

分解的方法我们在后面给出（先挖个坑）。

4、高斯素数和整数素数的联系（费马二平方定理）：

首先，整数中的合数一定不是高斯素数
整素数不一定是高斯素数： $\times (1+i),5=(2-i)\times(2+i)$

那么，什么整数素数是高斯素数呢？接下来，我们介绍一下费马二平方和定理。

费马二平方定理：

引子：

在介绍这个定理之前，让我们想一下，若一个素数p 能被分解成两个非0，且非单位的高斯整数 $z_1,z_2$ 相乘，那么 $z_1,z_2$ 应该满足什么条件呢？

答： $z_1,z_2$ 要共轭.

让我们来证明一下：

设 $z_1 = a_1 + b_1i,z_2= a_2 + b_2i，且 |a_1|>=|a_2|$ .

那么为了使 $z_1,z_2$ 的乘积中的虚部为0，必然有 $\frac{a_1}{a_2}=-\frac{b_1}{b_2}$

所以 $a_1a_2$ 与 $b_1b_2$ 异号。

所以为了让乘积的实部 $a_1a_2+i^2b_1b_2>0$ , $a_1,a_2$ 要同号

我们设 $\frac{a_1}{a_2}=t$ >=1,t为实整数.

则 $z_1 = t(a_2-b_2i)=t\bar z_2$

那么 $p = t (a_2^2-i^2b_2^2)$ ,其中 $a_2^2-i^2b_2^2)<=p$

接下来，我们证明 t = 1（即证明 $a_2^2-i^2b_2^2=p)$ ;

若 $a_2^2-i^2b_2^2)<p$

则 $\frac{p}{a_2^2-i^2b_2^2}$ ,由于 $p$ 是质数,且 $a_2^2-i^2b_2^2)<p$ ，所以分子分母互质

而 $a_1 = a_2 \times t=a_2 \times \frac{p}{a_2^2-i^2b_2^2}$

所以，要使 $a_1$ 是整数，只有当 $a_2$ 是 $a_2^2-i^2b_2^2)$ 的倍数时才成立，显然，对于非单位高斯整数来说，这是不可能的

所以 $a_2^2-i^2b_2^2=p$ .

所以 $t = 1$ ;

所以 $z_1,z_2$ 共轭.

(注意到，我们的推导 $z 1, z 2$ 共轭这个结论时并没有使用到 $i^2=-1$ 这个条件，所这个结论可以推广到 $\sqrt{-k}$ 的情况。）

内容：

奇素数 $p$ 能表示成 $a_2^2+b_2^2 \Leftrightarrow p \equiv 1(mod 4)$

根据这个定理和我们的引子，我们可以知道： $(4 K + 1)$ 型素数不是高斯素数，而 $(4 k + 3)$ 型素数一定是高斯素数.

5、分解 $(4 k + 1)$ 型素数 $p$ 的方法：

1、枚举 $1$ 到 $\sqrt{p}$ 的所有整数，找出一个符合条件的即可。

6、高斯素数判定的充分必要条件：

设 $z = a + bi$ ,当且仅当 $z$ 满足下述条件之一时， $z$ 是一个高斯素数：

1、 $a = 0$ ， $b$ 是 $4 k + 3$ 型素数

2、 $b = 0$ , $a$ 是 $4 k + 3$ 型素数

3、 $a$ , $b$ 均不为 $0$ ， $N (z)$ 是素数

1、2比较显然，我们对3做出证明：

…

先证明充分性：即证明： $N (z) = p$ , $p$ 是素数 $\Rightarrow z$ 是高斯素数

假设z不是高斯素数，则存在非零且非单位高斯整数 $\alpha ,\beta$ 使得 $\alpha \beta=z$ ；

那么根据范数的性质得： $N(z)=N(\alpha)N(\beta)=p$ ，其中 $N(\alpha)$ , $N(\beta)$ 是大于1得整数.这与 $p$ 是素数矛盾

故假设不成立,所以 $z$ 是高斯素数.

（证到这里，我们结合之前介绍费马平方和定理时给出的引子，就可以得出一个结论，由整素数分解成的两个高斯整数（如果该整素数本身不是高斯素数的话），必然共轭且为高斯素数。）

**再证明必要性：**即证明： $z$ 是高斯素数 $\Rightarrow N(z)$ 素数。

设 $N(z)=z\bar z=p_1\times p_2\times p_3 \times...\times p_n$ ， $p_i$ 为整素数( $i = 1, 2, 3... n$ )。

由于 $z$ 是高斯素数，且 $z ∣ N (z)$ ,所以 $z$ 是 $N (z)$ 在复数范围内分解质因子的一部分。

所以 $z$ 是由 $N (z)$ 在完成整数质因子分解后，进一步将一些不是高斯素数的整素数分解成高斯素数后得到的。

所以存在且仅存在一个 $p_i$ ，使得 $z|p_i$ 。

根据介绍费马平方和定理时给出的引子，我们知道素数 $p_i$ 若能表示成两个高斯整数的乘积，则这两个高斯整数共轭且为高斯素数。

所以， $z\bar z=p_i$ , 即 $N(z)=p_i$ ,必要性得证。

（对3的证明并没有用到 $i^2 = -1$ 这个条件，所以3可以推广到 $\sqrt{-k}$ 的情况）

7、在复数范围内将实整数分解成高斯质因数得方法

根据上面六部分内容,我们可以总结出：

$(4 k + 3)$ 型的素数是高斯素数。
$(4 k + 1)$ 型的可以分解为两个共轭的高斯素数。

所以，要将一个整数分解成若干个高斯素数相乘，只要先将其分解成实实质因数，再将 $(4 k + 1)$ 型的素数分解成对应得高斯素数即可即可。

（注意，这个方法并不能推广到 $i=\sqrt{-k}$ 得情况，因为费马二平方定理是素数 $a^2+b^2 \Leftrightarrow p \equiv 1(mod 4)$ ，而不是 $p=a^2-i^2b^2\Leftrightarrow p \equiv 1(mod 4)$ ）

8、将高斯素数的判定推广到 $\sqrt{-k}$ , $(k > 1)$

那么对于形如 $b\sqrt{-k}$ 的高斯整数，如何判定它是不是高斯素数呢？

$a = 0$ 时，当且仅当 $b = 1$ 时， $z$ 是高斯素数。
$\ne 0$ , $b = 0$ 时，判断 $a$ 能否被表达成 $t (x^2 + k y^2)$ 的形式（可以通过上面证明的引子来证明）。
a,b均不为 $0$ 时，只要判断 $N (z)$ 是不是素数即可。

四、例题

1、uva 1415 - Gauss Prime

题意：
给出一个高斯整数： $\sqrt{-2}$ ,保证 $\ge 0$ , $b > 0)$ 。

判断 $z$ 是不是高斯素数，是则输出“Yes",否则输出”No"。

解析：

$a = 0$ 时，仅当 $b = 1$ 时输出”Yes" (然而这样会 wa，改成 $a = 0$ 则输出“No”就过了，感觉这题怪怪的，圈红的地方又说 $\sqrt{-k}$ 是高斯素数）。

$\ne 0$ 时，判断 $a^2+2b^2$ 是不是素数即可。

#include<iostream>

using namespace std;

int n,a,b,temp;

bool check(int x)
{
    for(int i=2;i<=x/i;i++)
    {
        if(x%i==0)return false;
    }
    return true;
}

int main()
{
    cin>>n;
    while(n--)
    {
      	cin>>a>>b;
        if(a==0)
        {
            if(b==1)cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
            //改成 cout<<"No"<<endl,才能ac
        }
        else 
        {
            temp = a*a + 2*b*b;
            if(check(temp))cout<<"Yes"<<endl;
            else cout<<"No"<<endl;
        }
    }
	return 0;
}

2、洛谷 2508 圆上的整点数：

贴上一个很好的视频链接（这个视频真的讲的非常好）：官方双语

思路： $x^2+y^2=r^2\Longleftrightarrow (x+yi)(x-yi)=r^2$ 。

相当于让我们计算有多少对共轭高斯整数的乘积是 $r^2$ 。

复习一下共轭的一个性质： $\overline{zw}=\bar z \bar w$ 。

那么，怎么才能计算所有符合条件的共轭对的数量呢？

实际上，我们可以把 $r^2$ 在复数范围内分解成一系列高斯素数的乘积，在不考虑相伴的情况下，这种分解是唯一的。

我们假设 $2^n \prod_{i=1}^{i=m}p_i^{k_i} \prod_{j=1}^{j=n}q_j^{r_j}$ ，

其中 $p_i$ 为 $(4 k + 1)$ 型素数， $q_j$ 为 $(4 k + 3)$ 型素数，那么每个 $p_i$ 都可以分解为一对共轭复数，

所以 $(1-i)^n(1+i)^{n}\prod_{i=1}^{i=m}z_i^{k_i}\bar z_i^{ki}\prod_{j=1}^{j=n}q_j^{r_j}$ ，

所以 $r^2 = (1-i)^{2n}(1+i)^{2n}\prod_{i=1}^{i=m}z_i^{2k_i}\bar z_i^{2ki}\prod_{j=1}^{j=n}q_j^{2r_j}$ ，

我们要计算满足 $r^2 = z\bar z$ 的共轭对有多少种，也就是计算 $r^2$ 的素因子有多少种不同的分配方式可以将素因子分配到两边,使得两边的乘积是一个共轭对。

我们先来看一个例子：

r = 5

那么 $r^2=25=(5*5)=(1+2i)^2(1-2i)^2$ ，

我们得到了一种由（4k+1)型素数5分解得到得共轭对（1，2），（1，-2），共有两组：

第一种分配方案：（1，-2）全在右边。

（1，2）（1，-2）共轭，

（-3，4）（-3，-4）共轭，

第二种分配方案：一个（1，-2）在右边，相当于第一种方案交换第一行两边的数，

（1，-2）（1，2）共轭，

（1，2）（1，-2）共轭，

（5，0）（5，0）共轭，

第三种分配方案：0个（1，-2）在右边，相当于第二种方案再交换第二行两边的数，

（1，-2）（1，2）共轭，

（-3，-4）（-3，4）共轭，

这三种方案分别对应圆上（-3，4），（-3，-4），（5，0）这三个点。

但是，这就是所有的点了吗？

并不是，如果我们给每个结果的左边乘上 $i$ ,右边乘上 $- i$ ,我们将再次得到三个点：

（-4，-3），（4，-3），（0，5）

如果左边乘上 $- i$ ,右边乘上 $i$ ,我们也将再次得到三个点：

（4，3），（-4，3），（0，-5）

如果左边乘上 $- 1, 右边乘上$ $- 1$ ,我们也将再次得到三个点：

（3，-4），（3，4），（-5，0）

让我们回忆一下，复数乘法在复平面的几何意义：模长相乘，相位角相加，而

（1，0），（0，1），（0，-1），（-1，0）的模长都是1，相位角分别是0， $\pi/2,\pi,3\pi/2$ .

那么我们上面三种操作就相当于将一开始的三个点分别旋转90°，180°，270°。只要我们一开始取到的点不存在夹角为90°，180°，270°的两个点，那么就不会重复。

我们再来看一个例子：

$r^2$ = 5 * 5 * 3 * 3 = (1-2i) (1+2i) 3 .

这里多了一个无法继续分解的 $(4 k + 3)$ 型素数 3，由于整数的共轭还是它本身，所以我们分配3的时候，无论怎么交换3及其共轭，都不会产生新的结果，我们只要保证左右两边3的个数相同即可，所以3并没有对我们的结果做出贡献，所以半径为 $5 * 3$ 的圆上也只有 $3\times4=12$ 个点。

我们再看一个例子：

$r^2=2*2=(1-i)^2(1+i)^2$

接下来我们来分配共轭对 $(1 ， - 1) ， (1 ， 1)$ ；

第一种方案：

（1，-1）（1，1）共轭

（0，2）（0，-2）共轭

第二种方案：

（1，1）（1，-1）共轭

（1，-1）（1，1）共轭

（2，0）（2，0）共轭

第三种方案：
（1，1）（1，-1）共轭

（1，1）（1，-1）共轭

（0，-2）（0，2）共轭

这样，我们的得到了三个点：（0，2）、（0，-2）、（2，0），这三个点有点特殊,他们之间的夹角分别是90°，180°，270°。也就是说，这三个点中得两个点可以由另外一个点乘上单位（i，-i，-1，1）得到，也就是说，我们交换左右两边的（1，-1），（1，1）产生的效果与我们最后对结果乘上单位的效果是一样的，所以我们把2的分配方案视为1，因为无论如何我们最后都可以对结果乘上单位，已经包含了2能产生的所有效果。但是，有没有其他的高斯素数交换共轭对对结果产生的影响与乘上单位产生的影响一样呢？显然是没有的（留给读者自证）。

最后，我们再来看一个例子：

$r^2= 3^2\times 5^2 \times 2^2\times 17^2$

对3进行分配，每种方案都相同，故对3只有一种分配方案（注意，如果3只有奇数个，方案为0，但是 $r^2$ 作为一个平方数，每个整数质因子必然有偶数个）.

对 5 分解出来的共轭对（1，2），（1，-2）分配，由于有两组（1，2）、（1，-2），我们一共有3种分配方案（左边分配0、1、2个（1，2））。

对17也是一样的，有3种分配方案（因为5和17的次数相同）

对于2，他对结果并无贡献，方案记为1。

所以方案总数为：3 $\times 3 = 9$ 种，每种方案都对应一个点，最后每个点乘上单位（i,-i,1,-1) 又会得到3个新的点，所以我们的总共又 9x4 = 36个点。

所以对于 $r^2 = (1-i)^{2n}(1+i)^{2n}\prod_{i=1}^{i=m}z_i^{2k_i}\bar z_i^{2ki}\prod_{j=1}^{j=n}q_j^{2r_j}$ ,

即 $(1-i)^n(1+i)^{n}\prod_{i=1}^{i=m}z_i^{k_i}\bar z_i^{ki}\prod_{j=1}^{j=n}q_j^{r_j}$ 的情况：

我们的点一共有 $\prod_{i=1}^{2*k_i+1}$ ,

代码：

#include<iostream>
#include<cstring>
#include<algorithm>
#define int long long 

using namespace std;
int r;
int ans=1;
signed main()
{
    cin>>r;
    for(int i=2;i<=r/i;i++)
    {
        if(r%i==0)
        {
            int s=0;
            while(r%i==0)
            {
                s++;
                r/=i;
            }
            if(i==2||i%4==3)s=0;
            ans *= (2*s+1);
        }
    }
    if(r>1&&r%4==1)ans *=3;
    cout<<4*ans;
}

zmlbsdd

关注

3
点赞
踩
5

收藏

觉得还不错? 一键收藏
4
评论
高斯素数判定

对于复数zabiz = a + bizabi,定义zzz的共轭为zˉa−bizˉa−bi23i12i2+3i,1+2i23i12i等等，对应着复平面上的整点。（若将i−1i−1,替换为i−ki−k，这样的数也叫高斯整数，但不一定满足整数唯一分解定理，现如今数学家们已经证明当且仅当k1237111967163k1237111967163时整数唯一分解定理成立）
复制链接

扫一扫