最小生成树问题——Prim算法

最新推荐文章于 2023-09-17 13:11:35 发布

原创

最新推荐文章于 2023-09-17 13:11:35 发布 · 684 阅读

CC 4.0 BY-SA版权

Prim算法是一种解决无向连通带权图最小生成树问题的贪心算法，从一个顶点出发，每次选择当前可用的最小权值边将顶点加入生成树，直至所有顶点都被包括。其时间复杂度为O(n²)，适用于稠密图，可以通过堆优化提升到O(mlogn)。

最小生成树问题
设G=(V,E)是无向连通带权图，即一个网络。图中每一条边(u,v)的权是c[u][v]，表示联通u与v的代价。如果G的子图T是一棵包含G的所有顶点的树，则称T为G的生成树。生成树上各边权的总和称为该生成树的耗费。在G的所有生成树中，耗费最小的生成树称为G的最小生成树：

算法思想：贪心算法
贪：每一步都要最优
好：权重最小的边
Prim算法基本思想：让一棵小树长大
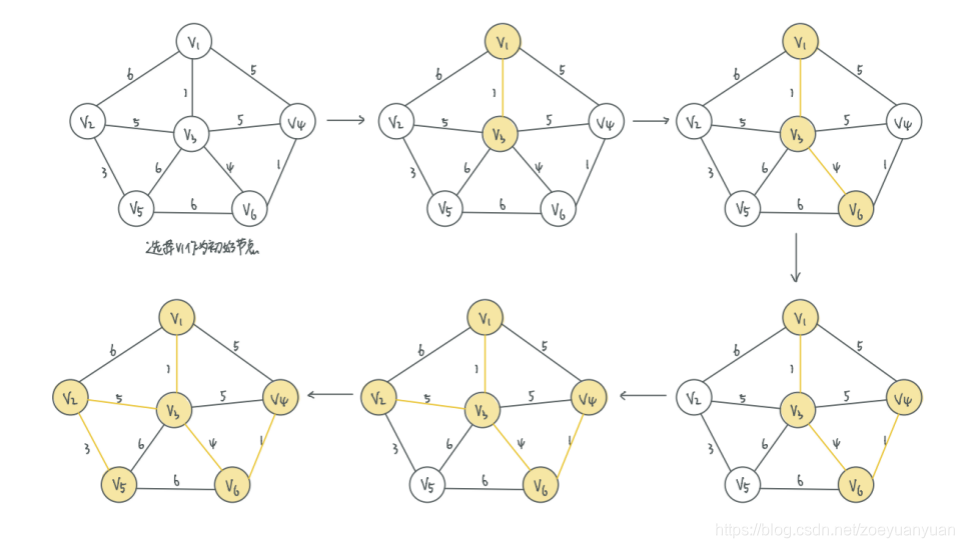
- 以顶点为主导地位，从起始顶点出发，通过选择当前可用的最小权值边把顶点加入到生成树当中来：
- 从连通网络N={V,E}中的某一顶点U0出发，选择与它关联的具有最小权值的边（U0,V）,将其顶点加入到生成树的顶点集合U中。
- 以后每一步从一个顶点在U中，而另一个顶点不在U中的各条边中选择权值最小的边(U,V),把它的顶点加入到集合U中。如此继续下去，直到网络中的所有顶点都加入到生成树顶点集合U中为止。