CodeChef Chef and Strange Operations

Chef and Strange Operations

Chef has an array A consisting of N integers (1-based indexing). He asks you to perform the following operation M times:

for i = 2 to N:
    Ai = Ai + Ai-1

Your task is to find the xth element of the array (i.e., Ax) after performing the above operation M times. As the answer could be large, please output it modulo 10^9 + 7.

Input

• he first line of input contains an integer T denoting the number of test cases.
• The first line of each test case contains three space-separated integers — N, x, and M — denoting the size of the array, index of the element you need to find, and the amount of times you need to repeat operation before finding the element, respectively. The second line contains N space-separated integers A1, A2, …, AN.

Output

For each test case, output a single line containing one integer: Ax modulo 109 + 7.

Constraints

• 1 ≤ T ≤ 10
• 1 ≤ x ≤ N ≤ 10^5
• 1 ≤ M ≤ 10^18
• 1 ≤ Ai ≤ 10^18

Subtasks

Subtask 1 (8 points):

• 1 ≤ x ≤ min{2, N}

Subtask 2 (24 points):

• 1 ≤ N * M ≤ 106

Subtask 3 (68 points): No additional constraints

Example

Input:

2

3 2 3

1 2 3

3 3 3

1 2 3

Output:

5

15

Explanation

Values in the array A:

Before the operations: [1, 2, 3]
After the first operation: [1, 3, 6]
After the second operation: [1, 4, 10]
After the third operation: [1, 5, 15]

Task：

给定一长度为$n$的序列，每次运行如上所示的代码，共进行$M$次。求最后x位置的元素大小，即$A[x]$,对P取模$(n<=10^5,M<=10^18,A[i]<=10^18,P=10^9+7)$

Solution：

比赛的时候根本不会写…写个了暴力收场。

首先我们肯定要求出答案中每个数在答案中出现的次数，然后加起来。这是显然的。通过一些奇特的打表法，我们可以得到一个杨辉三角。

//打表程序
#include<stdio.h>
int A[20];
int main(){
    A[1]=1;
    for(int i=1;i<=10;i++){
        for(int j=2;j<=10;j++)
            A[j]=A[j-1]+A[j];
        for(int j=1;j<=10;j++)
            printf("%6d ",A[j]);
        puts("");
    }
    return 0;
}
/*
    1      1      1      1      1      1      1      1      1      1
    1      2      3      4      5      6      7      8      9     10
    1      3      6     10     15     21     28     36     45     55
    1      4     10     20     35     56     84    120    165    220
    1      5     15     35     70    126    210    330    495    715
    1      6     21     56    126    252    462    792   1287   2002
    1      7     28     84    210    462    924   1716   3003   5005
    1      8     36    120    330    792   1716   3432   6435  11440
    1      9     45    165    495   1287   3003   6435  12870  24310
    1     10     55    220    715   2002   5005  11440  24310  48620
*/

由于这个答案的特殊形式，我们可以发现当前$x$位置的数与上一行的表格中的数有关。（其实是打表发现的）

规律：

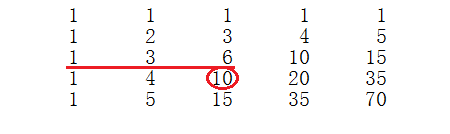
对于第四列的$A_3=6A_1+3A_2+A_3$，观察可以发现这就是上一行的前三个数字，可以用组合算出来：$1=C_2^0,3=C_3^1,4=C_4^2$。我们只需要算出这几个数字即可。

由于$m$的规模可以达到$10^{18}$，因此我们用递推式计算：$C_{n+1}^{m+1}=\frac{(n+1)!}{(m+1)!(n-m)!}=\frac{n!}{m!(n-m)!}*\frac{n}{m}=C_n^m*\frac{n}{m}$

附：O(n)逆元：

设 $a=P/i,b=P%i$

$a*i+b\equiv0(mod P)$

$a*i\equiv-b(mod P)$

$-a*b^{-1}\equiv i^{-1}(mod P)$

因为 $b<i$，因此直接递归求解即可，复杂度$O(n)$

#include<stdio.h>
#include<ctype.h>
#define ll long long
#define M 100005
#define P 1000000007
int A[M],F[M];
inline void Rd(int &res){
    char c;
    ll rs=0;
    while(c=getchar(),!isdigit(c));
    do{
        rs=(rs<<3)+(rs<<1)+(c^48);
    }while(c=getchar(),isdigit(c));
    rs%=P;
    res=rs;
}
int f(int x){
    if(F[x]!=0)return F[x];
    if(x==1)return F[x]=1;
    int a=P/x,b=P%x;
    return F[x]=(1LL*(-a)*f(b)%P+P)%P;
}
int main(){
    int n,x,m;
    Rd(n);Rd(x);Rd(m);
    for(int i=1;i<=n;i++)
        Rd(A[i]);
    for(int i=1;i<=n;i++)
        F[i]=f(i);
    int sum=1,t=0,ans=0;
    for(int i=m;i<=m+x-1;i++){
        ans=(ans+1LL*sum*A[x-t]%P)%P;
        t++;
        sum=1LL*sum*i%P*F[t]%P;
    }
    printf("%d\n",ans);
    return 0;
}