机器学习的数学-分类

文中来自立石贤吾《白话机器学习的数学》的学习总结。

一、一个二分类问题

下面的两个图，一个是纵向，一个是横向，如果知道他们的长、宽，就很容易通过一个简单的逻辑表达式完成分类：如果将这样的两种图片进行分类 ，即长<高是否成立。

 但是我们可以通过机器学习来解决。从上图可以得到下面的数据，我们就可以用作训练数据。其中的宽、高两列是数据，形状一列是标签，这也是分类常用的数据展示格式。

 将上述的数据放在坐标图上：

上图的白点是纵向图片，黑点则表示横向图片。在本例中，在坐标图上也很容易看出图片的纵横关系，但是实际中的数据经常表示一些抽象的量，因此不会这么明显。比如，这里的的x和y这个二维的坐标系中表示的量是灰度值这样的量，也没有问题。

机器学习的学习过程中经常遇到的一个问题是实现手写数字的识别，在这里可以做一个类比：

手写数字识别是通过判断一副图片中的像素点的灰度值的分布来确定的，它的维度也就是图片的像素点的个数。而这个例子中只需判断图片的纵向和横向，用长和高两个量来决定就足够了。

但只通过上面的两个数据还不太能说明问题，再加入一些数据： 

 

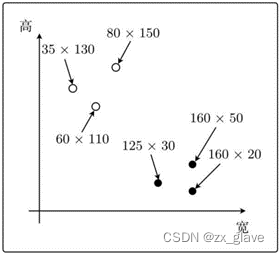
显然，我们可以通过一条线来对上图中的点进行分类，如下图所示，分类的目的就是找到这条线。 

 二、内积

 直接插入内积的内容其实有点让人摸不到头脑，但是学完以后，再接下来的内容就会方便一些。

《白话机器学习的数学》中有一句拗口的话：使权重向量成为法线向量的直线。这句话很不好理解，接下来的内容基本就是围绕这句话展开讲解的。

 这个式子表示两个向量的内积是0，在向量空间的坐标系中，就表示一条直线。也可以这样写：

 其中的w就表示权重向量。如果我们想把上节中实现分类的直线也用这种形式表示当然也可以，它是一个二维坐标系，因此像下面的形式就可以：

 就像回归中的未知参数θ一样，w也是参数。这样看其实二者十分相似。

 比如，我们设权重向量为w=(1,1)，则得到法线向量为：

在坐标系中表示，同时画出它的法线：

 

 内积的另一种表示方式，就是在极坐标系中：

 表达式中的|w|和|x|是向量的长，因此必定是正数。所以要想使内积为0，只能使cos θ=0。要想使cos θ=0，也就意味着θ=90◦或θ=270◦。这两种情况也是直角。

 我们的最终目的是找到上图中的虚线，求出它的权重向量，这条直线也就自然就知道了，就像回归中求各个项下系数。

介绍到这里，再看使权重向量成为法线向量的直线这句话，我依然觉得别扭，但是依稀、可能、似乎、大概能理解了。

三、感知机

上面一节插入内积内容的目的就是为了介绍感知机的相关概念。

感知机是接受多个输入后将每个值与各自的权重相乘，最后输出总和的模型。

这个图在这里并不会对我们的理解有太多的帮助，但是后续学习神经网络，就会比较形象。

这里啰嗦几句，其实分类和回归一个很大的不同就是：回归可以很自然的和我们之前学习的常见函数结合起来，像二维坐标中的直线，抛物线，哪怕更加复杂的曲线。它都是可以用一个表达式表示出来的连续曲线。但是现在来看分类，即使是这样一个简单的二分类，我们也找不到一个“标准”的函数来描述它，因为它是跳跃的，不连续的。

不过话说回来，即使是这样的情况我们依然可以很直接的想到，可以用分段函数来表示，在这一点上，我们就和回归统一起来了。那么它的形式是什么样的呢？

对于二分类来讲，我们可以选择两个不同的值表示两种分类，比如常见的可以选择0和1，1和-1，甚至你可以选择1和100，在感知机里最好用1和-1表示，你会发现这样会减少很多计算量。

那么我们就可以写出分类的函数表达式：

 先等等，后面的条件很眼熟，原来就是上面介绍的内积。我们用了一个内积表达式来作为判别条件，而不是采用通常用的横坐标，虽然表达式中包含了横坐标。

这里比较让人迷糊，但可以和回归对比着来：fw(x)这个函数才相当于回归中的回归表达式，而后面的内积表达式只是作为一个判断条件，在回归中找不到对应的地方，这里取了一个新的名称，叫做判别函数。

这个判别函数，也就是内积，我们上面做了研究了，写成下面的形式更好理解：

也就是样本表示的向量同权重向量w之间的夹角为θ. 这个θ这里很关键。因为绝对值都是非负的，那么它的正负就完全依赖于后面的cosθ。而cos的函数形状如下：

 

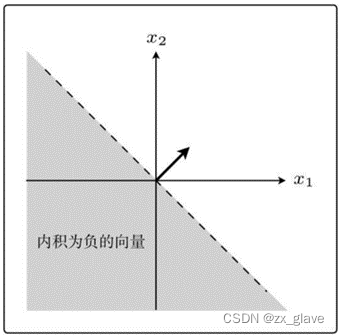
可以看出，在90◦＜θ＜270◦范围内的所有向量都为负，其他都是非负。如下图所示：

   

 

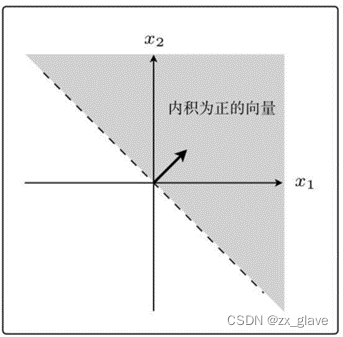
 直接提出感知机的更新表达式虽然有点突兀，但是有了上面的知识，就可以理解了，它的更新表达式是这样的：

更新表达式在回归的时候已经接触过了，目的就是求回归表达式的系数，而这里求的是判别函数的系数，这是有点不同的。 

更新表达式由两部分组成，分别来看。

第一部分表示，通过判别函数对宽和高的向量x进行分类的结果与实际的标签y不同，也就是分类错误。

第二部分表示，通过判别函数对宽和高的向量x进行分类的结果与实际的标签y相同，也就是分类是正确的。直接把w赋给了新的w，没有做任何改变。

着重看一下分类错误的时候，更新表达式是如何起作用的。

先给出训练数据，这些数据并不陌生，但是最后一列y表示：当为纵向时，标注为-1，横向时标为1.用x1和x2分别表示长宽。

跟回归时一样，先随意画一个向量w，然后用x(1)=(125,30)来更新参数。

 现在权重向量w和训练数据的向量x(1)二者的方向几乎相反，w和x(1)之间的夹角θ的范围是90◦＜θ＜270◦，内积为负。也就是说，判别函数fw(x(1))的分类结果为-1。但其实它是横向的，也就是1，这说明分类失败。在这种情况下就要通过更新表达式的第一部分进行更新，将y=1带入，得到：

 从图上看更清楚，这里是一个向量的加法，也可以看出来，之所以用1和-1来表示纵向和横向，也是为了这里的运算更加简单。

 需要注意的是，我们一直使用的是w向量，而不是实际用于分类的直线来进行运算的。这也体现了之所以要引入向量的原因。上图中虚线表示实际分类直线的变化情况，也是很直观的。

从下图也可以看出来θ＜90，说明现在的分类是正确的。

 这样，利用训练数据逐渐迭代，最终就应该能得到比较符合实际的分类函数。

 

四 、线性可分

线性可分指的就是能够使用直线分类的情况，像上面的例子，用一条直线就可以完成分类，但是如下图中的情况，就不能简单的用一条直线进行分类，这就属于线性不可分的。

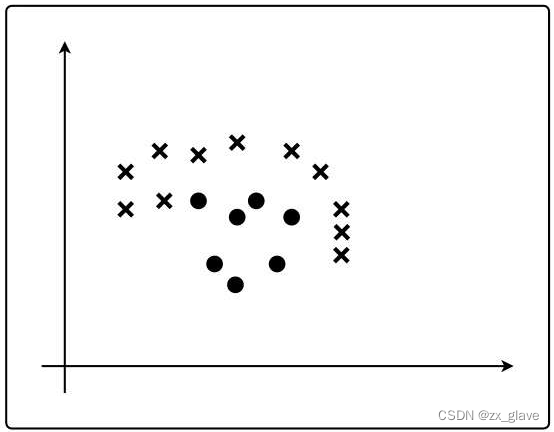
总之，上面对单层感知机的介绍，基本在实际中用不到，因为实际问题往往要复杂的多，那么就需要用到多层感知机，而多层感知机就是神经网络了。

 

五、逻辑回归 

从名字上来看，这个概念就很有意思。明明是分类的方法，却叫做回归。我们知道，回归与分类的区别：回归对应的是连续的问题，而分类一般是不连续的。用连续的方法去解决不连续的问题，我们其实比较容易想到通过概率来实现这一点。

在感知机中，我们就很硬性的将二分类问题分为是与不是，并将这一点很明确的体现在了函数当中。那我们是不是有什么方法比较和软的对待这个问题呢？

就像分类图片横向与纵向的问题，虽然有长宽相等的情况将图片的纵、横一分为二，但是显然有些图像虽然是纵向的，但它可能更接近于横向；有些横向的图像，也更接近于纵向。就像彩虹一样，各种颜色的过度并没有一个明显的界限的。

有了这样的想法，我们就可以用一个连续的函数来表示图片的纵横了，虽然我们不能说这个图片有35%是横向，65%是纵向，但是我们可以假想，就是有这样一个谱系，每一个图片都能在这个谱系中找到自己的位置，以表明它的形状。我们不一定要定量的描述，只需描述清楚他们的趋势就可以。比如说，有两个图片，只要能表示出相比之下哪个图片更接近于横向，或纵向就可以了，而不需要精确的表示出究竟差了多少。

于是我们就找到了这样一个叫做sigmoid的函数，可以很完美的解决这样一个问题。

它在坐标上的表示是这样的：

 看出什么没有呢？它的大小是(0,1),在横坐标为0的时候，它的值是0.5，不偏不倚，正好是0到1的中间。这样的特点放到我们的问题中堪称完美。

0＜fθ(x)＜1这个特征就说明，它可以用作概率来使用。

而θTx=0时fθ(x)=0.5的特征，就可以用来作为分类的界限。

 因为我们的目的就是一个暴力划分的问题，因此这样一个看起来很暴力的函数仍然避免不了，但是要注意的是，判别函数中包含了更准确的信息。

在感知机中，我们直接的用了w·x与0的比较，而这里我们在外面又包了一层，这里虽然写成了的形式，但揪其本质，仍然是一样的意思。

 总之，判别函数有了一个含义，就是概率，具体到我们的问题就是图片是横向的概率。当概率大于0.5的时候，就分类为横向，小于0.5的时候就分类为纵向的。

我们再改一下训练数据的形式：

那对于一个训练数据，我们期待的是：

如果这个训练数据被认定为横向，也就是1，我们就希望判别函数最大。

如果这个训练数据被认定为纵向，也就是0，我们就希望判别函数最小。

换成数学语言：

● y=1的时候，我们希望概率P(y=1|x)是最大的

● y=0的时候，我们希望概率P(y=0|x)是最大的

把所有训练数据的概率相乘，就是最终的概率，我们当然希望这个概率最大。

可以写成这样： 

 

 这叫似然函数。

加log，并不影响结果，并且可以解决概率越乘越小的问题。这就是我们的目标函数。

求导就可以了。回头补上。

后面的推导一堆数学公式，最终结果是这样的，也就是更新函数

 

 六、线性不可分

线性不可分问题之前提过，是不能用单层感知机解决的，但是可以通过逻辑回归解决。

通过加平方项，可以实现弯曲。

 

 也就是这样：

假设：

 带入：

 在图上表示：

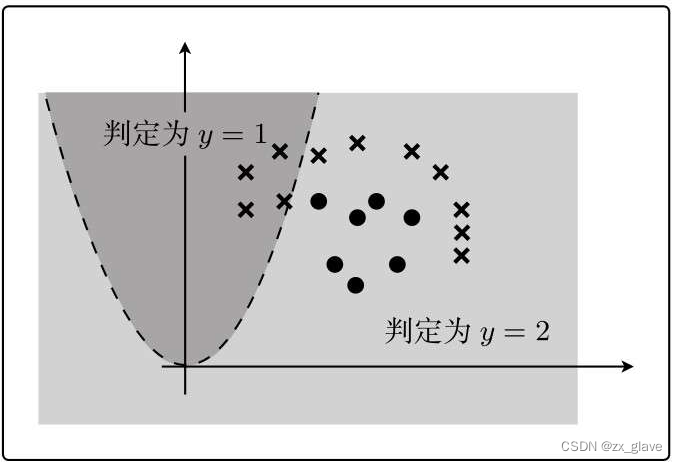
那么经过随机梯度下降法，就可以逐渐求出比较合理的结果了。