上期我们将二次成本函数改进成了交叉熵成本函数C,显著的提高了训练的效率。可以确定的是,每个周期的训练,成本函数都在减小,以此优化神经网络中的参数。然而有没有人想过,C的减少真的在优化参数么?,特别是结合第三期的这张图看:
可以确定的是,周期27的C一定是比周期26小的,然而识别率并没有相应的提高,那么下一个周期我们训练出来的参数还靠谱么。
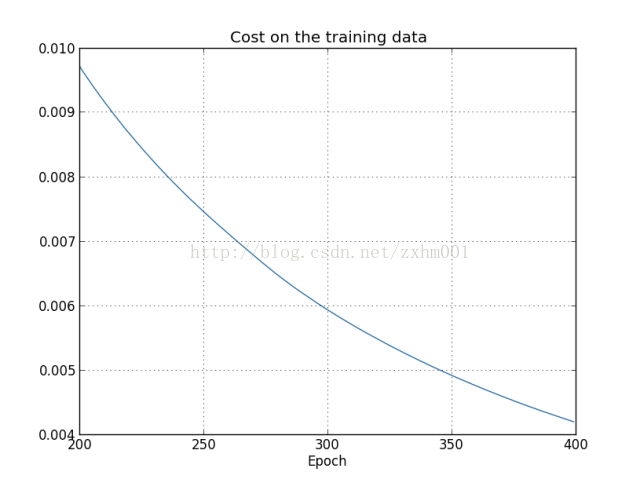
作者为了更好的说明这个问题,做了一个实验。他选取50000个训练数据集中的前1000个作训练数据,训练400个周期,在训练过程中,函数C的变化曲线图如图:
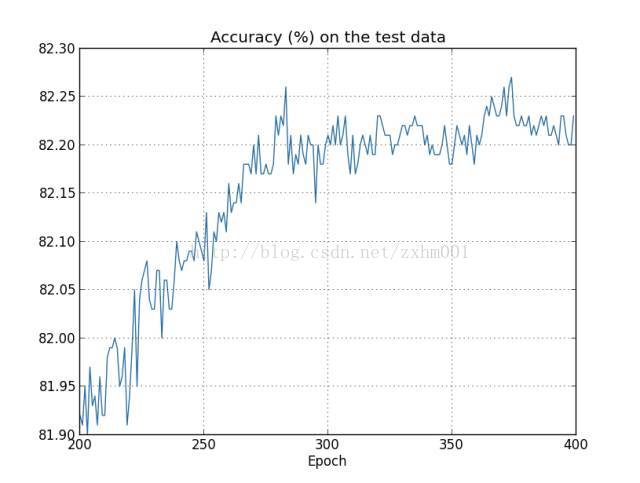
很明显,当训练到第280周期左右,识别率的上升就基本停止了,稳定在82%左右。这种C还在不断变小,但是识别率没有提升的情况,就说明我们的神经网络在280训练周期之后就过度拟合(Overfitting)了。
其实我们拿第280周期训练出来的神经网络和第400周期训练出来的神经网络去识别训练数据集,400周期的识别率会高很多。也就是说,过度拟合的过程,是神经网络在学习完了训练数据集的通用特征之后,去学习他的特有特征或者噪音了,以至于虽然对训练数据集而言识别率更高了,但是对其他数据并没有什么卵用。我们再来看几张图:
第一张是原始数据,或者在神经网络里面是训练数据:
目的是想建立y=f(x)的一个模型。
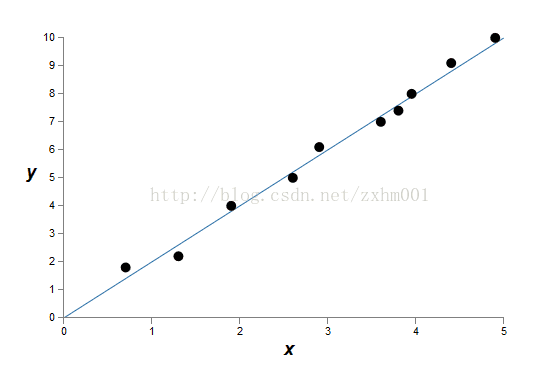
第二张是正常拟合的情况:
第三张是过度拟合的情况:
显然,第三张图对已有的数据来说,已经做到了精确完美拟合,但是他对其他数据并没有用。第二张看似没有完美拟合,但是更有通用性。
为了避免这种情况,让训练更有效率,我们就需要监测什么时候就开始过度拟合。其实从原理来说,监测过度拟合还是挺简单的,只要一直记录测试数据的识别率,当识别率开始不再上升的时候,就说明开始过度拟合了。但实际上,我们不会使用测试数据,而是会使用另外一个数据集:验证数据。在第三期的代码里面,有这么一行,training_data, validation_data, test_data = mnist_loader.load_data_wrapper(),我们之前用到了训练数据集training_data,测试数据集test_data,并说明这两个数据集是出自不同采样人群的手书。现在要用到验证数据集validation_data。这个数据集与测试数据集的结构完全一样,但是出自不同采样人群。每个训练周期记录验证数据集的识别率,当他不再上升的时候,就停止训练,避免过度拟合。
但是为什么要使用验证数据集而不是测试数据集呢,实际上这是为了让我们的神经网络更具通用性。假设用测试数据集来确定训练周期,再用测试数据集来测试神经网络的识别率,那么怎么有信心以后遇到任何一个数据集,这个神经网络的测试率都有这么高呢?换一种说法,我们怎么能确定,这个训练周期不是专门为测试数据量身定制的呢?所以要引入一个验证数据集,来确定训练时候需要的参数。因为验证数据集和测试数据集来自不同的样本人群,如果这些参数对测试数据集都合适,那对我们就有信心对其他数据也合适了。
那其实第一个解决过度拟合的方法就很明显了,因为过度拟合是学习完通用的特征之后,就去学习噪音了,那我让训练数据集足够多,这种噪音就被放小了。
另外一种方法,是我们今天要重点讲的,叫正则化(regularization)。正则化的技术有很多,这期详细讲一种叫L2正则化法,也叫权重衰减(weight decay)正则化法。既然有L2,就会有L0和L1啥的,下期再来介绍其他的正则化技术。
为啥叫权重衰减正则化技术呢。我们先看我上面表面过度拟合的那张曲线图。过度拟合精确的拟合了所有的训练数据,也就是学习了噪音,就会导致函数的波动会相当大,也就是局部的导数会很大。由于自变量是可大可小的,所以就需要参数足够大。那么避免过度拟合,减小参数,也就是减少权重就可以了。(具体的证明过程作者并没有给出,网上也没有查到)
具体方法,是改进了一下成本函数:
其中C0是原始的成本函数,λ是正则化参数,λ>0。后面那个求和是对整个神经网络中的权重w的平方求和。
对于二次成本函数:
对于交叉熵成本函数:
所以接下来的推导就比较简单了,先求∂C/∂w和∂C/∂b:
那么对于Δw和Δb:
与原来不使用正则化时的Δw相比,由于ηλw/n明显是大于0的,所以每次的w都要比原来减少的多,也就使得在使用了正则化的神经网络和不使用的相比,w都要小一些。(这里有一个w>0的前提,作者没有提到。不过其实想想w表示权重,好像一般也不取负值。另外w的初始值是使用正态分布随机取得的,也没有负值,所以这个前提作者没提,就暂时这么默认吧)
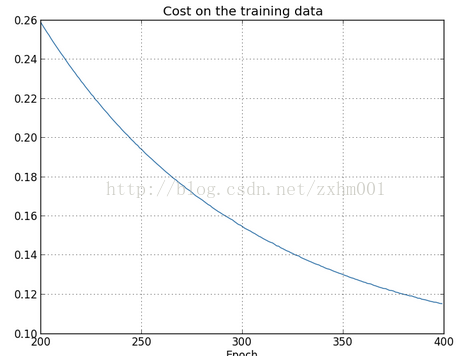
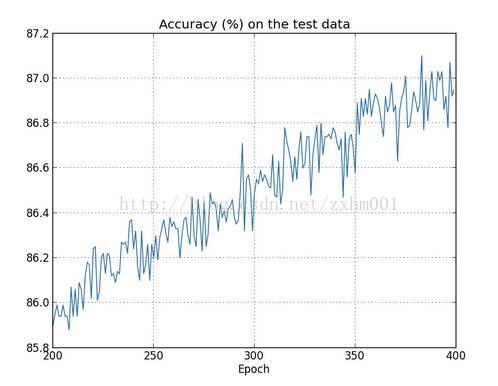
至于效果如何嘛:照样只选择1000个训练数据,照样训练400周期λ取值0.1,得到的C的变化图和对测试数据识别率的变化图如下:
欢迎关注我的微信公众号获取最新文章:










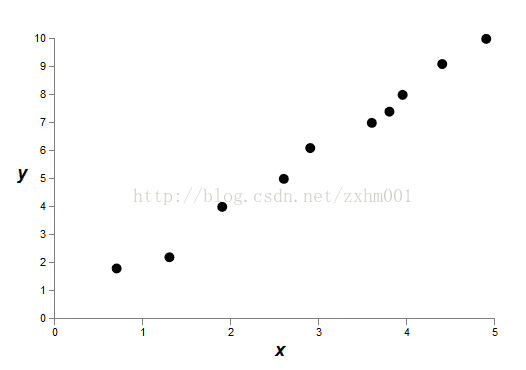
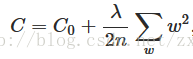
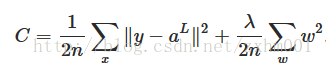
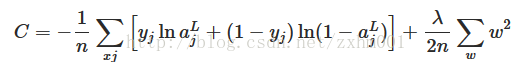
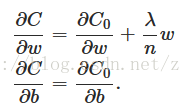
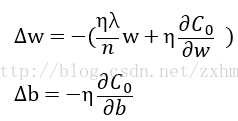














 3200
3200

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








