三支决策（从粗糙集说起）

初步了解

1. 是什么

首先，二支决策是什么？是用“非黑即白”的理念对一个事物进行判定的策略
（例如，如果投递的期刊在决定“是否录用的你论文”这个问题上采取的是二支决策，那么，论文发表的过程就不会那么长了。当你第一次提交文章时，编辑部就会决定，ok（马上接收发表）或者no（不行））

实际上，文章从投稿到接收得花一定的时间，需要根据审稿意见进行修改或作出解释，经过修改达到要求后才会被接收。这正是三支决策思想的体现，将不确定的事物放进“待定区”，且不立马作出决定，在得到更多的依据和支撑后再进行判断，从而避免直接接受或拒绝带来的风险。

2. 与粗糙集的关系（历史）

入门一个领域，应该先对这个领域的历史稍微做些了解：

1. 粗糙集的概念由Pawlak 于1982年提出于Rough sets 一文
2. 加拿大里贾纳大学的姚一豫教授于1989年将贝叶斯风险决策引入粗糙集中，提出了决策粗糙集理论
3. 姚一豫教授于2009年提出了三支决策理论，并指出三支决策的概念最初是由解释概率粗糙集的三个区域的需要引入的
4. 从2010年开始三支决策领域初步形成，学术界开始了三支决策方法的系统理论研究 姚一豫(2010)，姚一豫(2011)， 姚一豫(2012)
5. 2010-2013年国内先后出版了《决策粗糙集理论及其研究进展》、《三支决策理论与应用》和《三支决策与粒计算》三本专著来介绍三支决策的理论方法和实际应用
6. 此处为三支决策研究者提供了一个信息共享和交流的平台，其中汇总了致力于三支决策领域的学者们这些年的研究成果

三支决策是概率粗糙集语义的自然扩展，它的提出为粗糙集理论和决策理论的融合，以及粗糙集理论在实际决策问题中的应用建立起一座桥梁。（引自：刘盾等人，粗糙集理论：基于三支决策视角）

也就是说，三支决策是基于粗糙集的研究，但这个领域的学者们希望三支决策今后的研究不应完全局限于粗糙集，正致力于同其他学科和领域紧密联合。

3. 三支决策的形式化描述（定义）

设 U = { x 1 , . . . , x n } U=\{x_1,...,x_n\} U={x1​,...,xn​} 是有限、非空实体（对象）集， $C$是有限条件集。
定义：三支决策是基于条件集 $C$ ，通过映射 $f$ 将实体集 $U$ 划分为三个两两互不相交的R-域、L-域和-M域的过程（一般称为：正域、负域和边界域）：
U → f { L , M , R } U \xrightarrow{f}\{L,M,R\} Uf ​{L,M,R}

三支决策方法的重要元素 ：

1. 实体的评价函数（决策函数）：它的值称为决策状态值，其大小反应了实体的好坏程度
   【目前研究人员一般选择基于全序关系¹集合的评价函数，比较流行的是以$([0,1],⩽)$为代表的全序关系集合】
2. 阈值

有了决策状态值和阈值就能将所有实体划分到三个域中，即正域、负域和边界域。基于这三个域可以构造相应的三支决策规则：对于落在正域、负域和边界域的实体，分别使用接受、拒绝和不承诺规则。

4. 三支决策研究的主要问题

1. 评价函数值域的构造和解释：在三支决策理论中，评价函数用于对实体的状态进行估计和比较，某实体评价函数的取值代表了实体满足条件集C的程度，并且其取值应该是具有可比性的。通常情况下，可以在实体评价函数的值域上建立某种序关系。例如全序集（整数、实数集合、有限个等级…），也可以是偏序集和格。
2. 需要考虑评价函数的构造和解释。实体评价函数的构造根据具体应用而有所不同，如代价、风险、错误、利润、效益、用户满意度、投票等，同时也应考虑条件集合C。

---

深入了解

1. 从“粗糙集是什么”说起

粗糙集理论，是继概率论、模糊集、证据理论之后的又一个处理不确定性的数学工具。作为一种较新的软计算方法，粗糙集近年来越来越受到重视，其有效性已在许多科学与工程领域的成功应用中得到证实，是当前国际上人工智能理论及其应用领域中的研究热点之一。1982年，波兰数学家Z.Pawlak发表了经典论文Rough Sets，意味着粗糙集理论的诞生。

— 百度百科

2. 经典的Pawlak粗糙集

Pawlak粗糙集采用可定义集来近似说明不确定性概念。

假设 $U$ 是一个有限的非空子集，$R\subseteq U\times U$为论域 $U$ 上的一个等价关系²，即 $R$ 具有自反性、对称性和传递性。 $U$ 可以通过该等价关系 $R$ 划分成互不相交的子集，形成论域 $U$ 上的一个划分³。并且，将包含对象 $x$ 的等价类⁴标记为 [ x ] R = [ x ] = { y ∈ U ∣ x E y } [x]_R=[x]=\{y\in U |xEy\} [x]R​=[x]={y∈U∣xEy}。 $R$ 的所有等价类组成的集合称为由 $R$ 产生的商集⁵（其实就是 $U$ 的一个划分），记为 $U/R$ 。对于 $A\subseteq U$ ，$A$ 的上下近似定义为： a p r ‾ ( A ) = { x ∈ U ∣ [ x ] ∩ A ≠ ∅ } = { x ∈ U ∣ ¬ ( [ x ] ⊆ A c ) } \overline{apr}(A) = \{x\in U|[x]\cap A \ne \varnothing \} = \{x\in U|\lnot([x]\subseteq A^c) \} apr​(A)={x∈U∣[x]∩A​=∅}={x∈U∣¬([x]⊆Ac)} a p r ‾ ( A ) = { x ∈ U ∣ [ x ] ⊆ A } \underline{apr}(A) = \{x\in U|[x]\subseteq A\} apr​(A)={x∈U∣[x]⊆A}
举个栗子：

上图是一个常见的粗糙集图示，其中每一个方块表示已知的知识。将能用一个或几个方块开表示的知识结合称作确定集，而无法用这些方块组成的划分直接表示的知识集合称作粗糙集。图中不规则的近似圆形区域则为一个粗糙集（记为A），A的外围粗黑线围成的区域及中间的“T”型区域，是最接近该粗糙集的确定集，则将它们分别成为该粗糙集的上近似与下近似。

基于上下近似的定义，Pawlak粗糙集中的正域、负域和边界域表示为：
P O S ( A ) = a p r ‾ ( A ) = { x ∈ U ∣ [ x ] ⊆ A } POS(A) = \underline{apr}(A) = \{x\in U|[x]\subseteq A\} POS(A)=apr​(A)={x∈U∣[x]⊆A} N E G ( A ) = U − a p r ‾ ( A ) = { x ∈ U ∣ [ x ] ⊆ A c } NEG(A) = U - \overline{apr}(A) = \{x\in U|[x]\subseteq A^c\} NEG(A)=U−apr​(A)={x∈U∣[x]⊆Ac} B N D ( A ) = a p r ‾ ( A ) − a p r ‾ ( A ) = { x ∈ U ∣ ¬ ( [ x ] ⊆ A c ) ∧ ¬ ( [ x ] ⊆ A ) } = ( P O S ( A ) ∪ N E G ( A ) ) c BND(A) = \overline{apr}(A) - \underline{apr}(A) = \{x\in U|\lnot([x]\subseteq A^c) \land \lnot([x]\subseteq A)\} = (POS(A) \cup NEG(A))^c BND(A)=apr​(A)−apr​(A)={x∈U∣¬([x]⊆Ac)∧¬([x]⊆A)}=(POS(A)∪NEG(A))c

因此，在基于经典的Pawlak粗糙集表示的三支决策中，接受是因为条件$[x]\subseteq A$为真，拒绝是因为$[x]\subseteq A^c$为真。当对象既不能确定在正域，也不能确定在负域时，这就是一个非承诺决策。这里的正域POS就是R-域，负域NEG就是L-域。边界域BND就是M-域。

3. 概率粗糙集

对于$A\subseteq U$，给定一对阈值$(\alpha ,\beta ),0\le \beta <\alpha \le 1$ ，概率粗糙集$(\alpha ,\beta )$-上下近似集可定义为： a p r ‾ ( α , β ) ( A ) = { x ∈ U ∣ P r ( A ∣ [ x ] ) ≥ α } \underline{apr}_{(\alpha, \beta)}(A) = \{x\in U|Pr(A|[x]) \ge \alpha\} apr​(α,β)​(A)={x∈U∣Pr(A∣[x])≥α} a p r ‾ ( α , β ) ( A ) = { x ∈ U ∣ P r ( A ∣ [ x ] ) > β } \overline{apr}_{(\alpha, \beta)}(A) = \{x\in U|Pr(A|[x]) > \beta\} apr​(α,β)​(A)={x∈U∣Pr(A∣[x])>β}

选择分类的条件概率$Pr(A|[x])=|[x]\cap A|/|[x]|$作为评估函数，$|\cdot |$表示集合中元素的基数。根据三支决策定义可知，对于$A\subseteq U$ 可构造出如下基于粗糙集表示的三支决策：
P O S ( α , β ) ( A ) = { x ∈ U ∣ P r ( A ∣ [ x ] ) ≥ α } POS_{(\alpha, \beta)}(A) = \{x\in U|Pr(A|[x]) \ge \alpha\} POS(α,β)​(A)={x∈U∣Pr(A∣[x])≥α} N E G ( α , β ) ( A ) = { x ∈ U ∣ P r ( A ∣ [ x ] ) ≤ β } NEG_{(\alpha, \beta)}(A) = \{x\in U|Pr(A|[x]) \leq \beta\} NEG(α,β)​(A)={x∈U∣Pr(A∣[x])≤β} B N D ( α , β ) ( A ) = { x ∈ U ∣ β < P r ( A ∣ [ x ] ) < α } BND_{(\alpha, \beta)}(A) = \{x\in U|\beta < Pr(A|[x]) < \alpha\} BND(α,β)​(A)={x∈U∣β<Pr(A∣[x])<α}

可以看出，$\alpha =1,\beta =0$ 时，概率粗糙集退化成Pawlak粗糙集。

基于Pawlak粗糙集与概率粗糙集的三支决策比较分析：

Pawlak粗糙集：对于接受和拒绝的条件都过于严厉，只有完全被正确分类的元素才归到正域里，或只有完全错误的元素才归到负域里；这样定义的结果使得边界域达到最大。这种定义方式完全不考虑分类过程中的错误和模型的容错率，在实际中往往难以应用。

概率粗糙集：利用两个参数α和β来划分三个边界，决策者可以根据问题本身来给定合适的阈值，其决策过程也更为灵活和合理。然而，大多数概率粗糙集中，α和β的取值都是人为给定的，它们并没有回答为什么要这样设定。姚一豫教授在20世纪90年代初将贝叶斯决策理论引入到概率粗糙集中，提出决策粗糙集理论，很好地回答了这个问题。

4. 决策粗糙集

对于两状态的II类问题，实体有两种状态，即满足或不满足给定条件。当掌握信息不确定或不完整时，无法准确判断实体是否满足给定条件，只能通过实体的评价函数进行估计。决策粗糙集理论，以实体 $x$ 满足或不满足条件 $C$ 的概率作为评价函数，通过代价风险分析给出求解最优$(\alpha ,\beta )$值的方法。

两个重要元素：

1. 状态集： Ω = { X , ¬ X } \Omega=\{X,\lnot X\} Ω={X,¬X} 分别表示满足条件$C$和不满足条件$C$的实体集
2. 行动集： A = { a P , a B , a N } A=\{a_P,a_B,a_N\} A={aP​,aB​,aN​} 分别表示接受某事件、延迟决策和拒绝某事件的三种行动

最优$(\alpha ,\beta )$值的推导过程：

采取不同的行动会产生不同的损失，记 ${\lambda }_{PP},{\lambda }_{BP},{\lambda }_{NP}$ 分别表示当$x$满足条件$C$时，采取行动 $a_P,a_B,a_N$ 的损失；同理，记 ${\lambda }_{PN},{\lambda }_{BN},{\lambda }_{NN}$ 分别表示当$x$不满足条件$C$时，采取行动 $a_P,a_B,a_N$ 的损失。（如下表所示）

同时，以实体满足条件$C$的概率作为评价函数，记为$P(X|[x])$。且设风险函数$R(\Delta |x)$为决策动作$\Delta$的风险的数学期望（$\Delta$表示对 $x$ 的决策动作）。

因此，采取行动 $a_P,a_B,a_N$的相应风险估计（即期望损失）分别表示为：
接受的风险：$R(a_P|[x])={\lambda }_{PP}P(X|[x])+{\lambda }_{PN}(1-P(X|[x]))$
延迟决策的风险：$R(a_B|[x])={\lambda }_{BP}P(X|[x])+{\lambda }_{BN}(1-P(X|[x]))$
拒绝的风险：$R(a_N|[x])={\lambda }_{NP}(X|[x])+{\lambda }_{NN}(1-P(X|[x]))$
[$P(X|[x])+P(\neg X|[x])=1$]

根据贝叶斯决策准则，需要选择期望损失最小的行动集作为最佳行动方案，于是有三条决策规则（Ｐ），（Ｂ），（Ｎ）：
接受（P）：当满足$R(a_P|[x])\le R(a_B|[x])$ 且 $R(a_P|[x])\le R(a_N|[x])$
延迟（B）：当满足$R(a_B|[x])\le R(a_P|[x])$ 且 $R(a_B|[x])\le R(a_N|[x])$
拒绝（N）：当满足$R(a_N|[x])\le R(a_P|[x])$ 且 $R(a_N|[x])\le R(a_B|[x])$

考虑到两个合理的假设：

1. 接受正确事物的损失不大于延迟接受正确事物的损失，且这两者都小于拒绝正确事物的损失
2. 拒绝错误事物的损失不大于延迟拒绝错误事物的损失，且这两者都小于接受错误事物的损失

因此对应产生不等关系：

1. $0\le {\lambda }_{PP}\le {\lambda }_{BP}\le {\lambda }_{NP}$
2. $0\le {\lambda }_{NN}\le {\lambda }_{BN}\le {\lambda }_{PN}$

把采取行动 $a_P,a_B,a_N$的相应风险估计$R(a_P|[x]),R(a_B|[x]),R(a_N|[x])$ 代入表示三条决策规则的不等式中，化简后则有下表所示结果：

为了更简洁地表达，有：
$$\alpha =\frac{({\lambda }_{PN}-{\lambda }_{BN})}{({\lambda }_{PN}-{\lambda }_{BN})+({\lambda }_{BN}-{\lambda }_{PP})}$$$$\beta =\frac{({\lambda }_{BN}-{\lambda }_{NN})}{({\lambda }_{BN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{PP})}$$$$\gamma =\frac{({\lambda }_{PN}-{\lambda }_{NN})}{({\lambda }_{PN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{PP})}$$

且由表中规则(B)可知，$\alpha >\beta$，简单化简则有：
$$\frac{{\lambda }_{BP}-{\lambda }_{PP}}{{\lambda }_{PN}-{\lambda }_{BN}}<\frac{{\lambda }_{NP}-{\lambda }_{BP}}{{\lambda }_{BN}-{\lambda }_{NN}}$$

此外，由不等式$\frac{b}{a}>\frac{d}{c}\Rightarrow \frac{b}{a}>\frac{b+d}{a+c}>\frac{d}{c}$(a,b,c,d > 0)，则有：
$$\frac{{\lambda }_{BP}-{\lambda }_{PP}}{{\lambda }_{PN}-{\lambda }_{BN}}<\frac{{\lambda }_{NP}-{\lambda }_{PP}}{{\lambda }_{PN}-{\lambda }_{NN}}<\frac{{\lambda }_{NP}-{\lambda }_{BP}}{{\lambda }_{BN}-{\lambda }_{NN}}$$所以，$0\le \beta <\gamma <\alpha \le 1$成立。因此，三条决策规则可以重写为：
接受（P）：当满足$P(X|[x])\ge \alpha$
延迟（B）：当满足$\beta <P(X|[x])<\alpha$
拒绝（N）：当满足$P(X|[x])\le \beta$

基于决策粗糙集的三支决策中最佳$(\alpha ,\beta )$值为：
$$\alpha =\frac{({\lambda }_{PN}-{\lambda }_{BN})}{({\lambda }_{PN}-{\lambda }_{BN})+({\lambda }_{BN}-{\lambda }_{PP})}$$$$\beta =\frac{({\lambda }_{BN}-{\lambda }_{NN})}{({\lambda }_{BN}-{\lambda }_{NN})+({\lambda }_{NP}-{\lambda }_{PP})}$$

---

参考：
于洪. 三支决策：复杂问题求解方法与实践[M]. 科学出版社, 2015.
祝宏玉. 基于不确定性的代价敏感半监督学习[D]. 深圳大学, 2018.
刘盾, 李天瑞, 李华雄. 粗糙集理论：基于三支决策视角[J]. 南京大学学报(自然科学), 2013, 49(5):574-581.
刘盾. 三支决策与粒计算[M]. 科学出版社, 2013.
屈婉玲. 离散数学及其应用[M]. 2011.

---

补充数学概念

---

1. 全序关系：
   
   核心：强调一个集合是全序集合，则是在强调该集合的任意两个元素之间都具有可比性。
   具体：请配合离散数学教材食用
   （本人从图书馆扛了四本书分别是：《离散数学极其应用》(屈婉玲，高等教育出版社)、《离散数学(第三版)》(屈婉玲，清华大学出版社)、《三支决策与粒计算》(刘盾，科学出版社）、《三支决策：复杂问题求解方法与实践》） ↩︎

2. 等价关系：
   
   例：
   设 A = { 1 , 2 , . . . , 8 } A=\{1,2,...,8\} A={1,2,...,8}，如下定义 $A$ 上的关系 $R$：
   R = { < x , y > ∣ x , y ∈ A ∧ x ≡ y ( m o d   3 ) } R=\{<x,y>|x,y\in A \wedge x \equiv y(mod \ 3)\} R={<x,y>∣x,y∈A∧x≡y(mod 3)}其中$x\equiv y(mod3)$称为 $x$ 与 $y$ 模3相等，即 $x$ 除以 $3$ 的余数与 $y$ 除以 $3$ 的余数相等。通过上述定义可知， $R$ 是 $A$ 上的等价关系，且该关系的关系图为：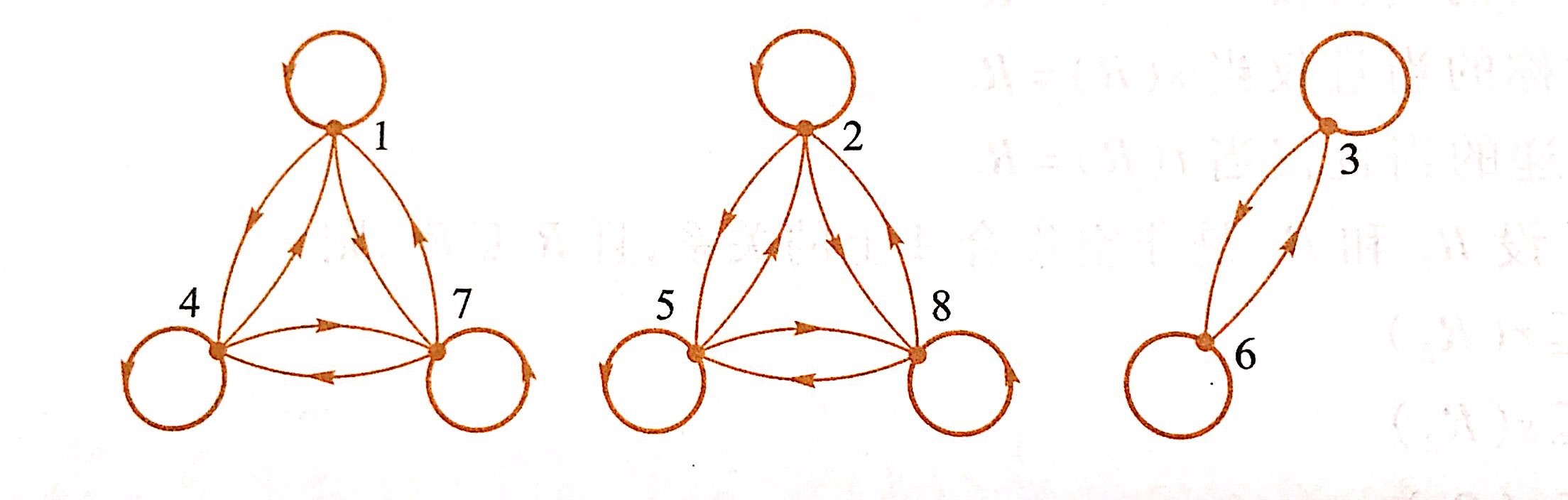

   
   
   可以看出上述关系图被分为3个互不联通的部分，其中每部分的数两两都有关系，而不同部分的数则没有关系，每一部分中所有定点构成一个等价类。 ↩︎

3. 划分
   设A为非空集合，若A的子集族$\pi (\pi \subseteq P(A)$，是$A$的子集构成的集合$)$满足下面的条件：
   1）$\varnothing \notin \pi$
   2）$\forall x\forall y(x,y\in \pi \wedge x\ne y\to x\cap y=\varnothing )\notin \pi$ (式中 $\ne$是不等号，我也不知道为啥会编译成这样…)
   3）$\cup \pi =A$ ($\cup \pi$ 为 $\pi$ 的广义并：即 $\pi$ 中元素的元素构成的集合称为 $\pi$ 的广义并)
   则称 $\pi$ 是 $A$ 的一个划分，称 $\pi$ 中的元素为 $A$ 的划分块。
   例如， A = { 1 , 2 , 3 } A=\{1,2,3\} A={1,2,3}的所有划分如下所示：

   
   
   比较商集与划分的定义可知，商集就是A的一个划分，且不同的商集将对应于不同的划分。
   反过来，任给 $A$ 的一个划分$\pi$ ，如下定义 $A$ 上的关系 $R$ ： R = { < x , y > ∣ x , y ∈ A ∧ x 与 y 在 π 的 同 一 个 划 分 块 中 } R=\{<x,y>|x,y\in A \wedge x 与 y 在\pi的同一个划分块中\} R={<x,y>∣x,y∈A∧x与y在π的同一个划分块中}则不难证明 $R$ 为 $A$ 上的等价关系，且该等价关系所确定的商集就是 $\pi$ 。
   由此可见， $A$ 上的等价关系与 $A$ 的划分是一一对应的。 ↩︎

4. 等价类
   设 $R$ 为非空集合 $A$ 上的等价关系，$\forall x\in A$，令：
   [ x ] R = { y ∣ y ∈ A ∧ x R y } [x]_R = \{y|y\in A \wedge xRy\} [x]R​={y∣y∈A∧xRy}称 $[x{]}_R$ 为 $x$ 关于 $R$ 的等价类，简称为 $x$ 的等价类，简记为 $[x]$ 或 $\overline{x}$。
   对于等价关系的介绍中所举的例子，等价类是：
   [ 1 ] = [ 4 ] = [ 7 ] = { 1 , 4 , 7 } [1]=[4]=[7]=\{1,4,7\} [1]=[4]=[7]={1,4,7} [ 2 ] = [ 5 ] = [ 8 ] = { 2 , 5 , 8 } [2]=[5]=[8]=\{2,5,8\} [2]=[5]=[8]={2,5,8} [ 3 ] = [ 6 ] = { 3 , 6 } [3]=[6]=\{3,6\} [3]=[6]={3,6} ↩︎

5. 商集
   设 $R$ 为非空集合 $A$ 上的等价关系，以 $R$ 的所有等价类作为元素的集合称为 $A$ 关于 $R$ 的商集，记作 $A/R$，即： A / R = { [ x ] R ∣ x ∈ A } A/R=\{[x]_R|x\in A\} A/R={[x]R​∣x∈A}例如，等价关系的介绍中所举的例子，商集是： { { 1 , 4 , 7 } , { 2 , 5 , 8 } , { 3 , 6 } } \{\{1,4,7\},\{2,5,8\},\{3,6\}\} {{1,4,7},{2,5,8},{3,6}} ↩︎