图论填坑系列TAT

这篇文章禁止以任何形式转载。
这篇文章禁止以任何形式转载。
这篇文章禁止以任何形式转载。

---

dij我现在还不会我会说嘛……
虽然说暂时死不了。
Tarjan算法
首先我们要知道这个东西可以把有向图缩掉强连通分量后变成DAG。
有向图强连通分量：在有向图G中，如果两个顶点vi,vj间（vi>vj）有一条从vi到vj的有向路径，同时还有一条从vj到vi的有向路径，则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。有向图的极大强连通子图，称为强连通分量(strongly connected components)。
简而言之，有向图的强连通分量就是环嘛。
我们考虑一个DAG的dfs搜索树。
对点进行标号，我们会发现，如果一个点可以访问到已经标号过的点，那么这个点显然可以回溯到某个子树的根节点。
让我们来冷静思考一下，其实就是这样：

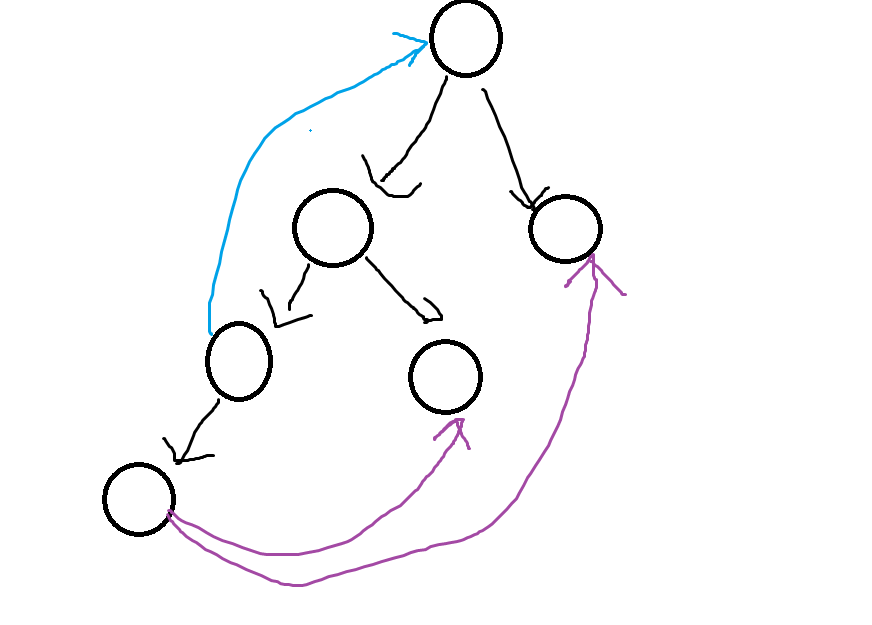
发现一个问题：
1.紫色的边显然和这个节点不是双联通的。
2.蓝色的边才是。
啊……我数学不好，其实是两个问题hhh
发现，实际上我们紫色的边是横叉边，（管它怎么叫呢）即，虽然可以返回深度更浅的地方，但是实际上它并不是强联通的。
我们发现，只有指向已经压入dfs过程中的栈的点的这种边才是证明强联通的根据。
而且，不仅如此，我们还发现一些性质：
如果u是v的父亲，v可以返回v的某个父亲，那么u也必然能返回这个节点。
如果u是v的父亲，v可以返回u的某个祖先，那么u能返回的节点v也同样可以返回。
我们知道的一点是，如果某个节点x可以返回其祖先y，那么x和y是强联通的。
更进一步讲，如果某个节点x可以返回其祖先y，那么$y->x$这一段路径都是强联通的。
仔细想一想，我们如果想知道u向搜索树往下走可以返回的最浅祖先，那么我们就对其子树进行计算然后取标号最小的即可。
但是我们遇到一个问题。

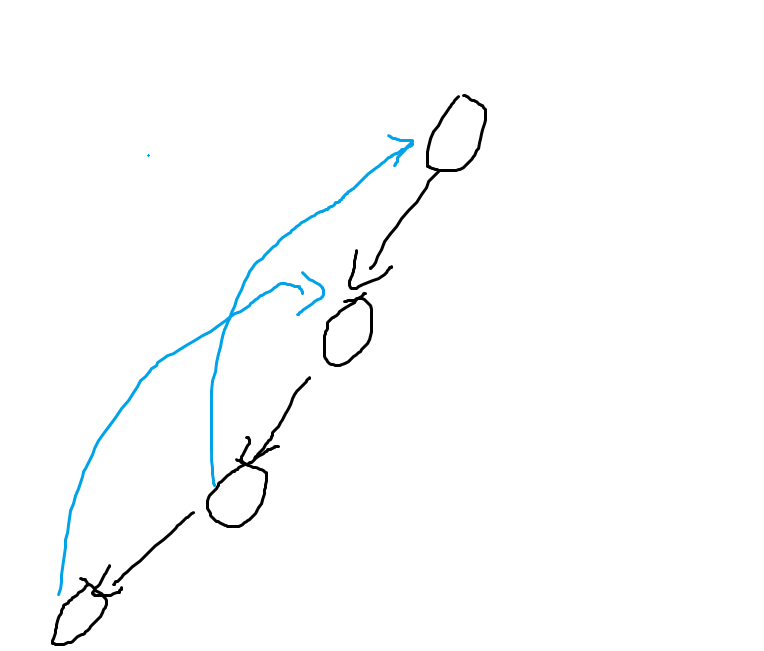
如图所示的情况，我们这四个点显然是强连通的。
仔细思考后，我们知道每个强连通分量必然是有一个根的，我们可以看出的一点是，如果一个节点的可回溯祖先节点就是它本身的话，那么这个节点必然无法再向上回溯，即这个点单独属于一个强连通分量。
我们只需要在dfs的过程中记录如下信息即可：
1.dfs序及编号最早的回溯节点
2.属于哪个scc

void dfs(int x)
{
    dfn[stk[++ tp] = x] = low[x] = ++ tim;
    RepG(i,x)
    {
        if(!dfn[v])dfs(v),low[x] = min(low[v],low[x]);
        else if(!bel[v])low[x] = min(dfn[v],low[x]);
    }
    if(dfn[x] == low[x])
    {
        int y;++ scc;
        do{bel[y = stk[tp --]] = scc;}while(y != x);
    }
}

这个是有向图的强连通分量的知识。

---

接下来强调一个点双联通。
对于一个连通图，如果任意两点至少存在两条点不重复路径，则称这个图为点双连通的.（简称双连通）点双联通分量就是极大点双联通子图。
想一想之后可以画出三元环什么的……
然后画出了一个”8”字形。
(就是上面一个三角底下一个三角共顶点)
请注意，这个图并不是点双联通，因为对于上下两个三角的点，只有一条经过中间点的路径T_T
所以说啊……
点双连通图的定义等价于任意两条边都同在一个简单环中。
感性认（民）识（科）一下，觉得就是对的吧……
不(会)证明了……
那么我们来想想，如果两个子图并不是点双联通的，有什么特别的事情么？
显然：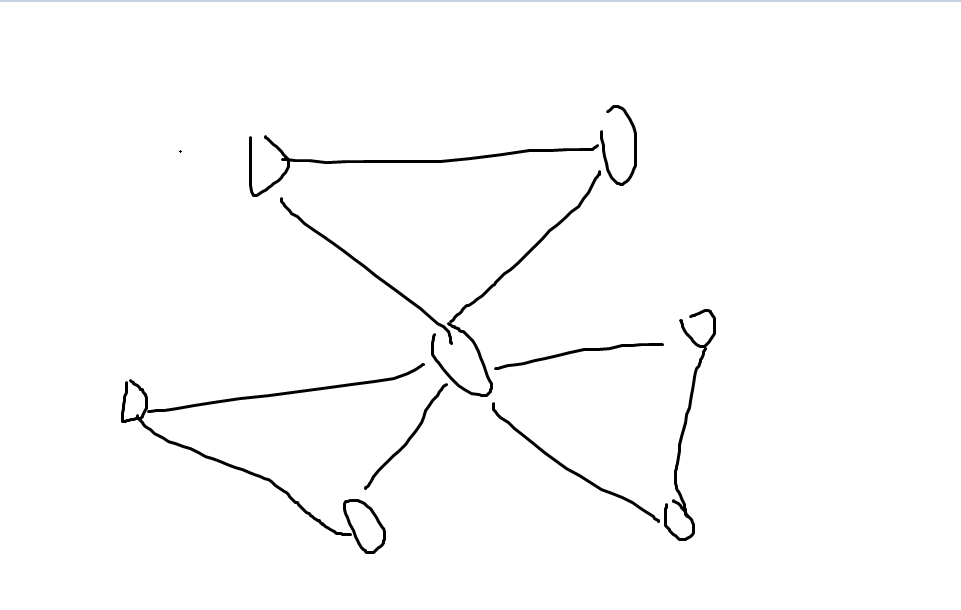
对于这个和diep里面某些tank很像的图片，对三角形进行逆时针标号。
我们发现，中间的这个点：
三角形1<->三角形2要经过这个点。
三角形1<->三角形3要经过这个点。
三角形2<->三角形3要经过这个点。
真是痛苦呢，要被这么多人踩哈哈哈哈哈
我们定义割点：删去这个点及其伸出的边之后，原图是不联通的。
我们可以发现，只有中间的点是割点。

================================================

注意，以下是求解割点部分，和点双联通分量虽有关系，但是暂时关系不大。
我们可以先忘掉之前点双联通分量的定义，专心来看怎么求解割点。
考虑无向图的dfs搜索树（也是一个点只遍历一遍），发现：
1.当根节点的子树数目>1的时候，根节点是割点。
2.对于非根节点u，如果存在一个节点v，使得v能返回的最早节点是u子树中的点(含u)。
关于这个东西的证明：
1是显然的。
对于2：

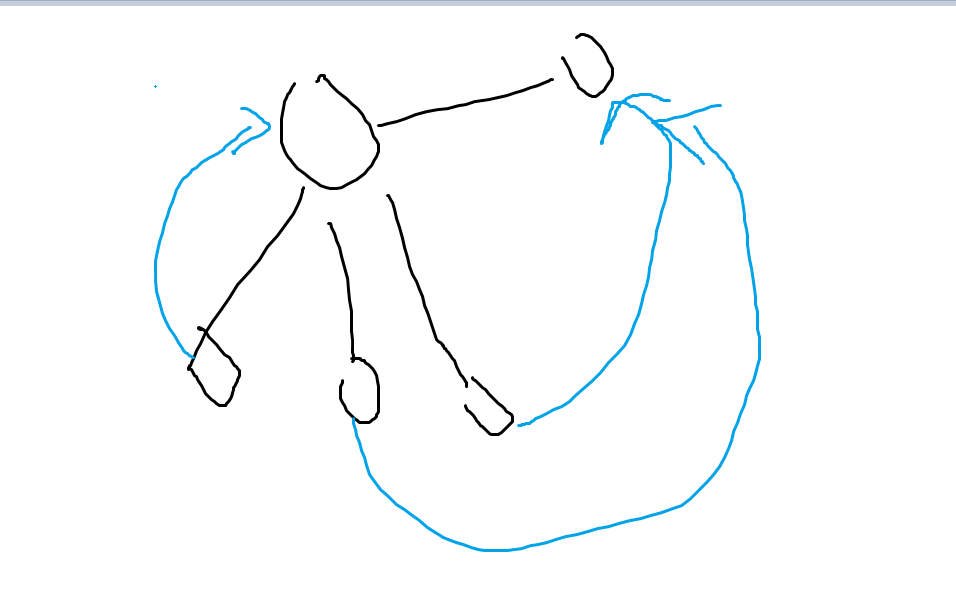
我们删掉那个最大个的节点之后，会发现这个节点的最左侧的儿子不联通。
实际上也是显然的，对吧。

void dfs(int x,int fa = -1)
{
    dfn[x] = low[x] = ++ tim;
    int idx = 0;
    RepG(i,x)
    {
        if(!dfn[v])
        {
            idx ++;
            dfs(v,x);
            low[x] = min(low[v],low[x]);
            if(low[v] >= dfn[x])
                isc[x] = 1;
        }
        else if(dfn[v] < dfn[x] && v != fa)
            low[x] = min(low[x],dfn[v]);
    }
    if(idx == 1 && x == Root)isc[x] = 1;
}

==================================================

我们终于可以正式进入求解点双的部分了。
我们发现，割点会存在于多个点双中，但是边只会存在某个点双中。
记录点双的数目是bcc。
在dfs的过程中记录边是否入栈。
考虑到割点会被重复计入，我们额外记录数组表示bcc时间戳就好了。

void dfs(int x,int fa = -1)
{
    int idx = 0,y;
    dfn[x] = low[x] = ++ tim;
    RepG(i,x)
    {
        if(v == fa)continue;
        if(!dfn[v])
        {
            idx ++;
            stk[++ scnt] = i;
            dfs(x,v);
            low[x] = min(low[v],low[x]);
            if(low[v] >= dfn[x])
            {
                isc[x] = 1;
                bel[++ bcc].clear();
                do
                {
                    y = stk[tp --];
                    if(bccno[edge[y].a] != bcc)
                    {
                        bel[bcc].push_back(edge[y].a);
                        bccno[edge[y].a] = bcc;
                    }
                    if(bccno[edge[y].b] != bcc)
                    {
                        bel[bcc].push_back(edge[y].b);
                        bccno[edge[y].b] = bcc;
                    }
                }while(edge[y].a != x || edge[y].b != v);
            }
        }
        else if(dfn[v] < dfn[x])
        {
            low[x] = min(low[x],dfn[v]);
            stk[++ tp] = i;
        } 
    }
    if(x == Root && idx > 1)isc[x] = 1;
}

写的好蛋疼啊……
这样我们就可以知道有几个点双辣！

===========================================

桥：一条边称为桥（或者割边）当且仅当去掉该边之后的子图不连通。
我们仔细思考一下，就能明白，当存在一条边满足：
$low[v] > dfn[u]$的时候我们就可以确定(u -> v)是桥了。
边双联通分量：
如果任意两点至少存在两条边不重复路径，则称该图为边双连通的。
边双连通的极大子图称为边双连通分量。
如果有k个桥，那么显然有(k+1)个边双。
怎么求解边双呢？
自然是只要遇到一个dfn[x] == low[x]的地方，那么就把这坨东西全都缩到一个边双利就好辣！
注意重边的判断！

void dfs(int x,int fa = -1)
{
    low[x] = dfn[stk[++ tp] = x] = ++ tim;
    RepG(i,x)
    {
        if((i ^ 1) == fa)continue;
        if(!dfn[v])
        {
            dfs(v,i);
            low[x] = min(low[v],low[x]);
            if(dfn[v] == low[v])isb[i] = 1;
        }
        else if(!bel[v])low[x] = min(dfn[v],low[x]);
    }
    if(dfn[x] == low[x])
    {
        scc ++;
        int y ;
        do{y = stk[tp -- ];bel[y] = scc;}while(x != y);
    }
}

GTMD,tarjan这个大坑终于被我填了。。。。
接下来必须填网络流和费用流的坑……
拆点什么的思想现在完全没有……
需要好好♂培♂养♂一下。