二叉树（BST树）内结点的删除（3种情况全解）

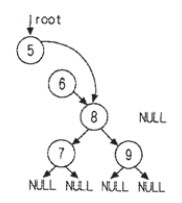
现在有一棵二叉树查找树如下：

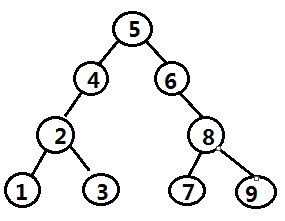
如果我们需要删除一个结点，而且在删除之后，依然满足二叉查找树的数据排序策略。此时删除操作可分为一下三种情况。如下

---

情况1：结点没有左子树
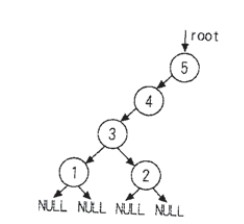
如图：一棵没有左子树的二叉树

如果在此情况下删除结点，按照结点的位置又可以分为三种处理方式。如下

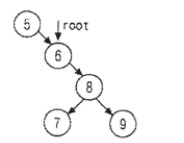
• 删除根结点：删除根结点也就是删除结点 5，此时只需将根结点指针指向其右子树结点。如下图
  

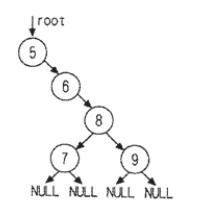
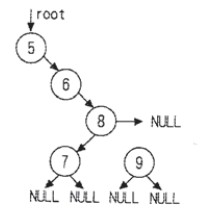
• 删除叶子结点：如果删除的结点是叶子结点也就是结点9，此时只需将父节点指向NULL，如下图
  

• 三处中间结点：如果删除的结点是中间结点也就是结点6，此时只要将父节点指向右子结点即可。如下图
  

---

情况2：结点没有右子树
如图：一棵没有右子树的二叉树

如果在此情况下删除结点，按照结点的位置也可以分为三种处理方式。它和上面将到的没有左子树的三种情况一样只是左右指针的差异。这里不做过多的赘述。大家自己理解一下。

---

情况3:结点具有左子树也有右子树
如图：如果二叉树是这种情况，其处理不会因为结点的位置不同而不同，但是处理过程就比较复杂。

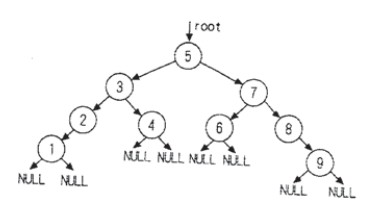
观察上述二叉树，如果需要删除根结点5，我们若能找到一个结点也就是结点3和7之间，然后将它取代根节点的位置。这样整棵二叉树并不需要太对的搬动就可以完成结点删除的操作。例如：结点4正符合上面的要求，等到删除结点5 后其结构如图

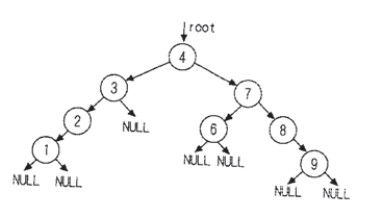
我们可以发现真正删除的结点是原来的结点4，然后将原来根结点的内容5替换为4，就完成了删除的操作，问题是如何找到符合条件的结点4，其实我们观察二叉查找树的特性：
其特性如下:

• 每一个结点的值都不同，也就是整棵树中的每一个结点都拥有不同的值
• 每一个结点的数据大于左子树结点（如果有的话）的数据，但是小于右子树的结点（如果有的话）的数据。
• 左右两部分的子树，也是一课二叉查找树。

如果想要删除结点后二叉树依然是一棵二叉查找树，可以发现符合这样要求的结点只有两个，那就是4和6.它们是从根结点5的左结点3一直从右子树走到叶子结点和右结点7一直往左子树走一直走到叶子结点。

现在我们使用从左子结点开始寻找替换的结点，如果删除的结点是5，就从结点5的左子结点3开始往右子树找，直到达到叶子结点，找到的是结点4。接着删除此结点，其方法和情况1,2相同，最后取代原结点5成为4。

如果删除的是结点3，此时左子结点2并没有右子结点，所以符合条件的就是结点2，删除的操作就是成为删除一个没有右子树的结点2，然后将原结点3的值取代成为2.其完整的操作如下图

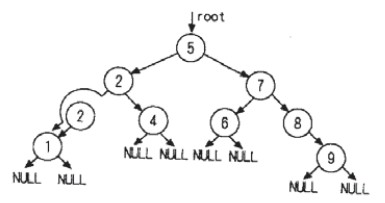
至于从右子结点开始寻找和替换删除结点值的方法，和从左边结点开始寻找类似…….

好，直接看代码

/*********************************************************
-  Copyright (C): 2016
-  File name    : deletetree.c
-  Author       : - Zhaoxinan -
-  Date         : 2016年08月05日 星期