🌞欢迎来到人工智能的世界
🌈博客主页：卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创！
📆首发时间：🌹2025年2月15日🌹
✉️希望可以和大家一起完成进阶之路！
🙏作者水平很有限，如果发现错误，请留言轰炸哦！万分感谢！
目录
简单运算
为啥要学习（整数或者是小数的四则运算）？
母亲一共给了 24 元零花钱，让小明和小红平均分着花，看看每个人能花多少钱？
小明走进了一家文具店，准备买学习用品。他看到：
一支铅笔 3 元 ✏️
一本笔记本 12 元 📖
一个橡皮 1元 🔲
他买了两个铅笔和一个橡皮一共多少钱？
他付 10 元，店员要找回多少？
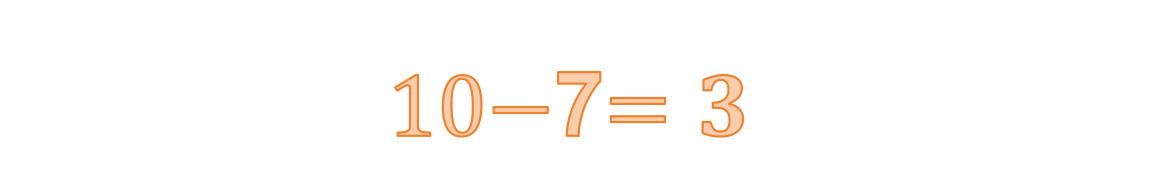
为啥要学习负数？
负数 - 正数 代表欠更多的钱，余额变小。
上午欠我3元，下午欠我2元，总共欠我多少钱？
负数 + 正数 代表挣钱，余额变大。
晚上你收到了10元的红包，你现在有多少钱？
为啥要学习绝对值？
绝对值表示的是数的大小，而不考虑方向，就是把正数不变，负数变成正数
集合
为啥要学习集合？
因为方便运算
集合（Set） 就是一群有共同特点的东西。
比如：
- 篮球队员的名单
- 1 到 10 之间的偶数
- 班级里喜欢数学的同学
这些东西都有个特点，就是它们可以被看作一个“整体”！
数学上，我们一般用 大括号 表示集合，比如：
✅ 1 到 10 之间的偶数：
{2,4,6,8,10}
✅ 小明有的玩具：
{汽车,飞机,机器人}
✅ 小华有的玩具：
{飞机,积木,机器人}
集合可以帮我们解决哪些问题？
✅ 去掉重复的东西 🧹
比如，你的文具盒里有：
{铅笔,橡皮,铅笔,尺子,橡皮}
如果我们用集合来表示，它就会自动去掉重复的部分：
{铅笔,橡皮,尺子}
集合不管有多少个一样的东西，它只算一个，这样就能帮我们整理数据！
✅ 找出共同的部分 👬
比如，小明和小华的玩具集合是：
- 小明的玩具：{汽车,飞机,机器人}
- 小华的玩具：{飞机,积木,机器人}
他们都有的玩具是什么？就是两个集合的交集：
{飞机,机器人}
这样，我们就可以轻松找出共同的东西啦！🎯
区间和不等式
为啥要学习区间？
区间（Interval）是一个表示范围的概念。
我们用区间来表示一个数值范围，这个范围可以是有限的，也可以是无限的。
比如一个女生找男朋友的标准。（可以用区间也可以用集合表示）
充分必要条件
充分条件 就是 如果这个条件成立，那么某件事情肯定成立。
举个例子：
“吃了冰淇淋，肚子就会疼”
这里“吃了冰淇淋”就是一个充分条件，因为只要你吃了冰淇淋，肚子疼就一定会发生。也就是
说，如果你吃了冰淇淋，肚子疼的事就一定会发生。
但这并不意味着肚子疼只会因为吃冰淇淋，可能还有别的原因。只是吃冰淇淋是够让你肚子疼的
条件。
肚子疼就是一个必要条件
结婚证是结婚的必要且充分条件
你结婚一定需要结婚证（必要条件），而且只要有了结婚证，结婚就算成了（充分条件）。
换句话说，结婚证既确保你结婚了（充分条件），又是必须要有的（必要条件）。
函数
在数学里，指数函数是这样的：我们有一个底数，然后把它不断乘自己，这个“次数”就叫做指数。
比如，假设我们有一个底数 2，如果我们让它重复乘自己多次，我们就得到了指数函数的结果。
用数学表示就是：
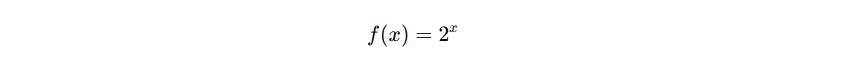
假设你有 2 个苹果，每天苹果的数量翻倍（每一天苹果的数量变成原来的2倍）。那会发生什么呢？
第一天你有 2 个苹果。
第二天，你的苹果数量就变成了 2 × 2 = 4 个。
第三天，你的苹果数量就变成了 4 × 2 = 8 个。
第四天，你的苹果数量又变成了 8 × 2 = 16 个。
向量
向量的定义为具有大小和方向的量。
研究对象：向量
向量是有方向的线段，线段的长度代表向量的大小，箭头代表向量的方向。
几何视角和坐标表示
现实视角
向量可以代表着一些信息
向量的大小
向量的内积
坐标视角
几何视角
从几何角度来看，向量内积与向量的长度和它们之间的夹角有关。具体地，两个向量的内积可以表示为：
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
