ACM数论模板（更新ing...）

• 埃氏筛法
• 欧拉筛法
• 拓展/欧几里得
• 线性同余方程
• 线性同余方程组
• 数论四大定理
• 欧拉函数
• 莫比乌斯函数
• 快速幂
• 矩阵快速幂
• 博弈论
• 生成排列
• 排列组合计数
• 鸽笼原理和容斥原理
• 生成函数

1、埃氏筛法
思想： 对于不超过n的每个非负整数p,删除2p,3p,4p…当处理完所有数之后，还没有被删除的就是素数。其时间复杂度为 O(N*loglogN)。

memset(vis,0,sizeof(vis));
for(int i=2;i<=n;i++){
    for(int j=2*i;j<=n;j+=i)vis[j]=1;
}

优化： 1. p限定为素数 2. 内层循环从i*i开始（i*2~i*(i-1)为重复删除） 3. n以内的合数的最小质因数一定不超过√n。

    memset(vis,0,sizeof(vis));
    int m=sqrt(n+0.5);
    for(int i=2;i<=m;i++){
        if(!vis[i]){
            for(int j=i*i;j<=n;j+=i)vis[j]=1;
        }
    }

区间筛法：给定整数a和b，请问区间[a,b]内有多少个素数？（a<b≤10¹², b-a≤10⁶）
思想：b以内的合数的最小质因数一定不超过√b，求√b以内的素数表同时将其倍数从[a,b]的表中划去。

bool v1[Max_n]; //√b以内的素数表
bool v2[Max_n];

int Prime(ll a,ll b){
    if(b<2)return 0;
    if(a<2)a=2;
    memset(v1,0,sizeof(v1));
    memset(v2,0,sizeof(v2));
    ll f=sqrt(b+0.5);
    for(ll i=2;i<=f;i++){
        if(!v1[i]){
            for(ll j=i*i;j<=f;j+=i)v1[j]=1;
            for(ll j=max(i*i,(a+i-1)/i*i);j<=b;j+=i)v2[j-a]=1;
            //((a+i-1)/i)*i是符合>=a最小是i倍数的数
        }
    }
    int k=0;
    for(int i=0;i<=b-a;i++){
        if(!v2[i])k++;
    }
    return k;
}

2、欧拉筛法
思想： 每个合数紧被它最小的质因数筛去。其时间复杂度为 O(N)。

int ans=0,pri[Max_n];
bool vis[Max_n];

void getpri(){
    memset(vis,0,sizeof(vis));
    for(int i=2;i<Max_n;i++){
        if(!vis[i])pri[ans++]=i;
        for(int j=0;j<ans;j++){
            if(i*pri[j]>=Max_n)break;
            vis[i*pri[j]]=1;
            if(i%pri[j]==0)break;  // 保证了每个合数紧被它最小的质因数筛去
        }
    }
}

3、扩展/欧几里得

描述： 设a,b和c为任意整数，对于不定方程组$ax+by=c$，如果c不是gcd(a,b)的倍数，则不定方程没有整数解；如果c是gcd(a,b)的倍数，则方程有无穷多整数解。若(x₀,y₀)是方程的一组整数解，则它的任意整数解都可以写成(x₀+kb’, y₀-ka’)，其中a’=a/gcd(a,b)，b’=b/gcd(a,b)，k取任意整数。

// 求整数x和y，使得ax+by=d,且|x|+|y|最小。其中d=gcd(a,b)
// 即使a,b在int范围内，x和y也有可能超出int范围

ll exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0){
        x=1,y=0;
        return a;
    }
    ll d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}

4、线性同余方程

线性同余方程： 形如ax≡b(mod m)的方程。a和b是整数，m是正整数，且gcd(a,m)=d。如果b%d≠0，则ax≡b(mod m)无解；如果b%d=0，则ax≡b(mod m)恰有d个模m不同余的解。所有的解可以表示为：x=x0+k*(m div d)。

模的逆元： 给定整数a，且gcd(a,m)=1,称ax≡b(mod m)的一个整数解为a模m的逆。

// 扩展欧几里得求解
ll exgcd(ll a,ll b,ll &x,ll &y){
    if(b==0){
        x=1,y=0;
        return a;
    }
    ll d=exgcd(b,a%b,y,x);
    y-=a/b*x;
    return d;
}

ll inverse(ll a,ll m){ // 求a模m的逆，不存在返回-1
    ll x,y;
    ll d=exgcd(a,m,x,y);
    if(d==1)return (x%m+m)%m;
    else return -1;
}

// 费马小定理求解
// 费马小定理：若p为素数，a为正整数，且gcd(a,p)=1，则有a^(p-1)≡1(mod p)。
// 那么a*a^(p-2)≡1(mod p)，则a^(p-2)是a模p的逆啦。

ll inverse(ll a,ll p){ 
    return quickMod(a,p-2,p);
}

5、线性同余方组

中国剩余定理： 设$m_1,m_2...m_k$是两两互质的正整数，则同余方程组

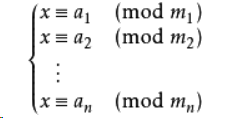
有模$M=m_1\ast m_2...\ast m_k$的唯一解。
解为$x\equiv (a_1{M}_1{M}_1^{-1}+a_2{M}_2{M}_2^{-1}+...+a_k{M}_k{M}_k^{-1})modM$，其中$M_i=\frac{M}{m_i}$，$M_i^{-1}$为$M_i$模$m_i$的逆元。

// n个方程：x≡a[i](mod m[i])  （互质的情况）
ll china(int n){
    ll M=1,ans=0;
    for(int i=0;i<n;i++)M*=m[i];
    for(int i=0;i<n;i++){
        ll w=M/m[i],x,y;
        exgcd(w,m[i],x,y);
        ans=(ans+a[i]*w*x)%M;
    }
    return (ans+M)%M;
}

// n个方程：x≡a[i](mod m[i])  （不互质的情况）
// 采用两两合并的思想：
// x=a1+m1*x1
// x=a2+m2*x2
// 合并为：x≡x'(mod lcm(m1,m2));

ll china(int n){
    ll m1=m[0],a1=a[0],x,y;
    for(int i=1;i<n;i++){
        ll m2=m[i],a2=a[i];
        ll d=exgcd(m1,m2,x,y);
        if((a2-a1)%d!=0)
            return -1;  // 无整数解
        x*=(a2-a1)/d;   // 得到一个特解x
        ll t=m2/d;
        x=(x%t+t)%t;    // 根据线性同余方程通解形式：x=x0+k*t，求出最小非负整数解x0
        a1=m1*x+a1;     // 代入x=a1+m1*x1
        m1=m1*t;        // m1=m1*m2/d;
    }
    if(a1==0)return m1;  //余数都为0
    return a1;
}

6、数论四大定理

威尔逊定理： 如果$p$是素数，则$(p-1)!\equiv -1(modp)$。
费马小定理： 如果$p$是素数，$a$是正整数，且$gcd(a,p)=1$，则$a^{p-1}\equiv 1(modp)$。
欧拉定理： 如果$a$和$n$是互素的正整数，则$a^{\phi (n)}\equiv 1(modn)$。
孙子定理： 即中国剩余定理。

7、欧拉函数

描述： 欧拉函数φ(n)是不超过n且与n互素的正整数的个数。给出正整数n的唯一分解式$n=p_1^{a_1}{p}_2^{a_2}...p_k^{a_k}$，φ函数的公式为：$\phi (n)=n(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k})$。

// 用试除法找出n的所有素因子
int phi(int n){
    int m=sqrt(n+0.5);
    int ans=n;
    for(int i=2;i<=m;i++){
        if(n%i==0){
            ans=ans/i*(i-1);
            while(n%i==0)n/=i;
        }
    }
    if(n>1)ans=ans/n*(n-1);
    return ans;
}

// 用类似埃氏筛法求1~n的phi函数值，复杂度O（nloglogn）。
int phi[Max_n];

void phi_table(int n){
    for(int i=1;i<=n;i++)phi[i]=i;
    for(int i=2;i<=n;i++){
        if(phi[i]==i){ //i是质数
            for(int j=i;j<=n;j+=i)
                phi[j]=phi[j]/i*(i-1); //更新i的倍数
        }
    }
}

8、莫比乌斯函数

描述： 莫比乌斯函数μ(n)定义为

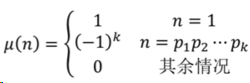
如果n=1，则μ[n]=1；如果n有平方因子，则μ[n]=0；如果n分解后有奇数个不同的素因子，则μ[n]=-1，反之偶数个为1。

莫比乌斯反演： 设$f$是算术函数，$F$是$f$的和函数，$F(n)={\sum }_{d|n}f(d)$，则$f(n)={\sum }_{d|n}\mu (d)F(\frac{n}{d})$，其中$n$是正整数。

9、快速幂

描述： 快速计算底数base的exp次幂，其时间复杂度为 O(log₂N)。

// 快速幂取模
ll quickMod(ll base,ll exp,ll mod){
	base%=mod;
    ll ans=1;
    while(exp){
        if(exp&1)ans=ans*base%mod;
        exp>>=1;
        base=base*base%mod;
    }
    return ans;
}

10、矩阵快速幂

描述： n*n矩阵的exp次幂。

矩阵乘法：$C_{ij}={\sum }_{k=1}^n{a}_{ik}\ast b_{kj}$ 。$C_{ij}$为A的第i行与B的第j列对应乘积的和。

// 矩阵快速幂取模
ll n;  //n*n矩阵
struct Mat{
    ll m[Max_n][Max_n];      // Max_n为二维数组大小n 
	Mat(){memset(m,0,sizeof(m));}
	Mat(ll s[Max_n][Max_n]){ // 使用二维数组s初始化m
		for(int i=0;i<n;i++){
			for(int j=0;j<n;j++)
				m[i][j]=s[i][j];
		}
	}
    Mat operator*(Mat &a){
        Mat b;
        for(int i=0;i<n;i++){
            for(int j=0;j<n;j++)
                for(int k=0;k<n;k++)
                b.m[i][j]=(b.m[i][j]+m[i][k]*a.m[k][j])%mod;
        }
        return b;
    }
};

Mat quickMod(Mat base,ll exp){
    Mat ans;
    for(int i=0;i<n;i++)ans.m[i][i]=1; //单位矩阵初始化
    while(exp){
        if(exp&1)ans=ans*base;
        exp>>=1;
        base=base*base;
    }
    return ans;
}

应用： 主要通过把数放到矩阵的不同位置，然后把普通递推式变成"矩阵的等比数列"，最后快速幂求解递推式。

• 给一些简单的递推式：

  1.f(n)=a*f(n-1)+b*f(n-2)+c；（a,b,c是常数）
  
  2.f(n)=cⁿ-f(n-1) ；（c是常数）
  
  3.f(n)=f(n-1)+(-1)ⁿ*f(n-2)； =>f(n)=f(n-2)+f(n-4)；
  

11、博弈论

1.Bash（巴什博弈）

有一堆石子共有n个。AB两个人轮流拿，A先拿。每次最少拿1颗，最多拿m颗，最后取完者获胜。
取胜策略：拿掉部分物品，使对方面临看k(m+1)的局面。

void solve(int n,int m){
    //n%(m+1)!=0则先手赢，反之后手赢
    printf("%c\n",n%(m+1)?'A':'B');
}

2.Wythoff（威佐夫博弈）

有2堆石子。AB两个人轮流拿，A先拿。每次从一堆中取任意个或从2堆中取相同数量的石子，但不可不取，最后取完者获胜。

性质：我们称Wythoff中的必败态为奇偶局势（a_k,b_k）
①任何自然数都仅包含在一个奇偶局势中；
②a_n+1=前n组必败态中未出现过的最小正整数；
③如果(a_n,b_n)为必败态，则b_n = a_n + n；
结论：a_n=⌊n*(1+√5)/2⌋，bn=a_n+n(n=0,1,2…n)。
故判断（a,b）为奇偶局势，只需要比较(b-a)*(1+√5)/2)==a即可 （其中a<b）。

double g=(sqrt(5)+1)/2;

void solve(int a,int b){
    if(a>b)swap(a,b);
    int t=(b-a)*g;
    if(t==a)printf("B\n"); //必败态(a,b)为奇偶局势
    else printf("A\n");
}

3.Nim（尼姆博奕）

有N堆石子。AB两个人轮流拿，A先拿。每次从一堆中取任意个，但不可不取，最后取完者获胜。
结论：所有堆石子数量异或不为0，则先手胜，反之后手胜。

void solve(){
    int ans=0;
    for(int i=1;i<=n;i++)
        ans^=s[i];
    //ans不为0则先手赢，否则后手赢
    printf("%c\n",ans?'A':'B');
}

4.组合游戏
SG函数：对于任意状态x，定义SG(x)=mex{S}，S是x的后继状态的SG函数值集合，mex(S)表示不在S内的最小非负整数。
SG定理：把原游戏（组合游戏）分解成多个独立的子游戏，则原游戏的SG函数值是它的所有子游戏的SG函数值异或。
即：sg(G)=sg(G1)^ sg(G2) ^ …^ sg(Gn)。

SG值计算方法：
1.可选步数为1~m的连续整数，直接取模即可，SG(x)=x%(m+1)；
2.可选步数为任意步，SG(x) = x；
3.可选步数为一系列不连续的数，用SG函数求解；

#打表求SG函数值#

//f[N]:可改变当前状态的方式，共N种（从小到大排）
//sg[]:0~n的SG函数值
//s[]:为x后继状态的SG函数值集合
int f[Max_n],sg[Max_n];
bool s[Max_n];

void getSG(int n){
    memset(sg,0,sizeof(sg));
    for(int i=1;i<=n;i++){
        memset(s,0,sizeof(s));
        for(int j=0;f[j]<=i&&j<N;j++)
            s[sg[i-f[j]]]=1;
        for(int j=0;j<=i;j++){ //求mex(S)中未出现的最小非负整数
            if(!s[j]){sg[i]=j;break;}
        }
    }
}

#递归求SG函数值#

//f[N]:可改变当前状态的方式，共N种（从小到大排）
//sg[]:0~n的SG函数值
int f[Max_n],sg[Max_n];

int dfs_SG(int x){
    if(sg[x]!=-1)return sg[x];
    bool s[Max_n];    //s[]:为x后继状态的SG函数值集合
    memset(s,0,sizeof(s));
    for(int i=0;f[i]<=x&&i<N;i++){
        dfs_SG(x-f[i]);
        s[sg[x-f[i]]]=1;
    }
    for(int i=0;i<=x;i++){
        if(!s[i]){sg[x]=i;break;}
    }
    return sg[x];
}

12、生成排列

字典序法： 按照字典排序的思想逐一生成所有排列。设当前的排列为$p=p_1...p_{i-1}{p}_i...p_n$，实现原理为C++标准库中的next_permutation函数（pre_permutation函数类似原理实现）：

1. 从右向左找到第一个增序对的尾元素，下标$i$： i = m a x { k ∣ p k − 1 &lt; p k } i=max\{k|p_{k-1}&lt;p_k\} i=max{k∣pk−1​<pk​}
2. 在$p_{i-1}$元素后面找比$p_{i-1}$大的最后一个元素，下标$j$： j = m a x { k ∣ p k &gt; p i − 1 } j=max\{k|p_k&gt;p_{i-1}\} j=max{k∣pk​>pi−1​}
3. 互换$p_{i-1}$与$p_j$，得到序列：$p=p_1...p_{i-2}$$p_j$$p_i...p_{j-1}{p}_{i-1}{p}_{j+1}...p_n$
4. 反排$p_j$后面的元素，使其递增，得到序列：$p=p_1...p_{i-2}{p}_j{p}_n...p_{j+1}{p}_{i-1}{p}_{j-1}...p_i$

bool next(int n){ // 生成下一个排列
    int i,j;
    for(i=n-1;i>=1;i--){
        if(s[i-1]<s[i]){
            for(j=n-1;j>=i;j--){
                if(s[j]>s[i-1]){
                    swap(s[i-1],s[j]);
                    reverse(s+i,s+n);
                    break;
                }
            }
            break;
        }
    }
    if(i!=0)return true;
    return false;
}

13、排列组合计数

排列问题: $P(n,r)$表示从$n$个不同元素中取$r$个元素，并按次序排列的排列个数。$P(n,r)=\frac{n!}{(n-r)!}$。
组合问题: $C(n,r)$表示从$n$个不同元素中取$r$个元素，不考虑次序的组合个数$。C(n,r)=\frac{n!}{r!\ast (n-r)!}$。
常用性质:

1. $C(n,0)=C(n,n)=1$
2. $C(n,k)=C(n,n-k)$
3. $C(n+1,k+1)=C(n,k)+C(n,k+1)$
4. $C(n,k+1)=C(n,k)\ast (n-k)/(k+1)$

有重复元素的全排列： 有$k$个元素，其中第$i$个元素有$n_i$个，全排列个数为：$\frac{n!}{n_1!\ast n_2!...n_k!}$。
可重复选择的组合： 有$n$个不同的元素，每个元素可以选择多次，一共选$k$个元素，组合个数为：$C(n+k-1,k)$。

// 运用性质3预处理[n,m]以内的组合数
void solve(ll n,ll m){
     for(int i=0;i<=m;i++)
        c[i][0]=1;
     for(int i=1;i<=n;i++){
        for(int j=1;j<=i;j++)
            c[i][j]=c[i-1][j]+c[i-1][j-1];
     }
}

// 运用性质4递推计算组合数C(n,k)
ll solve(ll n,ll k){
    if(k>n-k)k=n-k;
    ll ans=1;
    for(int i=1;i<=k;i++){
        ans*=(n+1-i);
        ans/=i;
    }
    return ans;
}

Catalan数:

卡特兰数是$C_n={\sum }_{i=0}^{n-1}{C}_i{C}_{n-1-i}=C_0{C}_{n-1}+C_1{C}_{n-2}+...+C_{n-1}{C}_0$的序列，其中$C_0=1$。

公式： $C_n=\frac{C(2n,n)}{n+1},n\ge 0$ 或 $C_n=\frac{4n-2}{n+1}\ast C_{n-1},n>0$

序列：1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786（下标从0开始）

Bell数:

贝尔数$B_n$是包含$n$个元素集合的划分方法的数目。$B_{n+1}={\sum }_{k=0}^{n}C(n,k)B_k$（$B_0=1$）。

序列：1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975（下标从0开始）

构造Bell三角形：

1. 第一行第一项是1。（a[0][0]=1）
2. 对于n>1，第n行第一项等同于第n-1行的最后一项。（a[n,1]=a[n-1][n-1]）
3. 对于m,n>1，第n行第m项等于它左边和左上方的两个数之和。（a[n][m]=a[n][m-1]+a[n-1][m-1]）
   
   每行首项是Bell数。

Stirling数:

1. 第一类Stirling数：表示将$n$个不同元素放入$k$个环排列的方式的数目。$s(n,k)=s(n-1,k-1)+(n-1)\ast s(n-1,k)$，其中$s(n,0)=s(1,1)=1$。
2. 第二类Stirling数：表示将$n$个不同元素的集合划分为$k$个不为空的子集的方式的数目。$S(n,k)=S(n-1,k-1)+k\ast S(n-1,k)$，其中$S(n,n)=S(n,1)=1$。
   显然，每个贝尔数都是第二类斯特林数的和，$B_n={\sum }_{k=1}^{n}S(n,k)$。

错排数:

错排数是对于一个排列，每个元素都不在自己原来位置的排列数。$D_1=0;D_2=1;D_n=(n-1)(D_{n-2}+D_{n-1})$ ，其中$n>2$。

序列：0,1,2,9,44,265,1854,14833,133496（下标从1开始）

14、鸽笼原理和容斥原理

鸽笼原理: 解决存在性问题的常用方法，运用是要分析清楚什么是鸽子（元素），什么是笼（集合）。鸽笼原理的三种形式表述：

1. 将n+1个元素放入n个集合内，则至少有一个集合有不少于两个元素。
2. 把m个元素任意放入n个集合里（n<m），则至少有一个集合有不少于$\lceil \frac{m}{n}\rceil$个元素。
3. 把无穷多个元素放入有限个集合内，则至少有一个集合有无穷多个元素。

应用：任意给出$m$个整数$a_1,a_2,a_3,...,a_m$。
证明：必存在整数 $s,t(0\le s＜t\le m)$,使得 $m$ 整除 $a_{s+1}+a_{s+2}+\dots +a_t$。

证：令 $S_1=a_1,S_2=a_1+a_2,\dots ,S_m=a_1+a_2+\dots +a_m$，若 $m$ 整除 $S_k$，问题得证；否则根据鸽笼原理（笼为余数），余数只能在 $1,2,\dots ,m-1$中间选择，一定存在 $S_s,S_t$余数相同，根据相关数论定理：$S_t-S_s=a_{s+1}+\dots +a_t$能被 $m$整除。

容斥原理: 应用于计算有限集的并集中的元素个数。|A∪B∪C| = |A|+|B|+|C| - |A∩B| - |B∩C| - |C∩A| + |A∩B∩C|（奇数为正，偶数为负）。

15、生成函数

幂级型生成函数:
设$a_0,a_1,a_2,...a_n...$是一个数列，构造形式幂级数$f(x)=a_0+a_{1}x+a_2{x}^2+...+a_n{x}^n+...$，称$f(x)$是数列$a_0,a_1,a_2,...a_n...$的幂级型生成函数。幂级型生成函数可用来求解多重集的组合计数问题。

【出处】
表达式：解题时首先要写出表达式，通常是多项的乘积，每项由多个$x^y$组成。如：$(1+x+x^2)$$(1+x^4+x^8)(x^5+x^{10}+x^{15})$。
通用表达式：$(x^{v[i]\ast n1[i]}+x^{v[i]\ast (n1[i]+1)}+x^{v[i]\ast (n1[i]+2)}+...+x^{v[i]\ast n2[i]})$，表示第$i$个表达式（1<=i<=K）。
K：对应具体问题中物品的种类数。
v[i]：表示该乘积表达式第i个因子的权重，对应于具体问题的每个物品的价值或者权重。
n1[i]：表示该乘积表达式第i个因子的起始系数，对应于具体问题中的每个物品的最少个数，即最少要取多少个。
n2[i]：表示该乘积表达式第i个因子的终止系数，对应于具体问题中的每个物品的最多个数，即最多要取多少个。
对于表达式$(1+x+x^2)(x^8+x^{10})(x^5+x^{10}+x^{15}+x^{20})$，v[3]={1,2,5}，n1[3]={0,4,1}，n2[3]={2,5,4}。
解题的关键是要确定v、n1、n2数组的值。 通常n1都为0，但有时候不是这样。n2有时候是无限大。根据v、n1、n2、P的要求简单修改模板即可。

通用模板：

int K,P;  //K为种类数，P为最大可能的指数
int n1[Max_n],n2[Max_n],v[Max_n];
int a[Max_n],b[Max_n]; //a为计算结果，b为中间结果。

void solve(){
    memset(a,0,sizeof(a));
    a[0]=1;
    for(int i=1;i<=K;i++){ //循环每个因子
        memset(b,0,sizeof(b));
        for(int j=n1[i];j<=n2[i]&&j*v[i]<=P;j++)//循环每个因子的每一项
            for(int k=0;k+j*v[i]<=P;k++)        //循环a的每个项
                b[k+j*v[i]]+=a[k];  //把结果加到对应位
        memcpy(a,b,sizeof(b));      //b赋值给a
    }
}

优化模板： 用一个last变量记录目前最大的指数，这样只需要在0…last上进行计算。

int K,P;  //K为种类数，P为最大可能的指数
int n1[Max_n],n2[Max_n],v[Max_n];
int a[Max_n],b[Max_n]; //a为计算结果，b为中间结果。

void solve(){
    memset(a,0,sizeof(a));
    a[0]=1;
    int last=0,last2;
    for(int i=1;i<=K;i++){
        last2=min(last+n2[i]*v[i],P);      //计算下一次的last
        memset(b,0,sizeof(int)*(last2+1)); //只清空b[0,last2]
        for(int j=n1[i];j<=n2[i]&&j*v[i]<=last2;j++)   //这里是last2
            for (int k=0;k<=last&&k+j*v[i]<=last2;k++) //这里前者last，后者last2
                b[k+j*v[i]]+=a[k];
        memcpy(a,b,sizeof(int)*(last2+1)); //b赋值给a，只赋值b[0,last2]
        last=last2;   //更新last
    }
}

指数型生成函数:
设$a_0,a_1,a_2,...a_n...$是一个数列，构造形式幂级数$f(x)={\sum }_{r=0}^{\infty }\frac{a_r}{r!}{x}^r=a_0+a_{1}x+\frac{a_2}{2!}{x}^2+...+\frac{a_n}{n!}{x}^n+...$，称$f(x)$是数列$a_0,a_1,a_2,...a_n...$的指数型生成函数。指数型生成函数可用来求解多重集的排列计数问题。

66666666666666666666666666