红黑树基础-第一篇

一、红黑树的定义和性质

红黑树是一种含有红黑结点并能自平衡的二叉查找树。它并且满足下面定义：

定义1. 每个节点要么是黑色，要么是红色。

定义2. 根节点是黑色。

定义3. 每个叶子节点(Nil)是黑色。

定义4. 每个红色结点的两个子结点一定都是黑色。

定义5. 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

注意：为了统一名称，便于理解。本文所称结点均为非空，即不是Nil，空节点我们统称为叶子结点，也就是Nil。另外结点同节点，虽然两者不一样，但是本文暂不做区分。

根据红黑树以上五条定义，我们可以推导出以下几点性质和可能情景：

性质1. 父子节点不可能同时是红节点，即红节点不连续。否则违反定义4

性质2. 如果某节点的一个子节点是黑色，那么该节点必然存在另一个子节点。否则违反定义5

情景1. 一个结点的两个子节点出现一个是红色，一个是黑色的情况是可能出现的

情景2. 父子节点同时是黑色的情况是可能出现的

规律1. 新插入的节点初始化为红色，能最小化变色操作

下面我们来看一下一个典型的红黑树结构，如下图：

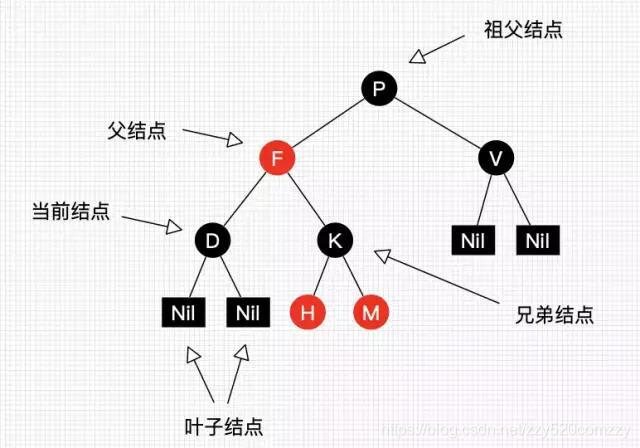
                                                                              图1：一个简单的红黑树

上图就是一颗简单的红黑树。其中 Nil 为叶子结点，并且它是黑色的。(值得提醒注意的是，在 Java 中，叶子结点是为 null 的结点。)
红黑树并不是一个完美平衡二叉查找树，从图 1 可以看到，根结点 P 的左子树显然比右子树高。
但左子树和右子树的黑结点的层数是相等的，也即任意一个结点到到每个叶子结点的路径都包含数量相同的黑结点(性质 5)。

前面讲到红黑树能自平衡，它靠的是什么?有如下三种操作：

左旋：以某个结点（例如p）作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，左子结点保持不变。如图 2。

右旋：以某个结点（例如p）作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。如图 3。

变色：结点的颜色由红变黑或由黑变红。

                                                                                          图2：左旋

                                                                                          图3：右旋

我们先忽略颜色，可以看到旋转操作不会影响旋转结点的父结点，父结点以上的结构还是保持不变的。
左旋只影响旋转结点和其右子树的结构，把右子树的结点往左子树挪了;右旋只影响旋转结点和其左子树的结构，把左子树的结点往右子树挪了。
但要保持红黑树的性质，结点不能乱挪，还得靠变色了。怎么变?那就要红黑树通过旋转和变色达到自平衡。

红黑树的查找

因为红黑树是二叉查找树，查找一个节点是典型的二分查找，log(n)的复杂度，这里就不再说明了

红黑树的插入

假设插入位置已经通过二分查找找到，把插入结点放到叶子结点就可以啦，但插入结点应该是什么颜色呢?
答案是红色。理由很简单，红色在父结点(如果存在)为黑色结点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。
但如果插入结点是黑色，那么插入位置所在的子树黑色结点总是多 1，必须做自平衡。

所有插入情景如图 4 所示：

                                                                                   图4：红黑树平衡插入场景

嗯，插入情景很多呢，8 种插入情景!但情景 1、2 和 3 的处理很简单，而情景 4.2 和情景 4.3 只是方向反转而已。

懂得了一种情景就能推出另外一种情景，所以总体来看，并不复杂，后续我们将一个一个情景来看，把它彻底搞懂。

另外，根据二叉树的性质，除了情景 2，所有插入操作都是在叶子结点进行的。这点应该不难理解，因为查找插入位置时，我们就是在找子结点为空的父结点的。

在开始每个情景的讲解前，我们还是先来约定下，如图 5 所示：

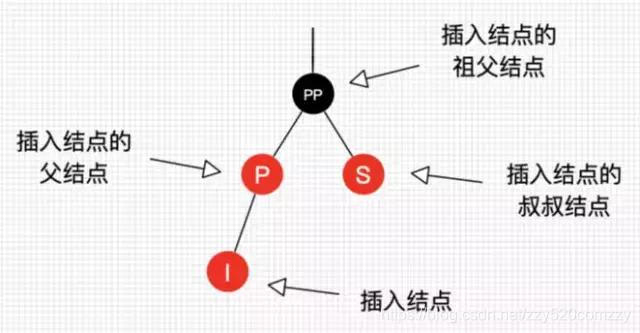
                                                                                   图5：插入操作结点的叫法约定

图 5 的字母并不代表结点 Key 的大小。I 表示插入结点，P 表示插入结点的父结点，S 表示插入结点的叔叔结点，PP 表示插入结点的祖父结点。

好了，下面让我们一个一个来分析每个插入的情景以及处理。

情景 1：红黑树为空树

最简单的一种情景，直接把插入结点作为根结点就行，但注意，根据红黑树性质 2：根节点是黑色。还需要把插入结点设为黑色。

处理：把插入结点作为根结点，并把结点设置为黑色。

情景 2：插入结点的 Key 已存在

插入结点的 Key 已存在，既然红黑树总保持平衡，在插入前红黑树已经是平衡的，那么把插入结点设置为将要替代结点的颜色，再把结点的值更新就完成插入。

处理：把 I 设为当前结点的颜色，更新当前结点的值为插入结点的值。

情景 3：插入结点的父结点为黑结点

由于插入的结点是红色的，当插入结点是黑色时，并不会影响红黑树的平衡，直接插入即可，无需做自平衡。

处理：直接插入。

情景 4：插入结点的父结点为红结点

再次回想下红黑树的定义 2：根结点是黑色。如果插入的父结点为红结点，那么该父结点不可能为根结点，所以插入结点总是存在祖父结点。这点很重要，因为后续的旋转操作肯定需要祖父结点的参与。

情景 4 又分为很多子情景，下面将进入重点部分，各位看官请留神了。

情景 4.1：叔叔结点存在并且为红结点。

从红黑树定义4 可以看出，祖父结点肯定为黑结点，因为不可以同时存在两个相连的红结点。

那么此时该插入子树的红黑层数的情况是：黑红红。显然最简单的处理方式是把其改为：红黑红。如图 6 和图 7所示。

处理：将 P 和 S 设置为黑色，将 PP 设置为红色，把 PP 设置为当前插入结点。

                                                                                   图6：插入情景 4.1_1

                                                                                   图7：插入情景 4.1_2

图6和图7只是两种例子，实际有四种，就不一一列举了，效果一样。

可以看到，我们把 PP 结点设为红色了，如果 PP 的父结点是黑色，那么无需再做任何处理。

但如果 PP 的父结点是红色，根据定义 4，此时红黑树已不平衡了，所以还需要把 PP 当作新的插入结点，继续做插入操作自平衡处理，直到平衡为止。

试想下 PP 刚好为根结点时，那么根据定义 2，我们必须把 PP 重新设为黑色，那么树的红黑结构变为：黑黑红。

换句话说，从根结点到叶子结点的路径中，黑色结点增加了。这也是唯一一种会增加红黑树黑色结点层数的插入情景。

我们还可以总结出另外一个经验：红黑树的生长是自底向上的。这点不同于普通的二叉查找树，普通的二叉查找树的生长是自顶向下的。

情景 4.2：叔叔结点不存在或为黑结点，并且插入结点的父亲结点是祖父结点的左子结点。

单纯从插入前来看，也即不算情景 4.1 自底向上处理时的情况，也就是初次插入节点，不是向上回溯插入情况，叔叔结点非红即为叶子结点(Nil)。

因为如果叔叔结点为黑结点，而父结点为红结点，那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了，这不满足红黑树的定义 5。后续情景同样如此，不再多做说明了。

前文说了，需要旋转操作时，肯定一边子树的结点多了或少了，需要租或借给另一边。插入显然是多的情况，那么把多的结点租给另一边子树就可以了。

情景 4.2.1：插入结点是其父结点的左子结点。

处理：将 P 设为黑色，将 PP 设为红色，对 PP 进行右旋。

                                                                                   图8：插入情景 4.2.1

现在我们来分析一下这个右旋，由图 8 可得，右旋前PP节点是黑色，旋转后，P节点也是黑色，旋转过程使PP的父节点变成了P的父节点，而旋转前后该节点的颜色都是黑色，也就是说旋转不会影响旋转前PP父节点及以上的树结构，再来看右旋会使P的右子树变成旋转后PP的左子树（对右旋不清楚的同学请仔细看右旋对结构的影响），可以看到旋转前P为红色，旋转后PP也为红色，也就是说，旋转对旋转前P的子树也没有影响。综上可得，该情形一次性4.2.1的操作处理即可达到自平衡。

情景 4.2.2：插入结点是其父结点的右子结点。

这种情景显然可以转换为情景 4.2.1，如图 9 所示。

处理：对 P 进行左旋，把 P 设置为插入结点，得到情景 4.2.1，进行情景 4.2.1 的处理。

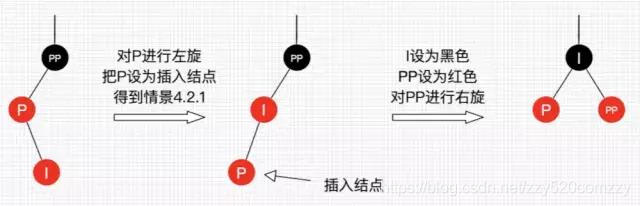
                                                                                   图9：插入情景 4.2.2

情景 4.3：叔叔结点不存在或为黑结点，并且插入结点的父亲结点是祖父结点的右子结点。

该情景对应情景 4.2，只是方向反转，不做过多说明了，直接看图。

情景 4.3.1：插入结点是其父结点的右子结点。

处理：将 P 设为黑色，将 PP 设为红色，对 PP 进行左旋。

                                                                                   图10：插入情景 4.3.1

情景 4.3.2：插入结点是其父结点的右子结点。

处理：对 P 进行右旋，把 P 设置为插入结点，得到情景 4.3.1，进行情景 4.3.1 的处理。

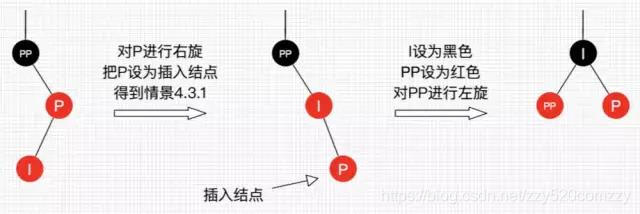
                                                                                   图11：插入情景 4.3.2

好了，讲完插入的所有情景了。可能有同学会想：上面的情景举例的都是第一次插入而不包含自底向上处理的情况，那么上面所说的情景都适合自底向上的情况吗?答案是肯定的。

理由很简单，只要每棵子树都能自平衡，那么整棵树最终总是平衡的。

另外，当叔叔节点为Nil时很好理解，当叔叔节点是黑节点时你们能理解吗？其实这种情况发生在自底向上的插入处理中，而且Nil也是黑色，在旋转过程中也是满足红黑自平衡特性的，同学们不妨仔细琢磨一下，记得一定要画图。

平衡插入的原理就讲完了，还剩红黑树的平衡删除，放到红黑树基础-第二篇