
💡 本次解读的文章是2020年发表于 Springer 的一篇与智能合约 Gas 优化相关的论文, 在这篇文章中,作者提出了一种新的基于 Max-SMT 的智能合约超优化方法,该方法分为两个步骤:
(1)从智能合约的基本块中提取堆栈功能规范(Stack functional specification,SFS);
(2)基于 SFS 抽象,通过 Max-SMT 编码,合成具备最少 gas 消耗的优化块字节码。
1、背景介绍
在区块链生态系统中,由于每天交易的数量较为庞大,且每笔交易需要消耗一定的交易费用(gas),因此,以节能的方式优化程序显得尤为重要。虽然,Solidity文档和一些相关文档给出了 gas 消耗的模式,提出用 gas-efficient 模式的替换,且 Solidity 的编译器也尝试优化字节码以最小化其 gas 消耗(如 solc 编译器的优化标志优化了大常数的存储和调度程序,以此减少 gas 的消耗),但是即便如此,编译后的 EVM 代码并不总是如期望的那样高效。
另外,在 Gas 优化的研究方面,超优化是30多年前提出的一种技术,它试图通过穷举搜索(exhaustive search)找到一个代码块的最佳翻译,以尝试产生相同结果的所有可能的指令序列,虽然这种方式简单,但是在计算量上的要求极高。文献 [ 1 ] [1] [1] 提出了“无界”超优化(“unbounded” super-optimization)的思想,即将对目标程序的搜索转移到求解器(solver)。而最近,这种“无界”超优化被应用于以太坊字节码基本块(basic block)的优化 [ 2 ] [2] [2],结果表明这一方法存在着极端的计算要求,而这种实施过程中的复杂性主要体现在三个方面:
- 该问题用位向量算术理论(the theory of bit-vector arithmetic)表示,位宽大小为256,这对于大多数 SMT 求解器来说是一个具有挑战性的宽度尺寸;
- 在表达问题过程中需要涉及到存在全量化(exists-forall quantification),因为希望找到一个对初始堆栈中所有值都有效的指令分配;
- 由于解决思路是寻找 gas 最优字节码,所以这个问题不是一个满意度问题,而是一个最优化问题。
2、本文贡献
本文的贡献在于提出了一种基于 Max-SMT 合成优化 EVM 模块的智能合约 gas 优化方法,与其他工作的区别在于:
- Stack functional specification(SFS,栈功能规范),本文的方法将 EVM 字节码作为输入,并基于通过符号执行获得字节码的 control-flow graph(CFG,控制流程图)来获取每一代码块的输入和输出 SFS。SFS 确定了块需要计算的目标栈,并使用一组规则进行简化,这些规则捕获了与 gas 优化相关的算术、位、关系等EVM操作的大部分语义。
- Synthesis problem using SMT,本文将优化作为一个合成问题(synthesis problem)来处理,其中 SMT 求解器用于合成最优的 EVM 字节码,对于功能规范中给定的输入堆栈,生成由规范确定的目标堆栈。本文提出了一个非常有效的编码,与以前的尝试不同,在一个非常简单的整数算术片段中只使用存在量化(existential quantification),只有栈操作( PUSH、DUP、SWAP等)的语义被编码,而所有其他操作都被视为无解释的函数(uninterpreted functions)。
- Use of Max-SMT,通过添加编码所选指令的 gas 成本的软约束来使用 Max-SMT 对优化问题进行编码,添加所需的权重,利用 Max-SMT 优化器改进搜索过程。
- Experiments,在 ( i ) 用于评估工具 ebso 且来自 [ 2 ] [2] [2]的相同数据集和 ( ii ) 以太坊区块链上最有名的128个合约进行评估。实验结果表明:与 ebso 在( i )中 92.12 % 的块中超时相比,本文的方法只在 8.64 % 的块中超时,并且获得了比 ebso 大两个数量级的增益;对于集合( ii ),本文的方法获得了占总 gas 的 0.59 %的节省。
虽然超优化的目的是在基本块(块内,intra-block)的水平上进行优化,但本文从给定的 SFS 中合成 EVM 码的方法也可以应用在更丰富的优化框架中,从而实现多个基本块(块间,inter-block)的优化。
3、合成过程介绍
在介绍本文的具体方法实现前,作者首先对从给定的 EVM 字节码合成超优化智能合约的方法进行了总体概述。在这部分中,本文以一段 Solidity 代码(左侧)和由 solc 编译器优化而成的 EVM 字节码(右侧)作为例子(Example),对合成优化代码的过程进行了描述。

3.1 字节码介绍
在了解合成流程之间,需要对本文涉及到的字节码有一定的认识。在字节码部分,本文依据字节码的含义对字节码进行了分类,并说明了字节码具体消耗的 gas 值,这些是为后续论文的优化过程做铺垫。
字节码分类
在字节码方面,本文主要分成了两大类,一类是仅仅指 DUP、PUSH、SWAP 和 POP 这些仅修改堆栈而不执行计算的堆栈操作码 stack operations,另一类是除 stack operations 的 other operations。
- stack operations:
(1)PUSHX: 字节码将值 A 存储在栈顶
(2)DUPX: 将存储在位置 X - 1 的元素复制到栈顶
(3)SWAPX: 将存储在栈顶的值与存储在位置 X 的值交换
(4)POP: 删除存储在栈顶的值(使用列表操作remove删除给定位置的元素)
- other operations:
(1)SLOAD、SSTORE: 访问存储在合约存储中的持久数据
(2)MLOAD、MSTORE: 访问存储在本地内存中的数据
(3)JUMP、JUMPI: 跳转到不同代码地址位置
(4)CALL、DELEGATECALL、CALLCODE、CALLSTATIC: 调用不同合约上的函数
(5)LOG: 写日志
(6)GAS、CALLER、BLOCKHASH: 访问关于区块链和交易的信息
(7)CODECOPY、RETURNDATACOPY: 复制与外部调用
(8)OP: 表示与栈操作相关的所有其他EVM字节码(算术和位运算等)
考虑到本文的方法是基于优化修改堆栈操作的,因此没有对那些在堆栈中没有体现效果的字节码进行优化,例如 MSTORE、SSTORE、LOG 或 EXTCODECOPY 等。另外,排除了 JUMPDEST 和 JUMP 这两个无法优化的操作码(即不参与 gas 消耗的计算)。
字节码 Gas 消耗
基于如文献3所述,来自so-called base family(如 POP)的操作消耗 2,来自verylow family(如PUSH、SWAP、ADD等)的操作消耗 3,来自low family(如MUL、DIV等)的操作消耗 5等等,计算得到实例对应的 gas 消耗为76。
3.2 合成流程介绍
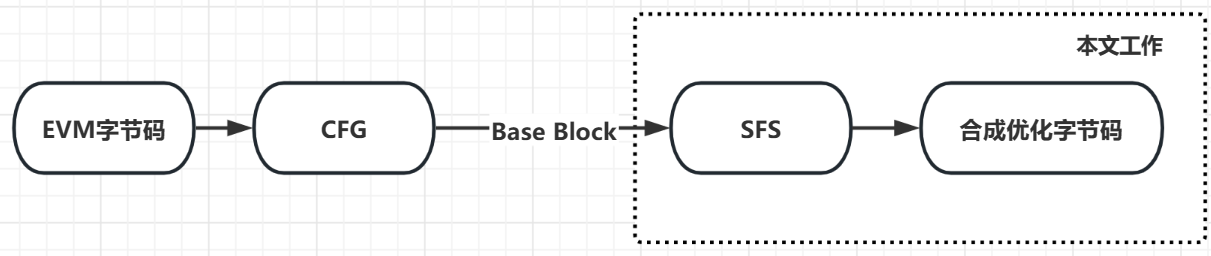
在智能合约 gas 优化方面的思路是首先从 EVM 字节码中获取控制流图 CFG,接着利用 CFG 获取基本代码块,在代码块的基础上,提取 SFS 并以此作为优化算法的输入,合成 gas 消耗最小的字节码。其中,本文的工作主要是将构成字节码控制流图(CFG)的块集合作为输入,提取 SFS 并合成 gas 消耗最小的字节码,最终输出合成的优化字节码。
- SFS 的提取
在提取的过程中,以 CFG 获取的代码块对象作为输入,提取用于对进入块时的初始堆栈和执行块后的最终堆栈的功能描述 SFS。其中,SFS 主要通过对初始堆栈元素的符号一阶项来定义,Example 对应的 SFS 如图所示,图中左侧表示初始栈,右侧表示最终栈。初始栈包含五个元素 x 0 , … , x 4 x_{0},\ldots, x_{4} x0,…,x4,最终栈包含两个元素:顶部为 x 4 x_{4} x4,底部为符号项 e x p ( x 2 + x 3 , x 0 + x 1 ) exp(x_{2} + x_{3}, x_{0} + x_{1}) exp(x2+x3,x0+x1)。

- 字节码的合成
本文利用两个例子说明了合成过程中不同选择所带来的 gas 消耗的不同,并展示了合成最优字节码的过程,这两个例子说明即使有指导搜索的函数规范,如果想确保找到最优的字节码,也必须穷尽所有可能的方法来获得它。
(1)Example 1
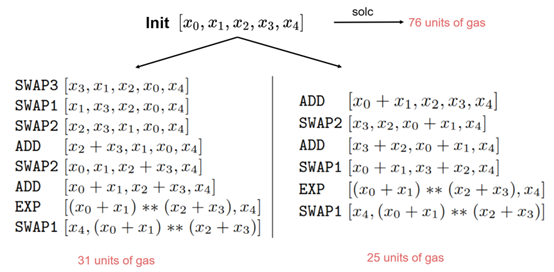
(2)Example 2
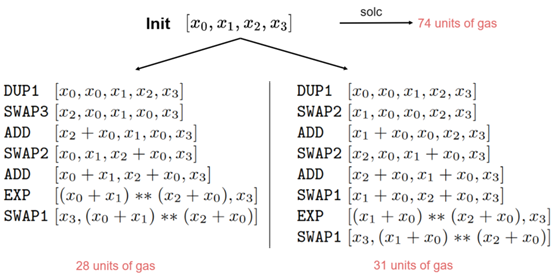
然而,与其他超优化方法不同,本文在处理所有的 non-stack operations 上进行了限制,如将ADD、SUB、AND、OR、LT 等作为未解释字节码(uninterpreted bytecodes),以此简化编码的过程:
- 通过将它们视为无解释的字节码,可以避免使用宽度为256的位向量理论进行推理;
- 可以在存在量化(existentially quantified)片段中表达问题,避免存在/整体(exists/forall)的交替:
(1)从 SFS 开始,通过引入新变量(fresh variables)来抽象出用无解释的函数构建的所有项,这样每一个新变量代表一个项 f ( a 1 , … , a n ) f(a_{1}, \ldots , a_{n}) f(a1,…,an),其中每一个 a i a_{i} ai 是一个(256 bit)数值,或者是一个新变量(fresh variables),或者是一个初始堆栈变量(initial stack variable)。另外,还通过对每个项都有一个单一变量来共享,由此将无解释的字节码用数值进行简单表示。
(2)为了避免全称量化,可以规定 PUSH 操作码在堆栈中只能引入0到 2 256 − 1 2^{256} - 1 2256−1的值,因此,可以从 2 256 2^{256} 2256 开始给新变量(fresh variables)和初始堆栈变量(initial stack variable)赋值,以此避免它们与问题中其他值之间的混淆。
另外,本文对合成过程涉及的数值量进行了符号表示:
(1)一个解所允许的操作码的最大数目
n
n
n 和栈的最大大小
h
h
h
(2)
O
0
,
…
,
O
n
−
1
O_{0}, \ldots, O_{n-1}
O0,…,On−1 表示字节码操作
(3)
p
0
,
…
,
p
n
−
1
p_{0}, \ldots, p_{n-1}
p0,…,pn−1 表示当
O
i
O_{i}
Oi 是 PUSH 时,添加入栈的值
p
i
p_{i}
pi (
0
≤
p
i
≤
2
256
−
1
0\le p_{i} \le 2^{256}-1
0≤pi≤2256−1)
(4)
s
0
i
,
…
,
s
h
−
1
i
s_{0}^{i}, \ldots, s_{h-1}^{i}
s0i,…,sh−1i 表示执行操作
O
i
O_{i}
Oi 前栈的内容,其中
s
0
i
s_{0}^{i}
s0i 表示栈顶元素
对于无解释的字节码 f u f_{u} fu,有: y = f u ( a 1 , … , a m ) y = f_{u}(a_{1}, \ldots, a_{m}) y=fu(a1,…,am) ,其中 a 1 , … , a m a_{1}, \ldots, a_{m} a1,…,am 是第 i i i 步中栈顶元素 s 0 i , … , s m − 1 i s_{0}^{i}, \ldots, s_{m-1}^{i} s0i,…,sm−1i,经过操作后可以得到第 i + 1 i+1 i+1 步骤执行前的栈顶元素 y , s m i , … y, s_{m}^{i}, \ldots y,smi,…。另外,本文还对 ADD、MUL、AND、OR等无解释字节码的交换性进行了编码,这主要通过考虑两个在堆栈顶部的参数发生的可能顺序,其他属性如联结性更难编码,留待未来发展。
进一步地,在 SMT 的基础上,本文采用了 Max-SMT进行最优合成。SMT 问题的每个解都将具有与给定解相同的 SFS,因此,只需要寻找 gas 成本最小的解。在 [ 2 ] [2] [2]中,这是通过在 SMT求解过程的顶端实现一个循环来实现的,该循环调用求解器,每次请求一个 gas 方面更好的解,这也是在 SMT 问题中编码的。这样的方法不能很容易地以增量的方式实现,将 SMT 求解器作为一个黑盒而没有相应的性能惩罚。因此,本文提出将问题编码为一个 Max-SMT 问题,这样可以很容易地使用任何 Max-SMT 优化器,如Z3、Barcelogic或( Opti ) MathSAT,作为一个具有重要效率增益的黑盒。另外,Max-SMT 编码在之前定义的 SMT 编码中增加了一些软约束,表明了选择每个家族操作符的代价。
4、合成过程实现
如前文所述,最优代码的合成过程包括:1)控制流图获取;2)栈功能规范提取;3)最优字节码合成。其中,控制流图的获取不是本文的关注重点,目前的获取工具有EthIR, Madmax, Mythril 以及 Rattle等等。
4.1 栈功能规范提取
(1)block-partitioning,块划分
通过 CFG 的获取,可以得到 Base Block(基本块,即不包含任何 JUMP 字节码的EVM指令序列),这种基本块由于存在未优化的字节码指令,因此,需要执行进一步的块划分,将基本块划分成多个子块。对于给定的基本块 B = [ b 0 , b 1 , … , b n ] B=\left[b_{0}, b_{1}, \ldots, b_{n}\right] B=[b0,b1,…,bn] ,块划分定义为:
blocks ( B ) = { B i ≡ b i , … , b j ( ∀ k . i < k < j , b k ∉ Jump ∪ Terminal ∪ Split ∪ { JUMPDEST } ) ∧ ( i = 0 ∨ b i − 1 ∈ Split ∪ { JUMPDEST } ) ∧ ( j = n ∨ b j + 1 ∈ Jump ∪ Split ∪ Terminal ) } \operatorname{blocks}(B)=\left\{\begin{array}{l|l} B_{i} \equiv b_{i}, \ldots, b_{j} & \left.\begin{array}{l} \left(\forall k . i<k<j, b_{k} \notin \text { Jump } \cup \text { Terminal } \cup \text { Split } \cup\right. \\ \{\text { JUMPDEST }\}) \wedge\left(i=0 \vee b_{i-1} \in \text { Split } \cup\{\text { JUMPDEST }\}\right)\wedge \\ \left(j=n \vee b_{j+1} \in \text { Jump } \cup \text { Split } \cup \text { Terminal }\right) \end{array}\right. \end{array}\right\} blocks(B)=⎩ ⎨ ⎧Bi≡bi,…,bj(∀k.i<k<j,bk∈/ Jump ∪ Terminal ∪ Split ∪{ JUMPDEST })∧(i=0∨bi−1∈ Split ∪{ JUMPDEST })∧(j=n∨bj+1∈ Jump ∪ Split ∪ Terminal )⎭ ⎬ ⎫
其中:
Jump = { JUMP, JUMPI } Terminal = { RETURN, REVERT, STOP, INVALID } Split = { SSTORE, MSTORE, LOGX, CALLDATACOPY, CODECOPY, EXTCODECOPY, RETURNDATACOPY } \begin{aligned} \text { Jump }= & \{\text { JUMP, JUMPI }\} \\ \text { Terminal }= & \{\text { RETURN, REVERT, STOP, INVALID }\} \\ \text { Split }= & \{\text { SSTORE, MSTORE, LOGX, CALLDATACOPY, CODECOPY, EXTCODECOPY, } \\ & \text { RETURNDATACOPY }\} \end{aligned} Jump = Terminal = Split ={ JUMP, JUMPI }{ RETURN, REVERT, STOP, INVALID }{ SSTORE, MSTORE, LOGX, CALLDATACOPY, CODECOPY, EXTCODECOPY, RETURNDATACOPY }
如前文所述,那些在堆栈上没有体现其作用的字节码将会导致分割,并在碎片化的子块中被省略。论文给出了一个具体的实例来说明块的划分。从图中可以看到,原始的 CFG 块包含字节码 SSTORE、MSTORE 和LOG2,因此,它被分割成三个不包含这些字节码的不同子块。
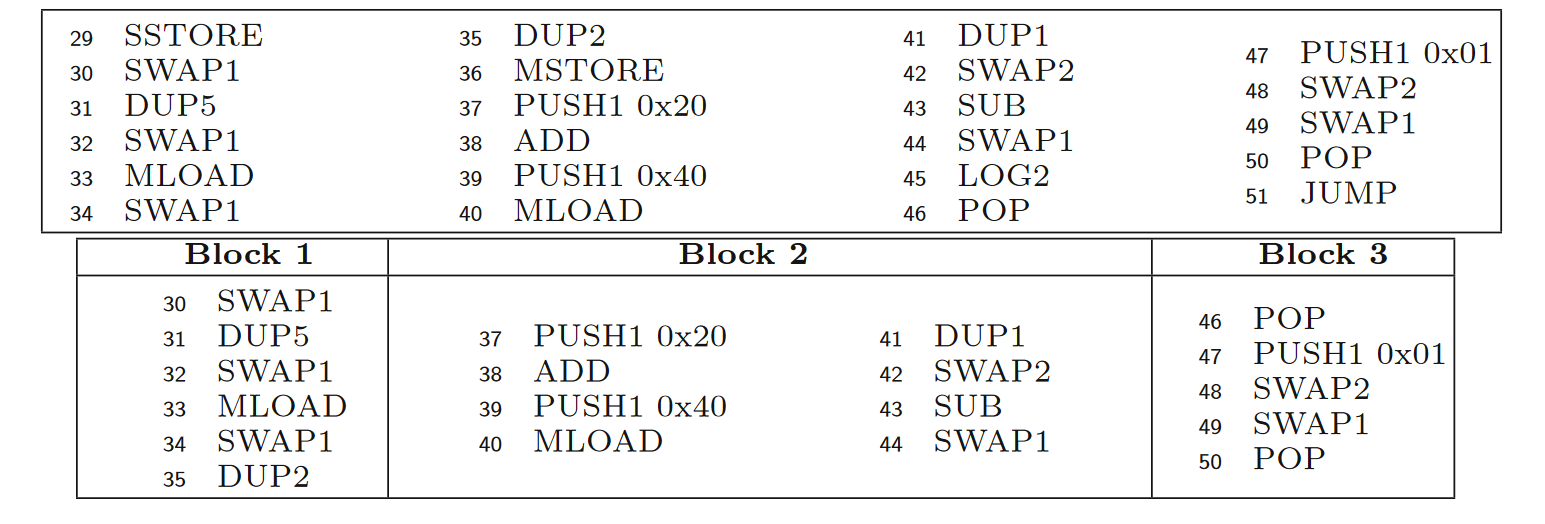
(2)SFS 的提取
在从 CFG 中获得子块后,需要使用符号执行获得输出堆栈(即执行块中字节码序列后的栈)的功能描述。由于在执行事务之前栈是空的,并且每个EVM字节码消耗和产生的元素个数已知,因此可以静态推断每个子块开始时栈的大小。规定符号栈 S S S 是一个大小为 k k k 的列表,表示栈的状态,其中列表位置 0 0 0 对应栈的顶部, k − 1 k - 1 k−1 是栈底部的索引,则 S [ i ] S [i] S[i] 是存储在栈的位置 i i i 的符号值。最初,输入栈将每个指标映射为一个符号变量 s i s_{i} si,转换函数表示为 τ \tau τ,则对栈上操作的指令进行符号执行如下:
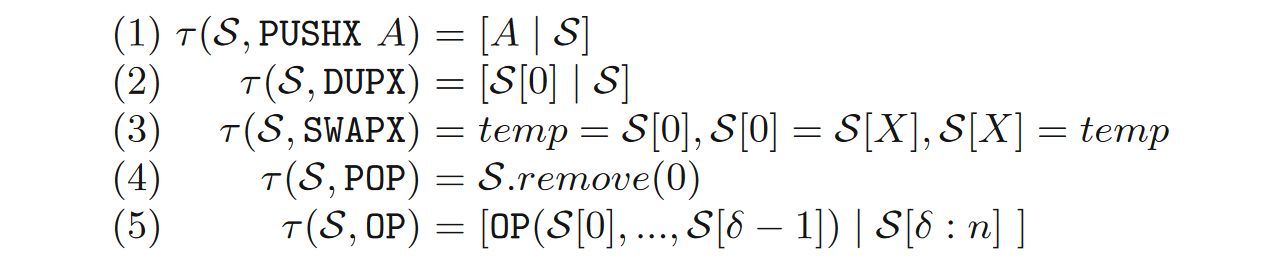
利用上述符号,可以给出 SFS 的定义为:给定一个堆栈初始大小为 k k k 的块 B B B,初始堆栈 S 0 S_{0} S0 在每个位置存储 ( i ∈ 0 , . . . , k − 1 ) (i∈{ 0,. . .,k-1 }) (i∈0,...,k−1) 一个符号变量 s i s_{i} si,然后,将传递函数 τ \tau τ 扩展到块 B B B,记为 τ ( B ) \tau (B) τ(B)。若 B B B 为空,则有 [ s 0 , … , s k − 1 ] [s_{0}, \ldots , s_{k-1}] [s0,…,sk−1];若 B B B 有 o o o 作为最后一次运算,则表示为 τ ( τ ( B ′ ) , o ) \tau\left(\tau\left(B^{\prime}\right), o\right) τ(τ(B′),o) ,其中, B ′ B' B′ 表示是没有 o o o 的结果块。依据上述定义可知, B B B 的 SFS 表示为: S 0 ⟹ S = τ ( B ) \mathcal{S}_{0} \Longrightarrow \mathcal{S}=\tau(B) S0⟹S=τ(B)。
4.2 最优字节码合成
在提取了 SFS 后,接下来需要对 SFS、栈以及指令、gas消耗进行抽象表示,利用这些抽象表示来描述优化过程中的软约束、硬约束以及目标函数,再利用 Max-SMT 实现最优字节码的合成。
(1)SFS 抽象处理
对于堆栈初始大小为 k k k 的栈有:
- 初始栈的 stack variables: [ s 0 , … , s k − 1 ] [s_{0}, \ldots, s_{k-1}] [s0,…,sk−1]
- 引入的 fresh variables: s k , s k + 1 , … s_{k}, s_{k+1}, \ldots sk,sk+1,…
- 映射关系 M M M(从 fresh variables 到由无解释的函数)
(2)堆栈模型建立
- 栈内元素抽象
为了区分栈中 { 由 Push 操作引入的常数 constant } 和 { initial stack variables 以及除 Push 操作引入的 fresh variables }(这里的区分是为了后续约束条件的表示和判断),本文规定,由 Push 操作引入的 constant 取值范围是
{
0
,
2
256
−
1
}
\{0, 2^{256}-1\}
{0,2256−1},由 initial stack variables 和 除 Push 操作引入的 fresh variables 的取值范围是:
S
V
=
⋀
0
⩽
i
<
v
s
i
=
2
256
+
i
S_{V}=\bigwedge_{0 \leqslant i<v} s_{i}=2^{256}+i
SV=0⩽i<v⋀si=2256+i
- 栈属性和操作抽象
在抽象化栈中的元素表示后,本文对栈的属性进行了符号化:
- b o b_{o} bo : 操作次数(利用启发算法 heuristics 确定)
- b s b_{s} bs : 栈的大小(利用启发算法 heuristics 确定)
- x i , j ∈ Z x_{i, j} \in \mathbb{Z} xi,j∈Z, i ∈ { 0 , … , b s − 1 } i \in \left \{0, \ldots, b_{s}-1\right\} i∈{0,…,bs−1}, j ∈ { 0 , … , b s − 1 } j \in \left \{0, \ldots, b_{s}-1\right\} j∈{0,…,bs−1} : 执行前 j j j 个操作后,栈中 i i i 位置的元素
- u i , j u_{i,j} ui,j, i ∈ { 0 , … , b s − 1 } i \in \left \{0, \ldots, b_{s}-1\right\} i∈{0,…,bs−1}, j ∈ { 0 , … , b s − 1 } j \in \left \{0, \ldots, b_{s}-1\right\} j∈{0,…,bs−1} : 执行前 j j j 个操作后,栈中第 i i i 个位置的元素是否存在
- Move ( j , α , β , δ ) = ⋀ α ⩽ i ⩽ β u i + δ , j + 1 = u i , j ∧ x i + δ , j + 1 = x i , j \operatorname{Move}(j, \alpha, \beta, \delta)=\bigwedge_{\alpha \leqslant i \leqslant \beta} u_{i+\delta, j+1}=u_{i, j} \wedge x_{i+\delta, j+1}=x_{i, j} Move(j,α,β,δ)=⋀α⩽i⩽βui+δ,j+1=ui,j∧xi+δ,j+1=xi,j : 为了简化后面的定义,本文引入了参数化约束,含义是给定一个指令 j j j, 0 < j ≤ b 0 0 \lt j \le b_{0} 0<j≤b0,两个栈位置 α α α 和 β β β 以及移位量 δ ∈ Z \delta \in \mathbb{Z} δ∈Z,有 0 ≤ α , 0 ≤ α + δ , β < b s 0 \leq \alpha, 0 \leq \alpha+\delta, \beta<b_{s} 0≤α,0≤α+δ,β<bs 和 β + δ < b s \beta+\delta<b_{s} β+δ<bs,使得在移位量为 δ \delta δ 的情况下(如果为负则向上移动,否则向下移动),位置 α α α 和 β β β 之间执行 j + 1 j + 1 j+1 条指令后的栈与执行 j j j 条指令后的栈相同。
(3)指令编码
本文将指令集 I \mathcal{I} I 划分为了三个子集 I C ⊎ I U ⊎ I S \mathcal{I}_{C} \uplus \mathcal{I}_{U} \uplus \mathcal{I}_{S} IC⊎IU⊎IS,分别表示:
- I C \mathcal{I}_{C} IC : 包含发生在抽象 SFS 的映射 M M M 中的交换无解释的函数
- I U \mathcal{I}_{U} IU : 包含发生在抽象 SFS 的映射 M M M 中的非交换无解释的函数
-
I
S
\mathcal{I}_{S}
IS : 包含栈操作:
PUSH,它在栈顶引入一个高达32字节的元素;
POP,移除栈顶部的元素;
DUPk,将栈中位于 k − 1 k - 1 k−1 的元素复制到栈的顶端,其中 k ∈ { 1 , … , 16 } k\in \{1, \ldots, 16\} k∈{1,…,16} ;
SWAPk,将栈顶部元素与栈中位于 k k k 的元素交换,其中 k ∈ { 1 , … , 16 } k\in \{1, \ldots, 16\} k∈{1,…,16} ;
NOP,额外的操作,表示什么也不做。
利用 θ \theta θ 表示从指令集 I \mathcal{I} I 到连续不同非负整数 { 0 , … , m l } \{0, \ldots, m_{l}\} {0,…,ml} 的映射,则 m l + 1 m_{l}+1 ml+1 表示指令集的基数,为了在每一步对选择的指令进行编码,本文引入了存在量化变量 t j ∈ { 0 , … , m l } , j ∈ { 0 , … , b o − 1 } t_{j} \in \{0, \ldots, m_{l}\}, j\in\{0, \ldots, b_{o}-1\} tj∈{0,…,ml},j∈{0,…,bo−1},表示对于每个指令 l ∈ I l\in \mathcal{I} l∈I 有:如果 t j = θ ( l ) t_{j} = \theta(l) tj=θ(l),则在步骤 j j j 执行的操作为 l l l。此外,本文引入了相关的存在量化变量 a j ∈ { 0 , … , 2 256 − 1 } a_{j}\in\{0, \ldots, 2^{256}-1\} aj∈{0,…,2256−1},其中 j ∈ { 0 , … , b o − 1 } j\in\{0, \ldots, b_{o}-1\} j∈{0,…,bo−1},表示当 t j = θ ( P U S H ) t_{j}=\theta(PUSH) tj=θ(PUSH) 时堆栈顶端的值,否则 a j a_{j} aj 的值无意义。在定义了需要的符号表示后,本文开始对优化过程的约束条件进行定义。
Encoding the Stack Operations
C
P
U
S
H
(
j
)
=
t
j
=
θ
(
P
U
S
H
)
⇒
0
≤
a
j
<
2
256
∧
¬
u
b
s
−
1
,
j
∧
u
0
,
j
+
1
∧
x
0
,
j
+
1
=
a
j
∧
Move
(
j
,
0
,
b
s
−
2
,
1
)
C
D
U
P
k
(
j
)
=
t
j
=
θ
(
D
U
P
k
)
⇒
¬
u
b
s
−
1
,
j
∧
u
k
−
1
,
j
∧
u
0
,
j
+
1
∧
x
0
,
j
+
1
=
x
k
−
1
,
j
∧
Move
(
j
,
0
,
b
s
−
2
,
1
)
C
S
W
A
P
k
(
j
)
=
t
j
=
θ
(
SWAP
k
)
⇒
u
k
,
j
∧
u
0
,
j
+
1
∧
x
0
,
j
+
1
=
x
k
,
j
∧
u
k
,
j
+
1
∧
x
k
,
j
+
1
=
x
0
,
j
∧
Move
(
j
,
1
,
k
−
1
,
0
)
∧
Move
(
j
,
k
+
1
,
b
s
−
1
,
0
)
C
P
O
P
(
j
)
=
t
j
=
θ
(
P
O
P
)
⇒
u
0
,
j
∧
¬
u
b
s
−
1
,
j
+
1
∧
Move
(
j
,
1
,
b
s
−
1
,
−
1
)
C
N
O
P
(
j
)
=
t
j
=
θ
(
N
O
P
)
⇒
Move
(
j
,
0
,
b
s
−
1
,
0
)
\begin{array}{l} C_{\mathrm{PUSH}}(j)=t_{j}=\theta(\mathrm{PUSH}) \Rightarrow 0 \leq a_{j}<2^{256} \wedge \neg u_{b_{s}-1, j} \wedge u_{0, j+1} \wedge x_{0, j+1} \\ =a_{j} \wedge \text {Move}\left(j, 0, b_{s}-2,1\right) \\ C_{\mathrm{DUP} k}(j)=t_{j}=\theta(\mathrm{DUP} k) \Rightarrow \neg u_{b_{s}-1, j} \wedge u_{k-1, j} \wedge u_{0, j+1} \wedge x_{0, j+1}=x_{k-1, j} \wedge \\ \operatorname{Move}\left(j, 0, b_{s}-2,1\right) \\ C_{\mathrm{SWAP} k}(j)=t_{j}=\theta(\operatorname{SWAP} k) \Rightarrow u_{k, j} \wedge u_{0, j+1} \wedge x_{0, j+1}=x_{k, j} \wedge u_{k, j+1} \wedge \\ x_{k, j+1}=x_{0, j} \wedge \operatorname{Move}(j, 1, k-1,0) \wedge \operatorname{Move}\left(j, k+1, b_{s}-1,0\right) \\ C_{\mathrm{POP}}(j)=t_{j}=\theta(\mathrm{POP}) \Rightarrow u_{0, j} \wedge \neg u_{b_{s}-1, j+1} \wedge \operatorname{Move}\left(j, 1, b_{s}-1,-1\right) \\ C_{\mathrm{NOP}}(j)=t_{j}=\theta(\mathrm{NOP}) \Rightarrow \operatorname{Move}\left(j, 0, b_{s}-1,0\right) \end{array}
CPUSH(j)=tj=θ(PUSH)⇒0≤aj<2256∧¬ubs−1,j∧u0,j+1∧x0,j+1=aj∧Move(j,0,bs−2,1)CDUPk(j)=tj=θ(DUPk)⇒¬ubs−1,j∧uk−1,j∧u0,j+1∧x0,j+1=xk−1,j∧Move(j,0,bs−2,1)CSWAPk(j)=tj=θ(SWAPk)⇒uk,j∧u0,j+1∧x0,j+1=xk,j∧uk,j+1∧xk,j+1=x0,j∧Move(j,1,k−1,0)∧Move(j,k+1,bs−1,0)CPOP(j)=tj=θ(POP)⇒u0,j∧¬ubs−1,j+1∧Move(j,1,bs−1,−1)CNOP(j)=tj=θ(NOP)⇒Move(j,0,bs−1,0)
当 NOP 出现在中间步骤时,为了避免冗余解,本文还增加了一个约束,即一旦选择 NOP 作为指令
t
j
t_{j}
tj,之后只能选择 NOP 作为接下来的指令
t
j
+
1
,
t
j
+
2
,
…
t_{j}+1, t_{j} + 2, \ldots
tj+1,tj+2,…(因为 NOP 表示什么都不做,所以类似提前结束):
C
fromNOP
=
⋀
0
⩽
j
<
b
o
−
1
t
j
=
θ
(
N
O
P
)
⇒
t
j
+
1
=
θ
(
N
O
P
)
C_{\text {fromNOP }}=\bigwedge_{0 \leqslant j<b_{o}-1} t_{j}=\theta(\mathrm{NOP}) \Rightarrow t_{j+1}=\theta(\mathrm{NOP})
CfromNOP =0⩽j<bo−1⋀tj=θ(NOP)⇒tj+1=θ(NOP)
Encoding the Uninterpreted Operations
无解释的操作编码来自抽象后的 S F S SFS SFS 的映射 M M M,如前文所述,每个函数 f f f 在 M M M 中只出现一次,且对于 M M M 中的每一个 r ↦ f ( o 0 , … , o n − 1 ) r \mapsto f\left(o_{0}, \ldots, o_{n-1}\right) r↦f(o0,…,on−1),有 f ∈ I C ⊎ I U f \in \mathcal{I}_{C} \uplus \mathcal{I}_{U} f∈IC⊎IU, r r r 为新变量, o 0 , … , o n − 1 o_{0}, \ldots, o_{n-1} o0,…,on−1 为初始堆栈变量、新变量或常数。另外,对于 f ∈ I C f\in \mathcal{I}_{C} f∈IC,由于涉及交换操作,所以有 n = 2 n=2 n=2。这些抽象表示对应的具体过程是,当遇到无解释操作函数时,利用操作数 o 0 , … , o n − 1 o_{0}, \ldots, o_{n-1} o0,…,on−1 ( o 0 o_{0} o0 表示栈顶元素)操作得到结果 r r r,再将 r r r 存放于栈顶。对应的约束条件表示如下:
C U ( j , f ) = t j = θ ( f ) ⇒ ⋀ 0 ⩽ i ⩽ n − 1 ( u i , j ∧ x i , j = o i ) ∧ u 0 , j + 1 ∧ x 0 , j + 1 = r ∧ Move ( j , n , min ( b s − 2 + n , b s − 1 ) , 1 − n ) ∧ ⋀ b s − n + 1 ⩽ i ⩽ b s − 1 ¬ u i , j + 1 C C ( j , f ) = t j = θ ( f ) ⇒ u 0 , j ∧ u 1 , j ∧ ( ( x 0 , j = o 0 ∧ x 1 , j = o 1 ) ∨ ( x 0 , j = o 1 ∧ x 1 , j = o 0 ) ) ∧ u 0 , j + 1 ∧ x 0 , j + 1 = r ∧ Move ( j , 2 , b s − 1 , − 1 ) ∧ ¬ u b s − 1 , j \begin{aligned} C_{U}(j, f)=t_{j}=\theta(f) \Rightarrow & \bigwedge_{0 \leqslant i \leqslant n-1}\left(u_{i, j} \wedge x_{i, j}=o_{i}\right) \wedge u_{0, j+1} \wedge x_{0, j+1}=r \wedge \\ & \operatorname{Move}\left(j, n, \min \left(b_{s}-2+n, b_{s}-1\right), 1-n\right) \wedge \\ & \bigwedge_{b_{s}-n+1 \leqslant i \leqslant b_{s}-1} \neg u_{i, j+1} \\ C_{C}(j, f)=t_{j}=\theta(f) \Rightarrow & u_{0, j} \wedge u_{1, j} \wedge \\ & \left(\left(x_{0, j}=o_{0} \wedge x_{1, j}=o_{1}\right) \vee\left(x_{0, j}=o_{1} \wedge x_{1, j}=o_{0}\right)\right) \wedge \\ & u_{0, j+1} \wedge x_{0, j+1}=r \wedge \operatorname{Move}\left(j, 2, b_{s}-1,-1\right) \wedge \neg u_{b_{s}-1, j} \end{aligned} CU(j,f)=tj=θ(f)⇒CC(j,f)=tj=θ(f)⇒0⩽i⩽n−1⋀(ui,j∧xi,j=oi)∧u0,j+1∧x0,j+1=r∧Move(j,n,min(bs−2+n,bs−1),1−n)∧bs−n+1⩽i⩽bs−1⋀¬ui,j+1u0,j∧u1,j∧((x0,j=o0∧x1,j=o1)∨(x0,j=o1∧x1,j=o0))∧u0,j+1∧x0,j+1=r∧Move(j,2,bs−1,−1)∧¬ubs−1,j
其中:
f ∈ I U and r ↦ f ( o 0 , … , o n − 1 ) ∈ M f ∈ I C and r ↦ f ( o 0 , o 1 ) ∈ M \begin{aligned} f \in \mathcal{I}_{U} \text { and } r \mapsto f\left(o_{0}, \ldots, o_{n-1}\right) \in M \\ f \in \mathcal{I}_{C} \text { and } r \mapsto f\left(o_{0}, o_{1}\right) \in M \end{aligned} f∈IU and r↦f(o0,…,on−1)∈Mf∈IC and r↦f(o0,o1)∈M
Finding the Target Program
由上述约束条件可得,指令集 I \mathcal{I} I 对应的约束条件为:
C
I
=
C
fromnop
∧
⋀
0
⩽
j
<
b
o
0
≤
t
j
≤
m
ι
∧
C
P
U
S
H
(
j
)
∧
C
D
U
P
k
(
j
)
∧
C
S
W
A
P
k
(
j
)
∧
C
P
O
P
(
j
)
∧
C
N
O
P
(
j
)
∧
⋀
f
∈
I
U
C
U
(
j
,
f
)
∧
⋀
f
∈
I
C
C
C
(
j
,
f
)
)
\begin{array}{l} C_{\mathcal{I}}=C_{\text {fromnop }} \wedge \bigwedge_{0 \leqslant j<b_{o}} 0 \leq t_{j} \leq m_{\iota} \wedge \\ C_{\mathrm{PUSH}}(j) \wedge C_{\mathrm{DUP} k}(j) \wedge C_{\mathrm{SWAP} k}(j) \wedge C_{\mathrm{POP}}(j) \wedge \\ \left.C_{\mathrm{NOP}}(j) \wedge \bigwedge_{f \in \mathcal{I}_{U}} C_{U}(j, f) \wedge \bigwedge_{f \in \mathcal{I}_{C}} C_{C}(j, f)\right) \\ \end{array}
CI=Cfromnop ∧⋀0⩽j<bo0≤tj≤mι∧CPUSH(j)∧CDUPk(j)∧CSWAPk(j)∧CPOP(j)∧CNOP(j)∧⋀f∈IUCU(j,f)∧⋀f∈ICCC(j,f))
Complete Encoding
由于 C S F S C_{SFS} CSFS 描述了为给定的初始栈 [ s 0 , … , s k − 1 ] [ s_{0}, \ldots, s_{k-1}] [s0,…,sk−1] 找到一个EVM块的整个问题,并通过最终栈 [ f 0 , … , f w − 1 ] [f_{0} , \ldots , f_{w-1}] [f0,…,fw−1] 和 M M M 抽象出 SFS。因此,这里引入一个约束 B B B 来描述堆栈在开始时的情况,引入一个约束 E E E 来描述堆栈在结束时的情况,并结合前面定义的所有约束来表示 C S F S C_{SFS} CSFS:
B = ⋀ 0 ⩽ α < k ( u α , 0 ∧ x α , 0 = s α ) ∧ ⋀ k ⩽ β ⩽ b s − 1 ¬ u β , 0 E = ⋀ 0 ⩽ α < w ( u α , b o ∧ x α , b o = f α ) ∧ ⋀ w ⩽ β ⩽ b s − 1 ¬ u β , b o C S F S = S V ∧ C I ∧ B ∧ E \begin{array}{l} B=\bigwedge_{0 \leqslant \alpha<k}\left(u_{\alpha, 0} \wedge x_{\alpha, 0}=s_{\alpha}\right) \wedge \bigwedge_{k \leqslant \beta \leqslant b_{s}-1} \neg u_{\beta, 0} \\ E \quad=\bigwedge_{0 \leqslant \alpha<w}\left(u_{\alpha, b_{o}} \wedge x_{\alpha, b_{o}}=f_{\alpha}\right) \wedge \bigwedge_{w \leqslant \beta \leqslant b_{s}-1} \neg u_{\beta, b_{o}} \\ C_{S F S}=S_{V} \wedge C_{\mathcal{I}} \wedge B \wedge E \end{array} B=⋀0⩽α<k(uα,0∧xα,0=sα)∧⋀k⩽β⩽bs−1¬uβ,0E=⋀0⩽α<w(uα,bo∧xα,bo=fα)∧⋀w⩽β⩽bs−1¬uβ,boCSFS=SV∧CI∧B∧E
另外,本文添加了一条额外的约束来提高效率: ⋀ ι ∈ I U ⊎ I C ⋁ 0 ⩽ j < b o t j = θ ( ι ) \bigwedge_{\iota \in \mathcal{I}_{U} \uplus \mathcal{I}_{C}} \bigvee_{0 \leqslant j<b_{o}} t_{j}=\theta(\iota) ⋀ι∈IU⊎IC⋁0⩽j<botj=θ(ι)
(4)操作提取
这里论文展示了如何从计算给定 C S F S C_{SFS} CSFS 模型中提取一组具体的操作,具体定义为:给定一个 C S F S C_{SFS} CSFS 模型 σ \sigma σ,定义 b l o c k ( σ ) block(\sigma) block(σ) 为 EVM 运算序列 o 0 , … , o f o_{0},\ldots, o_{f} o0,…,of,其中 f f f 是最大的 j ∈ { 0 , … , b o − 1 } j\in\{0, \ldots, b_{o-1}\} j∈{0,…,bo−1} 且使得 t j = θ ( N O P ) t_{j}=\theta( NOP) tj=θ(NOP),现在对所有的 α ∈ { 0 , … , f } \alpha\in\{0,\ldots, f\} α∈{0,…,f}, o α o_{\alpha} oα取为:
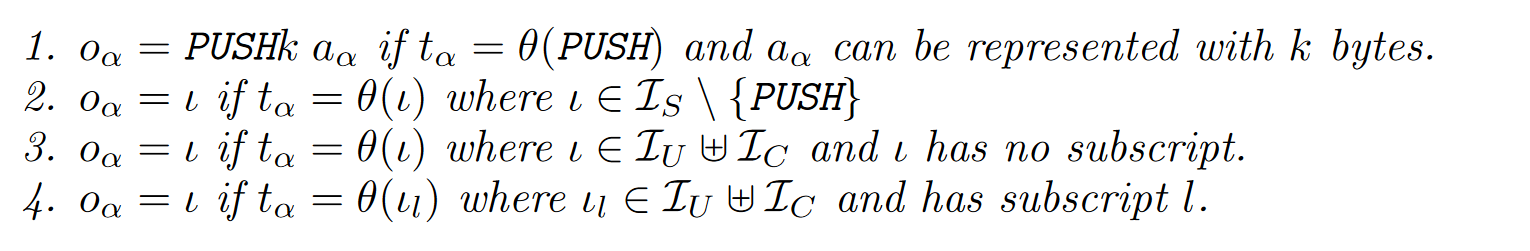
这些取值的选择将服从之前定义的 C S F S C_{SFS} CSFS 约束条件,利用约束条件和操作提取的选择,可以建立所有满足条件的运算序列,即多个 b l o c k ( σ ) block(\sigma) block(σ)。
(5)Max-SMT 优化
一个(部分加权) Max-SMT 问题是一个优化问题,其中有一个 SMT 公式,表示建立问题的硬约束和一组对 { [ C 1 , ω 1 ] , … , [ C m , ω m ] } \left\{\left[C_{1}, \omega_{1}\right], \ldots,\left[C_{m}, \omega_{m}\right]\right\} {[C1,ω1],…,[Cm,ωm]},每个 C i C_{i} Ci 是 SMT 子句, ω i \omega_{i} ωi 是其权重,以此建立软约束。
在获取了多个 b l o c k ( σ ) block(\sigma) block(σ) 后,需要从中选择一个最优的运算序列(最优字节码),由于求解的成本可以用在所有 t j t_{j} tj 中选择的每个指令的成本来表示,因此本文引入了表示每个选择成本的软约束,再结合前文的约束条件构成的硬约束,建立 Max-SMT优化问题,并以消耗最少 gas 为目标函数,进行最优合成字节码的求解。
在这个过程中,需要注意的是,在EVM中,每个操作都有一个相关的 gas 成本,一般情况下是恒定的,但在某些情况下可能取决于它应用到的特定参数或区块链的状态。所有这些非常数的操作都被认为是无解释的,不能改变它们所应用的操作数。而省略非常数部分不会影响哪个是最优解,因此,可以将指令集 I \mathcal{I} I 拆分成 p + 1 p + 1 p+1 个不交集 W 0 ⊎ … ⊎ W p W_{0} \uplus \ldots \uplus W_{p} W0⊎…⊎Wp,其中 W i W_{i} Wi 中的所有指令的成本 c o s t i cost_{i} costi 是恒定的常数,并且使得成本严格递增,即 c o s t 0 = 0 cost_{0} = 0 cost0=0 且 c o s t i − 1 < c o s t i , i ∈ { 1 , … , p } cost_{i - 1} \lt cost_{i}, i \in \{1,\ldots,p\} costi−1<costi,i∈{1,…,p}。另外,设 ω i = c o s t i − c o s t i − 1 , i ∈ { 1 , … , p } \omega_{i} = cost_{i}-cost_{i-1}, i\in\{1,\ldots,p\} ωi=costi−costi−1,i∈{1,…,p} ,则有 c o s t i = ∑ 1 ⩽ α ⩽ i w α , i ∈ { 1 , … p } cost_{i}=\sum_{1 \leqslant \alpha \leqslant i} w_{\alpha},i\in\{1,\ldots\,p\} costi=∑1⩽α⩽iwα,i∈{1,…p},然后,在 C S F S C_{SFS} CSFS 中加入软约束,得到 Max - SMT 问题 O S F S O_{SFS} OSFS:
O
S
F
S
=
C
S
F
S
∧
⋀
0
⩽
j
<
b
o
⋀
1
⩽
i
⩽
p
[
⋁
ι
∈
W
0
⊎
…
⊎
W
i
−
1
t
j
=
θ
(
ι
)
,
w
i
]
O_{S F S}=C_{S F S} \wedge \bigwedge_{0 \leqslant j<b_{o}} \bigwedge_{1 \leqslant i \leqslant p}\left[\bigvee_{\iota \in W_{0} \uplus \ldots \uplus W_{i-1}} t_{j}=\theta(\iota), w_{i}\right]
OSFS=CSFS∧0⩽j<bo⋀1⩽i⩽p⋀
ι∈W0⊎…⊎Wi−1⋁tj=θ(ι),wi
因此,如果在第
j
j
j 步选择的指令为
l
,
t
j
=
θ
(
ι
)
l, t_{j} = \theta(ι)
l,tj=θ(ι),对于
l
∈
W
i
l\in W_{i}
l∈Wi,可以累积所有
α
∈
{
1
,
…
,
i
}
\alpha\in \{1,\ldots,i \}
α∈{1,…,i}的软子句权重
ω
α
\omega_{\alpha}
ωα,并记为
c
o
s
t
i
cost_{i}
costi,从而累积执行指令
ι
ι
ι 的代价。
相关概念
-
Ethereum Virtual Machine(EVM,以太坊虚拟机)
EVM 用于运行以太坊开发者编写的智能合约,EVM 是一种简单的基于堆栈的体系结构,即 EVM 的计算基于堆栈的字节码语言完成,机器的字大小为256位( 32字节),这也是堆栈项的大小。 -
Basic block(基本块)
一个由一系列指令组成的基本块,其中间没有任何 JUMP 操作。 -
Gas (燃料)
成功进行交易或执行智能合约所需的费用或价值,gas 消耗主要来自每个EVM指令所对应的计算和存储成本。其中,计量 gas 的原理是三重的:
(1)执行 gas 计量时对事务能够执行的操作数量进行限制,防止基于非终止执行的攻击;
(2)不允许提议者在创建交易并支付 gas 时浪费其他方(也就是矿工)的计算资源;
(3)gas 费用阻碍了用户过度使用复制存储,因为复制存储是基于区块链的共识系统中宝贵的资源。 -
Super-optimization(超优化)
超优化是一种通过尝试所有可能产生相同结果的指令序列来寻找代码块的最佳翻译的技术。 -
Stack functional specification(SFS,栈功能规范)
SFS 是对进入块时的初始堆栈和执行块后的最终堆栈的功能描述,它通过对初始堆栈元素的符号一阶项来定义,而不是使用字节码指令来确定最终堆栈是如何计算的。
参考文献
[
1
]
[1]
[1] Jangda, A., Yorsh, G.: Unbounded superoptimization. In: Proceedings of the 2017 ACM SIGPLAN International Symposium on New Ideas, New Paradigms, and Reflections on Programming and Software, Onward! 2017, Vancouver, BC, Canada, 23–27 October 2017, pp. 78–88 (2017)
[
2
]
[2]
[2] Mesnard, F., Stuckey, P.J. (eds.): LOPSTR 2018. LNCS, vol. 11408. Springer, Cham (2019). https://doi.org/10.1007/978-3-030-13838-7
[
3
]
[3]
[3] Wood, G.: Ethereum: a secure decentralised generalised transaction ledger (2019)






















 465
465











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








