Bézier curve(贝塞尔曲线)是应用于二维图形应用程序的数学曲线。 曲线定义:起始点、终止点(也称锚点)、控制点。通过调整控制点,贝塞尔曲线的形状会发生变化。 1962年,法国数学家Pierre Bézier第一个研究了这种矢量绘制曲线的方法,并给出了详细的计算公式,因此按照这样的公式绘制出来的曲线就用他的姓氏来命名,称为贝塞尔曲线。
以下公式中:B(t)为t时间下 点的坐标;
P0为起点,Pn为终点,Pi为控制点
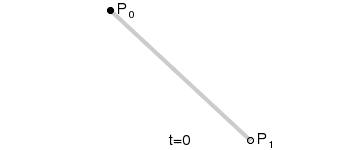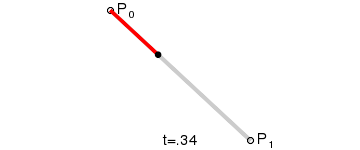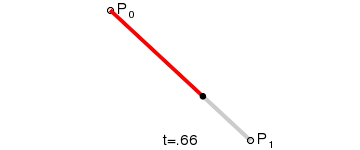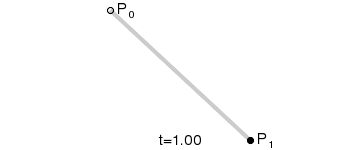
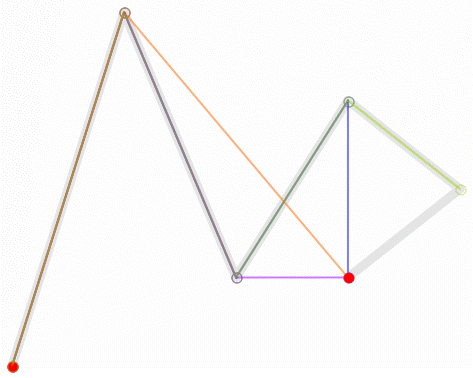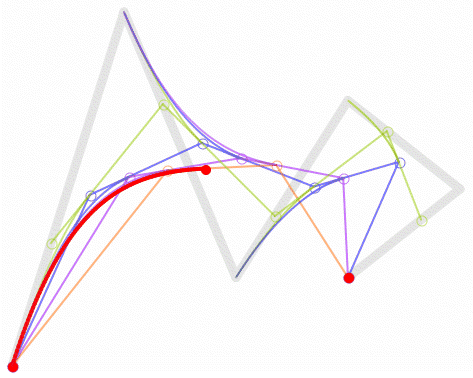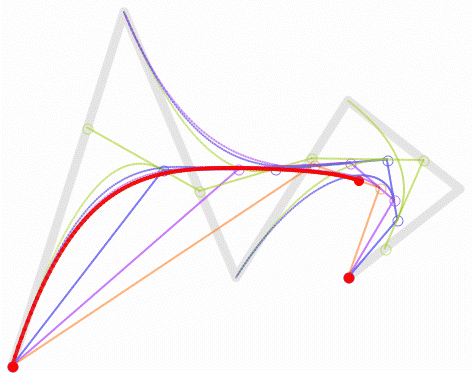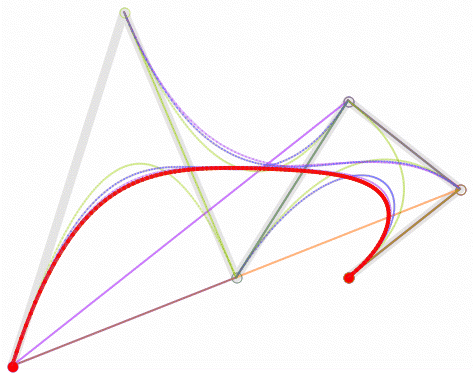
一阶贝塞尔曲线(线段):
意义:由 P0 至 P1 的连续点, 描述的一条线段
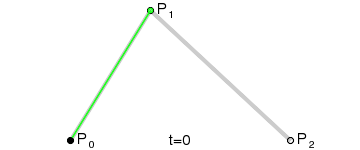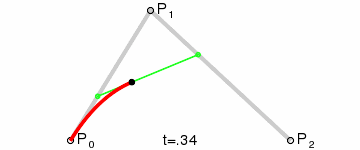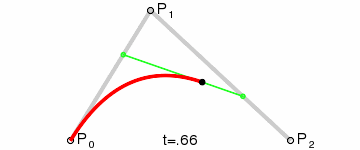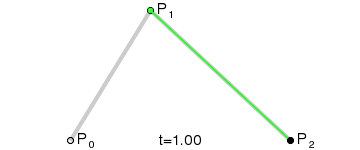
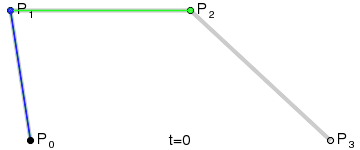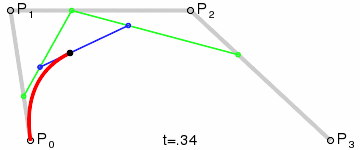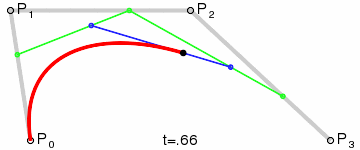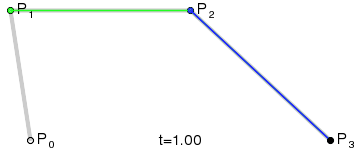
二阶贝塞尔曲线(抛物线):
原理:由 P0 至 P1 的连续点 Q0,描述一条线段。
由 P1 至 P2 的连续点 Q1,描述一条线段。
由 Q0 至 Q1 的连续点 B(t),描述一条二次贝塞尔曲线。
经验:P1-P0为曲线在P0处的切线。
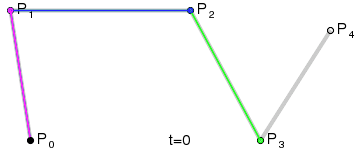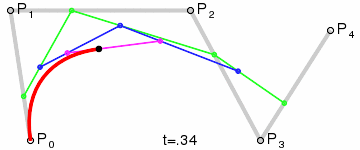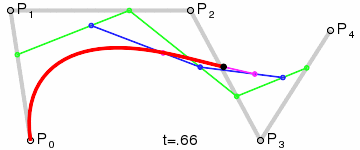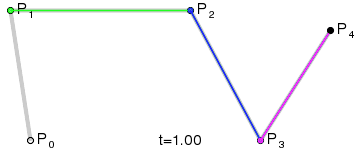
三阶贝塞尔曲线:
通用公式:
高阶贝塞尔曲线:
4阶曲线:
5阶曲线:
http://www.cs.mtu.edu/~shene/COURSES/cs3621/NOTES/spline/Bezier/de-casteljau.html
三次贝塞尔曲线光滑示例:
struct D_DOT3D //D_DOT3D的主要参数,未完全实现
{
double x,y,z;
}
double GetThreeBezierValue(double p0, double p1, double p2, double p3, double t)
{
return pow(1-t,3.0) * p0 + 3*t*(1-t)*(1-t)*p1 + 3*t*t*(1-t)*p2 + t*t*t*p3;
}
D_DOT3D GetThreeBezierValue(D_DOT3D p0, D_DOT3D p1, D_DOT3D p2, D_DOT3D p3 , double t)
{
D_DOT3D dot;
dot.x = GetThreeBezierValue(p0.x, p1.x, p2.x, p3.x, t);
dot.y = GetThreeBezierValue(p0.y, p1.y, p2.y, p3.y, t);
dot.z = GetThreeBezierValue(p0.z, p1.z, p2.z, p3.z, t);
return dot;
}
long ThreeBezierCurve( vector<D_DOT3D> &line )
{
if (line.size()<4)
return 0;
vector<D_DOT3D> vout;
for (int i=0; i<line.size()-3; i += 3)
{
D_DOT3D p0(line[i]);
D_DOT3D p1(line[i+1]);
D_DOT3D p2(line[i+2]);
D_DOT3D p3(line[i+3]);
if (0 == i)
{
D_DOT3D dot1 = GetThreeBezierValue(p0, p1, p2, p3, 0.);
vout.push_back(dot1);
}
D_DOT3D dot2 = GetThreeBezierValue(p0, p1, p2, p3, 1/3.0);
D_DOT3D dot3 = GetThreeBezierValue(p0, p1, p2, p3, 2/3.0);
D_DOT3D dot4 = GetThreeBezierValue(p0, p1, p2, p3, 1.0);
vout.push_back(dot2);
vout.push_back(dot3);
vout.push_back(dot4);
}
line = vout;
return 1;
}






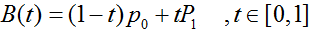
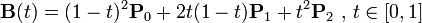
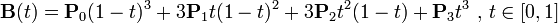
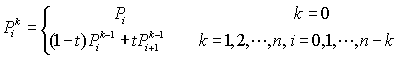














 1645
1645

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








