转自:http://www.mamicode.com/info-detail-874778.html
CNN公式推导
1 前言
在看此blog之前,请确保已经看懂我的前两篇blog【深度学习笔记1(卷积神经网络)】和【BP算法与公式推导】。并且已经看过文献[1]的论文【Notes on Convolutional Neural Networks】。因为本文就是讲解文献[1]论文前部分公式的推导过程<这里有一个假设,或许公式是错误的,如有好的理解请留言>。
2 CNN公式推导
卷积神经网络参数求解的过程与上次笔记【BP算法与公式推导】类似,但是在形式上还是有变化的。文献[1]的论文直接给出了参数求解的公式,主要包括:卷积层和subsampling层的残差以及对应的对权重参数和偏置参数的导数。
注意:这里的卷积核参数所放在的层与残差放在了同一层,和上次笔记略有不同,但是没有影响!
2.1 卷积层:
2.1.1 卷积计算
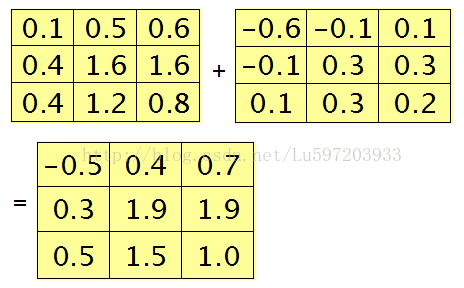
假设第l层为卷积层,第l+1层为subsampling层,则第l层第j个feature map的计算公式如下:
上面的*号实质是让卷积核k在第l-1层所有关联的feature maps上做卷积运算,然后求和,再加上一个偏置参数,取sigmoid得到最终激励值的过程。
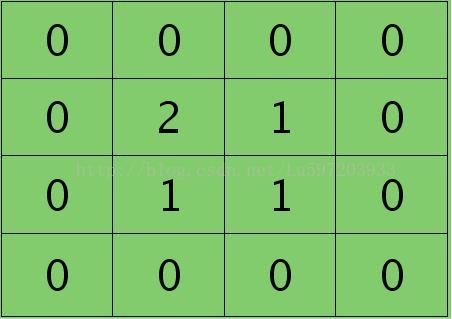
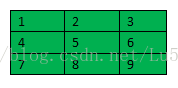
例子:假设第l-1层只有两个feature map,大小为4*4像素。
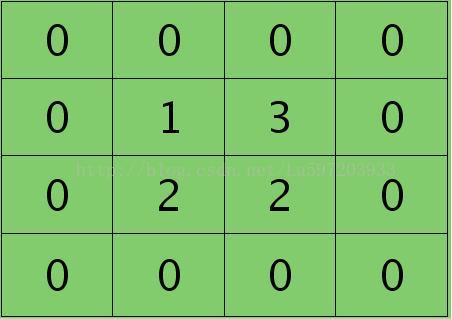
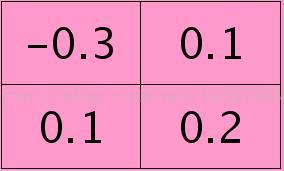
一个卷积核K(二维卷积核K11和K12),大小为2*2。
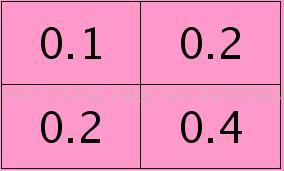
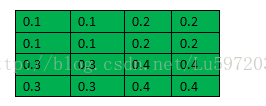
则计算第l层的一个feature map结果如下,大小为3*3像素:
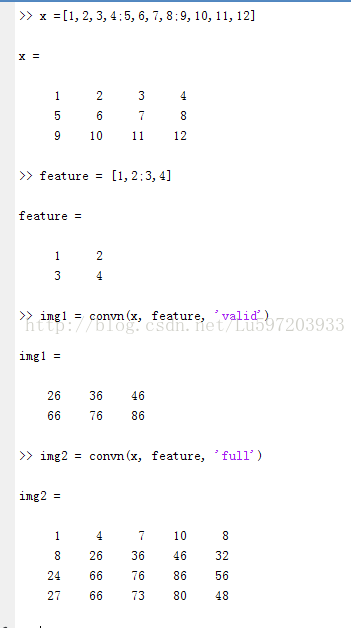
注意:在matlab中可以用convn函数来实现卷积,如:
image = convn(im, kernel, ‘valid’); 其中计算的过程会先将kernel反转180度,再与im做卷积操作。
因此本文中我们举例子用的卷积核2*2大小是已经旋转180度后的,即
2.1.2 残差计算
BP算法中残差计算等于第l+1层与其连接的所有结点的权值和残差的加权和再乘以该点对z的导数值。卷积层的下一层是subsampling层,采用的是一对一非重叠采样,故残差计算更为简单。
第l层第j个feature map的残差计算公式如下:
其中第l层为卷积层,第l+1层为subsampling层,subsampling层与卷积层是一一对应的。其中up(x)是将第l+1层的大小扩展为和第l层大小一样。举个简单的例子,假如第l+1层为2*2的,subsampling的采样大小为2*2,其中第l+1层的一个feature map所对应的残差为:

那么扩展之后就变为了
直观上的理解:由于是一对一采样,故扩展之后第l层的每个节点只对应第l+1层唯一的一个结点,按照BP算法残差计算公式可以得出:第l层某结点残差就等于权值w乘以第l+1层对应节点残差值再乘以f(z)的导数,公式仅仅是矢量化的形式。
2.1.3 梯度计算
(1) 论文中给出了偏置参数b的导数,公式为:
下面我们给出推导公式,(其中第2行到第3行用到了假设,因为这里的zjl和bjl都是矩阵,没有矩阵对矩阵求导,这里给出了一个求和公式。我也解释不了是否正确,有知道的可以留言!)其中njl为第l层第j个feature map中点的个数。
(2) 论文中给出了偏置参数k的导数,其中kijl表示第l层第j个feature map与第l-1层第i个feature map相连所对应的kernel,是一个矩阵:
公式推导如下:
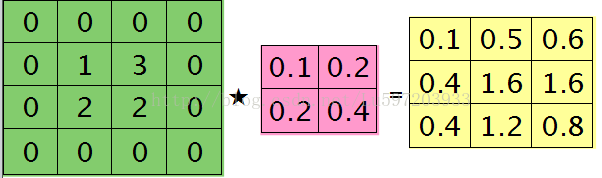
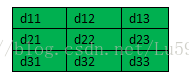
这里我们给出例子:比如卷积层为3*3的大小,卷积核的大小为2*2上一层feature map大小为4*4
论文中给出其matlab代码:
由于matlab中先要反转180度,故代码中先对残差旋转180度,得到的结果是
2.2 subsampling层:
2.2.1卷积计算
设第l层为subsampling层,第l-1为卷积层,由于是一对一采样,假设采样大小为2*2,故计算公式为:
这里的down(x)是将x中2*2的大小中像素值进行求和。计算过程为对上一层卷积层2*2大小进行求和然后乘以权重w,再加上一个偏置,再求取sigmoid函数。
2.2.2 残差计算
论文中给出了残差的计算公式:
其中第l层为subsampling层,第l+1层为卷积层。
直观上的理解:如下图:左边为subsampling层的一个featuremap,右边是卷积层的一个feature map,
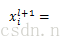
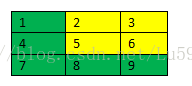
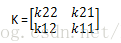 直接在下一层卷积层的残差上做卷积运算,方式为full类型,也就得到公式中的形式,由于matlab自带的卷积函数会先旋转对K旋转180度,故我们需要先对其旋转180度,再计算卷积。(当然我认为这里的公式有点偏差,的下标不应该用j,而是用i,而且需要对第l+1层中所有的与该subsampling相连接的featuremap最后的结果求和—源码中的确是这样的。)
直接在下一层卷积层的残差上做卷积运算,方式为full类型,也就得到公式中的形式,由于matlab自带的卷积函数会先旋转对K旋转180度,故我们需要先对其旋转180度,再计算卷积。(当然我认为这里的公式有点偏差,的下标不应该用j,而是用i,而且需要对第l+1层中所有的与该subsampling相连接的featuremap最后的结果求和—源码中的确是这样的。)
2.2.2 梯度计算
(1) 偏置b的导数,其公式的推导过程与卷积层是一样的的。
(2) 权重w的导数,论文给出的公式如下:
公式推导如下:
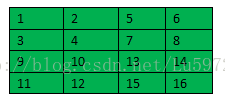
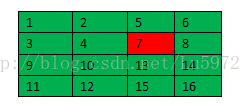
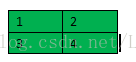
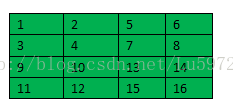
这里我们给出一个例子:比如subsampling层feature map大小为2*2,则其上一层卷积层feature map的大小为4*4,如下所示,计算过程为对上一层卷积层2*2大小进行求和然后乘以权重w,再加上一个偏置,再求取sigmoid函数。(其中1,2,3,4只是一个标号,不是具体的值)
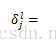

wjl = d11*{1+2+3+4} +d12*{5+6+7+8} + d21*{9+10+11+12} + d22*{13+14+15+16}。与公式相符。
注意:公式推导中有一个不那么正确的假设,但有了这个假设,一切结论都是成立的,这个结论或许超出了我数学的海拔高度,有正确解法的可以留言,谢谢!
参考文献:
1:原始论文:Notes onConvolutional Neural Networks http://cogprints.org/5869/1/cnn_tutorial.pdf
2: 论文翻译参看:http://blog.csdn.net/zouxy09/article/details/9993371
3:如何正确使用论文中公式(附带小例子)见:http://www.cnblogs.com/tornadomeet/p/3468450.html










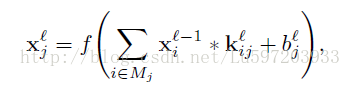
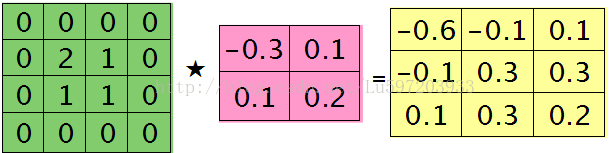
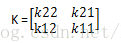
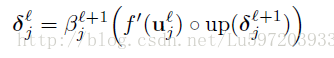
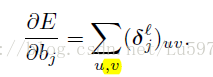
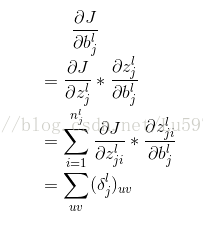
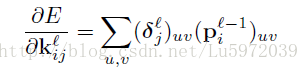
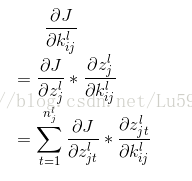
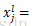
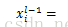
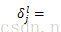
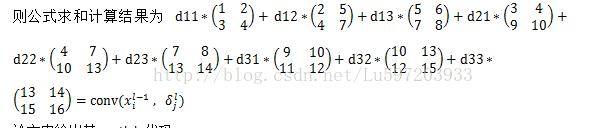
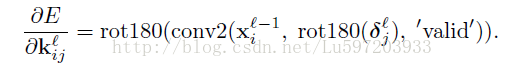
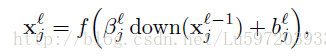
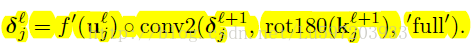
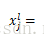
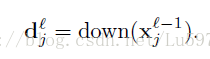
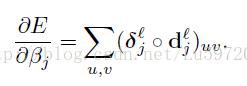
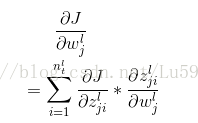
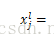
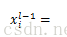














 6957
6957

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








