一.简介
SVM主要针对小样本数据进行学习、分类和预测(有时也叫回归)的一种方法,能解决神经网络不能解决的过学习问题,而且有很好的泛化能力。SVM是一种有监督的学习模型,在处理二分类问题上可以说是现有算法中的最好的一种。很多正统的算法都是从VC维理论和结构风险最小原理出发,从而引出SVM,但是对于统计理论基础不是很好的人来说理解起来比较困难,本文从线性可分情况开始,利用几何知识和数学中的约束优化方法解决分类问题。然后引申到线性不可分的情况,再来理解基于内积核的最优超平面构造方法。希望有助于大家对算法的理解。
二.线性可分情况下的SVM理解
线性可分数据的二值分类机理:系统随机产生一个超平面并移动它,直到训练集中属于不同类别的样本点正好位于该超平面的两侧。显然,这种机理能够解决线性分类问题,但不能够保证产生的超平面是最优的。支持向量机建立的分类超平面能够在保证分类精度的同时,使超平面两侧的空白区域最大化,从而实现对线性可分问题的最优分类。
支持向量机(Support Vector Machine,SVM)中的“机(machine,机器)”:实际上是一个算法。在机器学习领域,常把一些算法看作是一个机器(又叫学习机器,或预测函数,或学习函数)。
“支持向量”:是指训练集中的某些训练点,这些点最靠近分类决策面,是最难分类的数据点 。
“最优超平面”: 考虑P个线性可分样本{(X1,d1),(X2,d2
),…,(Xp,
),…(Xp,
)},对于任一输入样本Xp ,期望输出为
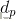
的超平面方程为
X+b=0 (1)
式中,X为输入向量,W为权值向量,b为偏置(相当于前述负阈值),则有
X+b>0
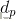
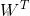
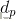
超平面与最近的样本点之间的间隔称为分离边缘,用ρ表示。支持向量机的目标是找到一个分离边缘最大的超平面,即最优超平面。也就是要确定使ρ最大时的W和b。如下图
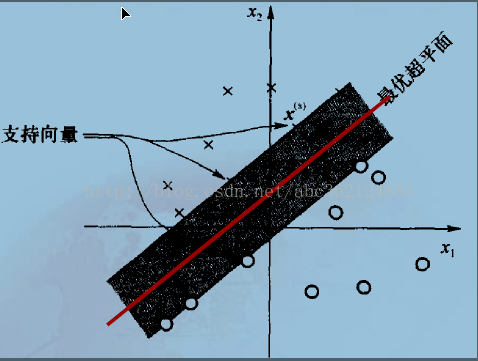
可以看出,最优超平面能提供两类之间最大可能的分离,因此确定最优超平面的权值和偏置
应是唯一的。在式(1)定义的一簇超平面中,最优超平面的方程应为:
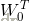
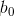
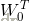
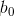
和
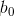
由解析几何知识可得样本空间任一点X到最优超平面的距离为
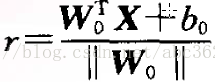
从而有判别函数 : g(X)=r ||W0||=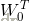
g(X)给出从X到最优超平面的距离的一种代数度量。将判别函数进行归一化,使所有样本都满足
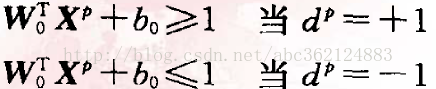
上 式中的两行也可以组合起来用下式表示
(2)
则对于离最优超平面最近的特殊样本Xs满足:I g(Xs) I=1,称为支持向量。由于支持向量最靠近分类决策面,是最难分类的数据点,因此这些向量在支持向量机的运行中起着主导作用。
可导出从支持向量到最优超平面的代数距离为
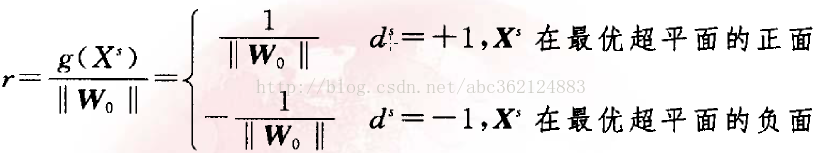
因此,两类之间的间隔可用分离边缘表示为
上式表明,分离边缘最大化等价于使权值向量的范数|| W||最小化。因此,满足式(2)的条件且使||W||最小的分类超平面就是最优超平面。
建立最优分类面问题可表示成如下的约束优化问题,即对给定的训练样本{(X1,d1),(X2,
d2),…,(Xp,
),…(Xp,
)},找到权值向量W和阈值B的最优值,使其在式(2)的约束下,有最小化代价函数
该约束优化问题的代价函数是W的凸函数,且关于W的约束条件是线性的,因此可用高等数学中Lagrange系数方法解决约束最优问题(即求解条件极值问题)。引入Lagrange函数如下
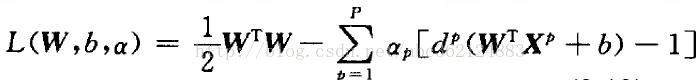
式中αp≥0,称为Lagrange系数。式中的第一项为代价函数 φ(w),第二项非负,因此最小化φ(w)就转化为求Lagrange函数的最小值。观察Lagrange函数可以看出,欲使该函数值最小化,应使第一项φ(w)↓,使第二项↑。为使第一项最小化,将上式对W和b求偏导,并使结果为零
可导出最优化条件:
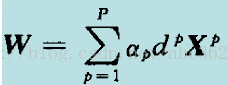
为使第二项最大化,将式(3)展开如下
将最优化条件代入上式整理得关于α的目标函数为Q(α) =L(W,b,α)
以上为不等式约束的二次函数极值问题(Quadratic Programming,QP)。由Kuhn Tucker定理知,式(3)的最优解必须满足以下最优化条件(KKT条件)
上式等号成立的两种情况:一是αp为零;另一种是 (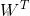
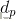
即最优超平面的权向量是训练样本向量的线性组合,且只有支持向量影响最终的划分结果,如果去掉其他训练样本重新训练,得到分类超平面相同。但如果一个支持向量未能包含在训练集内时,最优超平面会被改变。利用计算出的最优权值向量和一个正的支持向量,可)进一步计算出最优偏置
求解线性可分问题得到的最优分类判别函数为
在上式中的P个输入向量中,只有若干个支持向量的Lagrange系数不为零,因此计算复杂度取决于支持向量的个数。对于线性可分数据,该判别函数对训练样本的分类误差为零,而对非训练样本具有最佳泛化性能。








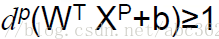

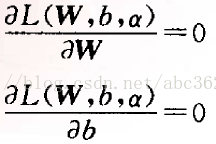
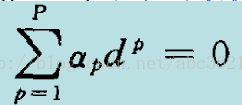
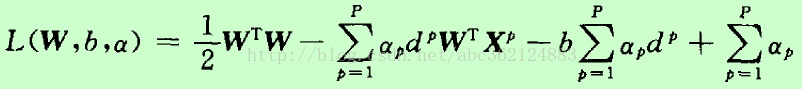
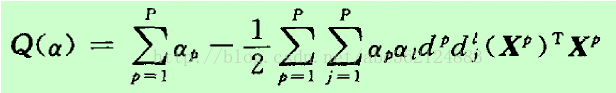

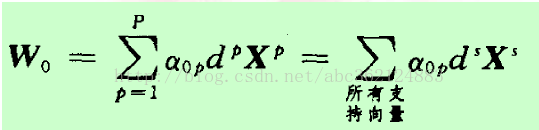
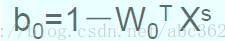
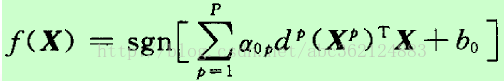













 518
518











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








