斯坦福公开课Machine Learning笔记(二)--Classification and Logistic Regression

斯坦福公开课Machine Learning笔记(二)–Classification and Logistic Regression

这系列笔记其实已经手写好, 现在一次性发上来, 主要是怕丢. 内容以Andrew Ng的讲义为主,主要以公式推导与理解为主,引入和介绍省略.对于最后的Reinforcement Learning部分, 由于没有讲义以及对其实在不熟悉, 就没有笔记了(主要还是因为没有讲义).

1. Logistic Regression

线性回归比较适合预测的问题,对于分类问题,Logistic Regression用的就非常广泛了.

训练集:
$X=\{x^{(1)},x^{(2)},...,x^{(m)}\}$
$y=\{y^{(1)},y^{(2)},...,y^{(m)}\}$, $y\in\{0,1\}$
LR其实是在线性回归的基础上再加上一个非线性函数$sigmoid$ 函数,让其更好的适应分类问题,其函数图象如下:

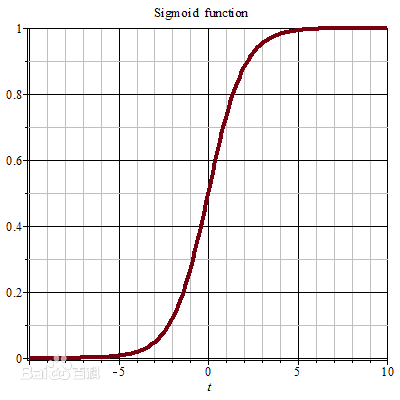
$\therefore LR的预测函数为:$

$$h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$$
其中 $g(z)=\frac{1}{1+e^{-z}}$
当 $z\to+\infty$时, $g(z)=1$, 当 $z\to-\infty$时, $g(z)=0$
$\therefore g(z)$ 可以看做是概率,可以比较好的适应分类问题.
$\therefore P(y=1|x;\theta)=h_\theta(x)$
$P(y=0|x;\theta)=1-h_\theta(x)$
$\therefore P(y|x;\theta)=h_\theta^y(1-h_\theta)^{1-y}$
$\therefore 似然函数:$
$$\begin{align} L(\theta)&=P(\vec y|x;\theta)\\ &=\prod_{i=1}^m{}P(y^{(i)}|x^{(i)};\theta)\\ &=\prod_{i=1}^m{h_\theta^y(1-h_\theta)^{1-y}}\\ \end{align}$$
$\therefore 对数似然函数:$
$$\begin{align} l(\theta)&=\log{L(\theta)}\\ &=\sum_{i=1}^m{(y^{i}\log{h_\theta(x^{(i)})+(1-y^{(i)})\log{(1-h^\theta(x^{(i)})}))}}\\ \end{align}$$
然后可以使用梯度下降法或者随机梯度下降法优化问题:
$$\theta_j:=\theta_j-\alpha \frac{\partial}{\partial \theta_j}l(\theta)$$
其中:
$$\begin{align} \frac{\partial}{\partial \theta_j}l(\theta)&=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})\frac{\partial}{\partial \theta_j}g(\theta^Tx)\\ &=(y\frac{1}{g(\theta^Tx)}-(1-y)\frac{1}{1-g(\theta^Tx)})g(\theta^Tx)(1-g(\theta^Tx))\frac{\partial}{\partial \theta_j}\theta^Tx\\ &=(y(1-g(\theta^Tx))-(1-y)g(\theta^Tx))x_j\\ &=(y-h_\theta(x))x_j\\ \end{align}$$
$\therefore \theta_j:=\theta_j-\alpha(y^{(i)}-h_\theta(x))x_j^{(i)}$

2. The perceptron learning algrithm

感知器算法与LR类似,同样是在线性上加上一个非线性的函数,但是比LR简单.

$$g(z)=\begin{cases} 1 & z \geq 0 \\ 0 &z<0 \end{cases}$$
再简单列出迭代函数:
$$\theta_j:=\theta_j-\alpha(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$

3.Another algorithm for optimizing (牛顿法)

这里Ng没有讲的特别详细,主要讲解了牛顿法的思想以及推广.
牛顿法:

$$\theta:=\theta-\frac{l^{'}(\theta)}{l^{''}(\theta)}$$

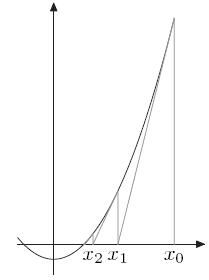
其基本思想就是：
最优化问题中，可以令 $f^{'}(x)=0$，这样可以求得极大极小值。举个栗子，上图就是 $f^{'}(x)$ 的图像。然后通过某个点的导数，快速得到 $f^{'}(x)=0$ 的点。 其实就是通过二阶导数来快速得到 $f(x)$ 的极值。
而使用泰勒展开式展开到二阶：
$f(x+\Delta x)=f(x)+f^{'}(x)\Delta x+f^{''}(x)\Delta x^2$
当且仅当 $\Delta x$无限趋向于0时成立。
$\therefore f^{'}(x)\Delta x+f^{''}(x)\Delta x^2=0$ 与上式等价。
$\therefore \Delta x=-\frac{f^{'}(x)}{f^{''}(x)}$
$\therefore \theta:=\theta-\frac{l^{'}(\theta)}{l^{''}(\theta)}$

以上是二维的情况，推广到高维：
$\theta:=\theta-H^{-1}\frac{\partial}{\partial \theta}l(\theta)$
其中$H_{ij}=\frac{\partial^2l(\theta)}{\partial \theta_i \partial \theta_j}$

牛顿法与梯度下降法相比，收敛会快很多，毕竟是通过二阶导数来求极值。但是计算代价要高很多，因为要计算$H$ 和 $H^{-1}$