0) 引论
正如名字divide and conquer所言,分治算法分为两步,一步是divide,一步是conquer。
Divide:Smaller Problems are solved recursively except base cases.
Conquer:The solution to the original problem is then formed from the solutions to the sub-problem.
说白了,分治算法就是把一个大的问题分为若干个子问题,然后在子问题继续向下分,一直到base cases,通过base cases的解决,一步步向上,最终解决最初的大问题。分治算法是递归的典型应用。
1) 分治排序的运行时间问题
这里写下这个结论只是为了后面分析时间问题的方便。
2) 最近点问题
假设在坐标平面上分布了一系列的点,那么问题是求取这些点两两之间的最短距离。
最naive的做法当然是穷举法,计算所有的两两点间的距离,然后取最小值。穷举法对于小样本总是不错的。但是对于大样本来说,就不是那么合适了,这里我们用divide-and-conquer算法来解决这一问题。
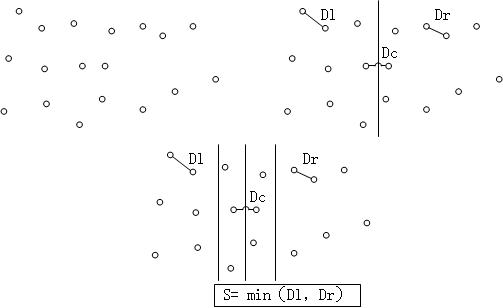
首先对于所有的点,按照x坐标将其分为两部分,这就是divide,那么最短距离就是左边部分中的最短距离Dl,右边部分的最短距离Dr,以及左右部分之间的距离Dc。对于Dl以及Dr,可以递归的计算得到,这就是conquer。那么唯一的问题就是Dc。我们知道如果最短距离是Dc的话,那么Dc<=min(Dl,Dr)。因此我们只需要计算距离divide分割线S = min(Dl,Dr)的点就可以了。进一步我们可以看到对于每个在2S区域内的点,只需要计算y坐标距离这一点不大于S的点就可以,这样可以进一步简化运算量。
for(i=0;i<NumPointsInStrip;i++)
for(j=i+1;j<NumPointsInStrip;j++)
if(Pi and Pj coordinates differ by more than S)
break;
else
if(Dist(Pi,Pj)<S)
S = Dist(Pi,Pj);
 分治算法与最近点问题
分治算法与最近点问题





 本文介绍了分治算法的基本概念及其在排序问题中的应用,并详细解析了如何使用分治算法解决最近点问题,即在二维平面上找到两点间距离最小的一对。
本文介绍了分治算法的基本概念及其在排序问题中的应用,并详细解析了如何使用分治算法解决最近点问题,即在二维平面上找到两点间距离最小的一对。
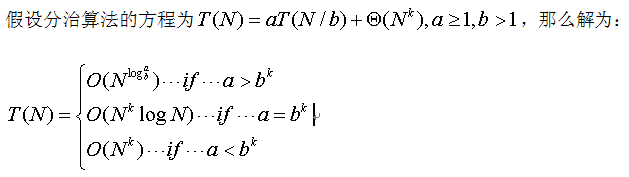
















 979
979

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








